文章目录
目录
1.引言
Quaternion(四元数)是一种三维空间旋转的表示方法,四元数由一个实部和三个虚部构成,写如
![]()
其中 i, j, k 为虚部的三个基:
![]()
不是所有的四元数对于基的关系的定义都是一致的,下文描述两种定义形式:Hamilton & JPL,它们的区别及影响。
2.Hamiltion定义
![]()
ijk=−1
四元数转换为旋转矩阵MatJPL
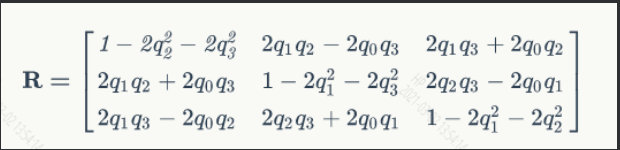
左四元数 - 乘积矩阵(left-quaternion-product matrices)

3.JPL定义
![]()
ijk=1
四元数转换为旋转矩阵MatJPL
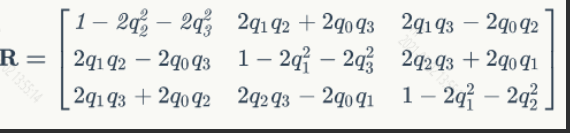
左四元数 - 乘积矩阵(left-quaternion-product matrices)
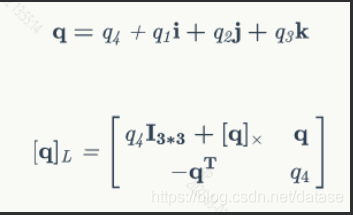





 本文介绍了四元数作为三维空间中旋转的一种表示方法,并详细对比了Hamilton与JPL两种不同的定义方式及其对旋转矩阵的影响。
本文介绍了四元数作为三维空间中旋转的一种表示方法,并详细对比了Hamilton与JPL两种不同的定义方式及其对旋转矩阵的影响。
















 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








