基于奇异函数的付款折扣模型

基于奇异函数的综合现金流模型。II：可行的及时付款折扣情景

摘要

准确比较正常现金流与折扣现金流情景下的余额，是项目参与者决定是否提供或接受及时付款折扣的关键。该决策需要确定可接受的利率和期限。这些数值通过使用奇异函数的综合现金流模型进行计算。奇异函数作用于有限范围，非常适合用于金融现象的建模。本文推导出一种信号函数，用于表达不同的付款情景，并考虑资金的时间价值。本研究对知识体系的贡献包括以下几点：（1）该模型能够准确且高效地计算余额；（2）新方法从收款人和付款人的角度评估了折扣的可行范围，并通过工程经济分析加以验证；（3）提供了一种使用新型列线图进行决策的简化流程，使项目参与者能够找到互利的付款安排。

DOI: 10.1061/(ASCE)CO.1943-7862.0000906。© 2014 美国土木工程师学会。

作者关键词：现金流；即时付款折扣；列线图；奇异性函数；成本与进度。

引言与依据

现金流管理被认为是建筑行业成功的关键（肯利 2003）。然而，流动性不足是实现正向现金流的巨大障碍，尤其对于难以获得银行融资的小型和初创企业而言（Kouvelis 和 Zhao 2012）。在零售业，“零售商和供应商都:::需要短期融资”（Kouvelis 和 Zhao 2012，第566页），因此采用贸易信贷。建筑业中的大多数材料供应商也愿意提供即时付款折扣（Cui 等，2010）。代码2/10，净30表示，如果付款方在10天内支付账单，则收款人将给予账单金额2%的折扣；否则付款方须在30天内支付全额（否则可能产生滞纳金）。本文中所有天数均为日历日，因为利息在周末也累计。从这一意义上讲，这是一种会计机制，允许在短期内付款时减少账单金额，从而为改善现金流提供了宝贵机会。

此类信用在联邦采购条例（FAR）中被称为即时付款折扣，该条例由总务管理局、国防部和国家航空航天局联合发布，并将其定义为“承包商为在到期日前付款而提供的发票金额减免” （GSA 2005，第32.9‐1页）。对于政府采购，合同官员应“尽最大努力获得商业折扣和即时付款折扣”（ GSA2005，第13.1‐3页）。尽管FAR敦促利用折扣，其关于施工合同的条款—52.232‐26（固定价格建筑师‐工程师合同的及时付款）和52.232‐27（施工合同的及时付款）—并未提供此类折扣应如何构成的具体细节。仅要求正确的发票应列出“交货和付款条款（例如，即时付款折扣条款）”（GSA 2005，第52.2‐222页）。此外，管理和预算办公室强调“随着政府稳步进入电子商务主流，如果允许各机构在对政府有利时提前付款，它们将越来越有可能实现效率提升和成本节约”（OMB 1999，第52582页），但在第1315.2 节中明确将施工合同单独列出，并在第1315.14节中提供了更详细的付款要求。最后，对于政府的信用卡支付，第 1315.17节提供了公式及简单示例，用于将任何即时付款折扣与美国财政部公布的每日复利资金现值进行比较。州政府也有折扣规定；然而，许多州并未特别提及施工合同。例如，西部州合同联盟（WSCA2012），作为全国州采购官员协会的一个分支机构，代表15个州，鼓励报价中包含即时付款折扣。尽管许多州在合同授予决策中不考虑30天以内的折扣，但许多州明确规定施工合同付款应在30天内完成，而不是 45天。它们还鼓励充分利用所提供的任何折扣，例如加利福尼亚州（1999）、德克萨斯州（2001）和马萨诸塞州（2011）。

提前付款折扣与不平衡报价（例如前期加载）具有类似的效果，即增加了项目早期的现金流入，但不同之处在于金额略有减少，并且——与不平衡报价不同——不会操纵单价。它激励在完成部分工作后及时付款，从而支持商业交易中的公平性，因为—不同于不平衡报价—“承包商不应被要求亏本完成工作，而业主也不应为任何一项支付超过合理利润的金额”“承包商不应被要求亏本完成工作，而业主也不应为任何一项支付超过合理利润的金额”（格兰斯伯格和里默2009，第1,140页）。因此，本研究面临的挑战是深入探讨这种公平性可以从数学上进行建模，以支持实践实施。要在收款人和付款人之间实现任何折扣，必须从双方的角度进行分析，并且必须存在双赢情景。通常，当付款人发出采购订单时，“充分利用所有现金折扣或提前付款折扣是明智的”（Zwick 和 Mille 2004，第247页）。然而，如果该付款人决定接受折扣，“他将材料付款计划提前”，“这种前期支付做法会通过增加透支余额而对项目的财务状况产生不利影响”（Cui 等，2010，第366页）。但从收款人的角度来看，Hill 和 Riener（1979，第69页）认为：“企业不希望提供更大的折扣，因为采用折扣政策后的现金流现值将少于当前政策下的现值。” 因此，迫切需要在这些截然相反但可能重叠的立场之间找到一种数学共识。更具体地说，需要一种明确的方法来帮助建筑行业的决策者判断是否应提供（从收款人角度）或接受（从付款人角度）此类折扣，以及理想的折扣比率和期限是多少，而不是仅仅依赖传统做法并应用 2=10，净30。

为保持一致性，在以下各节中使用术语“收款人”和“付款人”，而非“承包商”，因为后者意味着同时承担两种角色——从业主处收款并向分包商付款。

文献综述

现有提前付款折扣研究的不足之处

在付款折扣研究中，Hill 和 Riener（1979）提出了一种方法，从零售市场中收款人’的角度计算最高和最优折扣率。他们的理论基于以下假设：部分销售将享受折扣付款，但其余部分则按全价支付。通过比较正常（无折扣）和折扣情况下的现金流的净现值，在该情景下，收款人可以制定出合理的信用政策。然而， Hill和Riener（1979）的假设基于零售企业，其市场环境与建筑行业的收款人和付款人不同。Ng等（1999）调查了来自不同行业的950家企业，发现信用政策的目标包括：（1）在付款前提供检查货物的时间；（2）通过付款方是否接受折扣来评估付款方的信用状况；（3）建立一种依赖关系（从而形成付款人对收款人的商业忠诚度）；（4）建立付款人良好的财务声誉。这取决于收款方的规模，因为大型企业更容易为其个别付款方实施复杂的信用政策。Kouvelis和Zhao（ 2012）应用博弈论对供应商与零售商之间的战略互动进行建模，并从供应商的角度确定最优贸易信贷。然而，他们关于 “一个供应链中供应商向面对不确定需求的新闻报童式零售商销售”的假设（Kouvelis 和 Zhao 2012，第566页）并不适用于建筑行业，在建筑行业中，“项目的全部范围[是]在图纸和规范中明确定义的”（Zwick和Miller 2004，第 245页），且需求的不确定性更小。尽管如此，他们的研究展示了一种可行的方法，即综合考虑收款人和付款人的观点，比较企业自有资金与银行贷款融资的选择，并优化折扣参数。

在施工管理领域，de la Garza和Melin（1986）主张施工合同应允许预付款以缓解通货膨胀的影响。Touran等（2004）测试了美国交通部的历史和更新的及时付款条款如何影响承包商利润。然而，他们的研究仅聚焦于交通项目的保留金释放。崔等（2010）将系统分析应用于现金流管理策略，并在其模型中引入材料支付模块以评估不同的支付政策。然而，折扣决策的数学原理仍未被探索。Al‐Hussein等（2013）对建筑行业的折扣进行了建模，并分别描述了付款人和收款人视角下的最低折扣和最高折扣。然而，该研究并未得出全面的理论决策过程。总体而言，迫切需要深入研究建筑行业的折扣问题，并推导出数学上严谨的原则。

及时付款情景分析的研究问题

研究问题可划分为以下几点：（1）对于是否提供或接受折扣的决策，必须比较相反情景（提供或不提供；接受或不接受）下的余额。（2）多个因素影响可行折扣范围，包括加价率、折扣率和期限，以及提供折扣方（收款人）和接受折扣方（付款人）各自的融资费用。调整这些参数会改变现金流状况，因此有必要高效地建模其余额。（3）如果选择了折扣，则需要一种方法来检查其可行性。本文提出了升级版综合现金流模型，并将其应用于折扣问题。假设有利可图的折扣总会被接受，即范围不包含概率性影响。为实现从收款人和付款人角度确定可行的即时付款折扣这一目标，设定了三个研究目标：

1. 生成能够表达不同即时付款折扣情景的信号函数，并将合成现金流模型扩展以适应即时付款折扣条件；
2. 确定可行折扣范围，并通过工程经济分析验证该范围；
3. 定义建设项目中折扣的简单决策过程。

奇异性函数定义

奇异函数最初用于结构工程中分析作用在梁上的不同类型荷载。它们本质上是如公式（1）所定义的分段函数。尖括号指示自变量y与截止值a之间的关系：如果y小于a，则返回0；否则，将尖括号视为普通代数中的圆括号。为了实现定制化，将比例因子s和指数n引入到该项中。这些参数共同允许建模线性和非线性函数，并可在任意y值处开启或关闭。奇异函数的这些特性在施工管理领域以数学系统化方法建模多种现象时极为有用，例如线性进度计划（Lucko2009）、现金流（ Lucko 2011b）以及资源均衡（Lucko2011a）。奇异函数的一个优点是其定义简单直接，但又足够灵活，能够捕捉更复杂的模型。公式（1）项中的每个参数本身还可以包含另一个奇异函数，从而实现更强的可扩展性。当多个奇异函数项的指数和截止值相同时，可以对它们进行加减运算。所有项均可进行乘除、积分或微分操作。奇异函数的一个重要优点是，来自不同应用的基于方程的模型可以相互关联，形成一个集成的施工项目管理方法：一旦建立了线性进度计划，研究人员即可在公式（1）中引入成本斜率[参数s，将其升级为现金流模型。将成本斜率视为加价的函数，可进一步扩展模型以适应不平衡报价和前期加载方案中可能出现的不均匀加价分布情况。将生产率斜率转换为资源数量，则为执行资源均衡和资源分配提供了可能。本文未提及的更多扩展也是可行的，将在未来研究中进一步探索

$$
zðyÞ ¼ s · hy− ain ¼
\begin{cases}
0 & \text{for } y< a \
s · ðy− aÞn & \text{for } y ≥ a
\end{cases}
$$

（1）

及时付款情况下的现金流模型

综合现金流模型

如Su和Lucko（2014）中更详细讨论的，信号函数的独特之处在于它们仅在周期性信号时间被触发。其基本思想是将向下取整（floor）和向上取整（天花板）算子 bc和 de引入到 公式(1)基本项中的自变量y。该函数仅在经过取整操作后的 y大于截止值a时才被激活，因为算子 bc会将y向下取整到前一个整数，而 de算子则会将其向上取整到下一个整数，因此这些项的组合仅在y的有限范围内起作用。例如，hbyc− 2i1从2.0开始激活，并由于取整操作产生阶梯状的z值；而 hdy e− 3i1从2.000…1开始激活，同样呈现阶梯状。将这两个项相减后，会在整数y ¼ f2, 3, 4, … g处精确产生一个单位信号，而在其间的所有实数上为零。此类周期性表达式可用于对现金流中的周期性财务事件（如收款和计息）进行建模。若与指数中的另一个奇异函数结合，可实现周期性的复利利息也可以被建模。将所有付款的未来值相加，并减去所有成本的未来值，从而得到任意时刻含利息的余额的综合方程，该方程被称为综合现金流模型。

信号函数在即时付款折扣情景中的应用

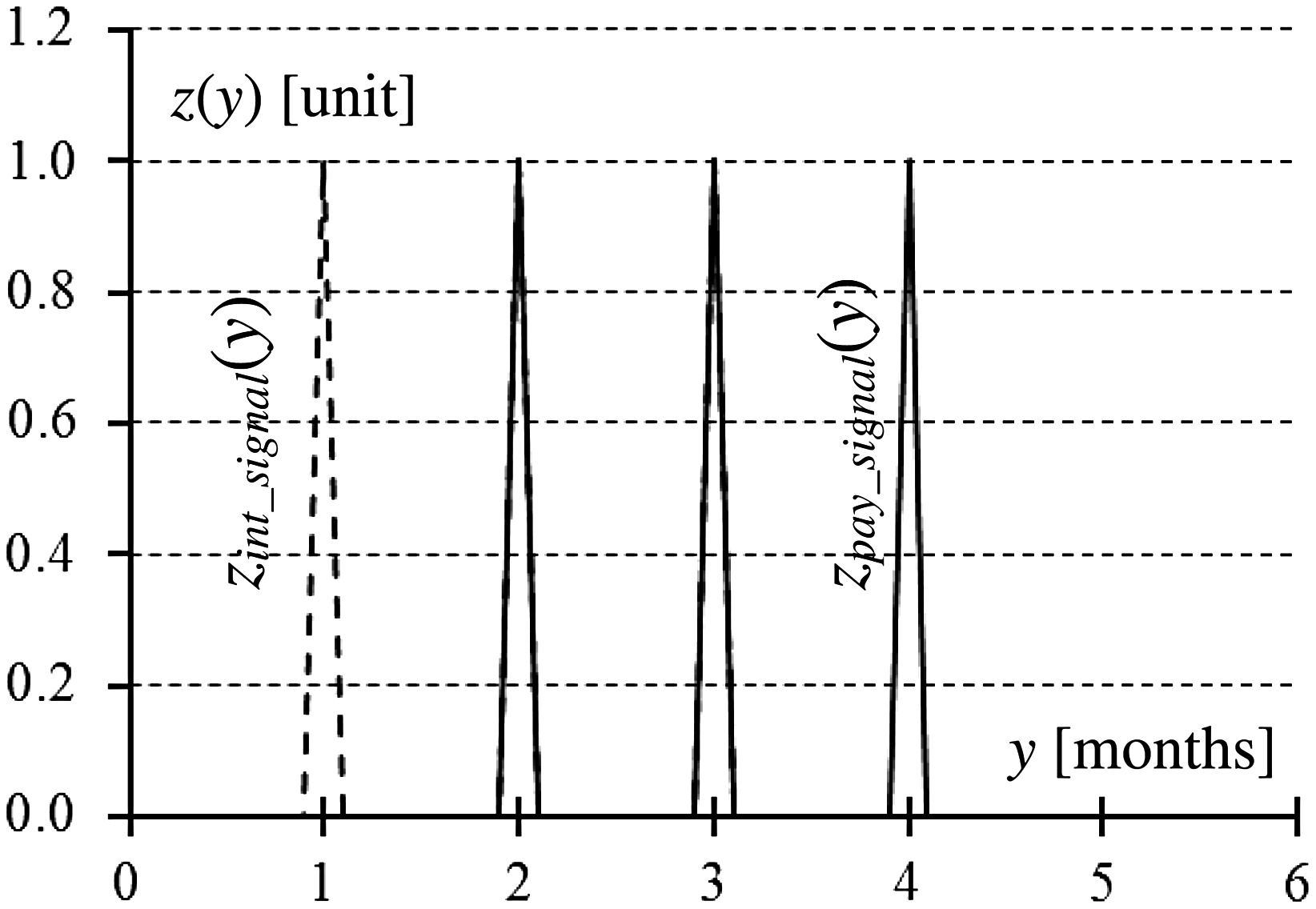
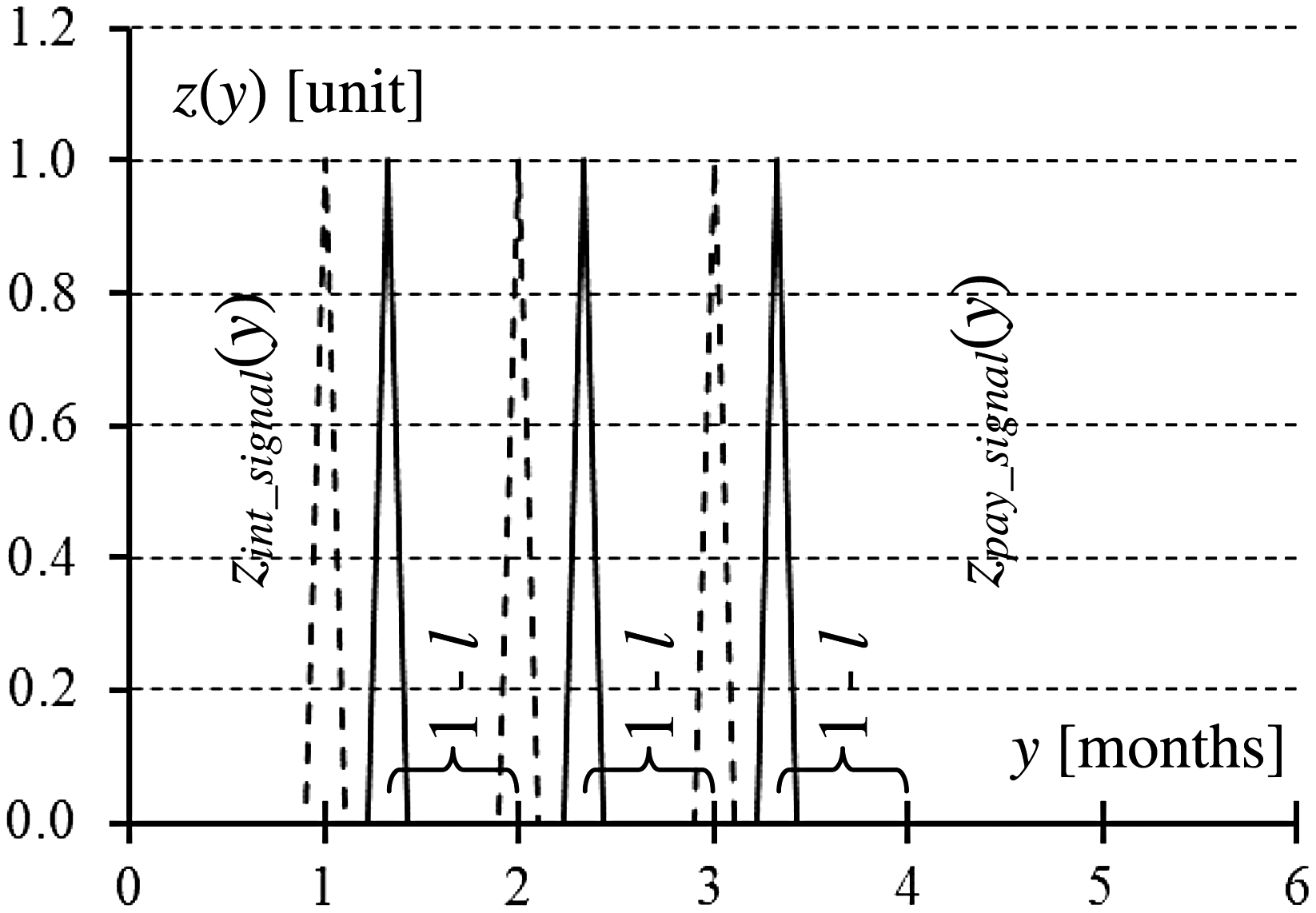
为了模拟周期性现金流，假设示例1中活动在时间零点开始，持续期限为3个月。在正常付款情景下，根据图1，利息在每月末收取，并在账单发出后1个月的延迟后收到付款。然而，根据图2，收款人提供一个 2=10，30天内付款可享受折扣的及时¯付款方案 l ¼ 0。3个月，折扣率为 ρ ¼ 2%。图1和2中的纵轴为单位信号（本文中为二进制）。计息信号用虚线表示，而付款信号用实线表示（在图–4中，图1的两条信号线在时间2至4重叠）。享受折扣会使信号正确地比正常付款情景下的期末信号1−l个时期更早。由于计息不受收款时间影响，因此两种情景下的利息信号保持不变。公式(2)是及时付款情景下的信号方程

$$
zpay\ signal ¼ s · ½hby þ 1− lc−ða S þ bÞi1
− hby þ 1− lc−ða F þ bÞi1
− s · ½hdy þ 1− le−ða S þ bþ 1Þi1
− hdy þ 1− le−ða F þ bþ 1Þi 1
$$

（2）

公式（3）中每笔付款的现值将成本斜率通过增加利润加价 M并减去折扣 ρ 转换为账单斜率，时间依据付款信号

函数。式(4)将其转换为付款的累积未来值，将其可能存在的大量中间项简化为类似于年金的未来值的简洁表达式。控制项hy−ð:::Þi0用于利息因子的指数中，以确保付款（现在可能相对于图2中的利息移动了(1− l)）在每个周期结束时被正确复利计算。式(5)随后计算及时付款情景的余额。本文推导出的成本和利息方程与Su和Lucko（2014）中列出的相同。式 (2)正确地对即时付款折扣信号进行建模，根据式(4)将其转换为折现付款的未来值，并根据式(5)生成新的余额模型

$$
zeach\ payðyÞ ¼ C
Dþ d2 · ð1 þ MÞ · ð1− ρÞ · zpay\ signalðyÞ
$$

（3）

$$
zFV\ disc\ pay ¼zeach付款ðba Scþl ＋bÞ· ð1＋利率 iÞhbyc−ðba Sc＋b＋1Þi1
· hy−ðba Sc＋ l＋ bÞi0 · ð1＋ iÞ（1−l）·hy−ðba Sc＋b＋1Þi0
þ zeach\ payðba Sc＋ l＋ b＋ 1Þ · 1i ·½ð1＋ iÞhbyc−ðba Sc＋ b＋1Þi1
−ð1＋ iÞhbyc−ðda Fe＋ b−1Þi1 ·ð1＋ iÞ（1−l）·hy−ðba Sc＋ b＋2Þi0
þ zeach\ payðda Fe＋ l＋ b−1Þ · hy−ðda Fe＋ l＋ b−1Þi0
·ð1＋ iÞ（1−l）·hy−ðda Fe ＋bÞi0
$$

（4）

$$
zbaldisc ¼ zFVdiscpayðyÞ−½zcostðyÞ ＋ zintatsignalðyÞ
$$

（5）

扩展合成现金流模型的验证

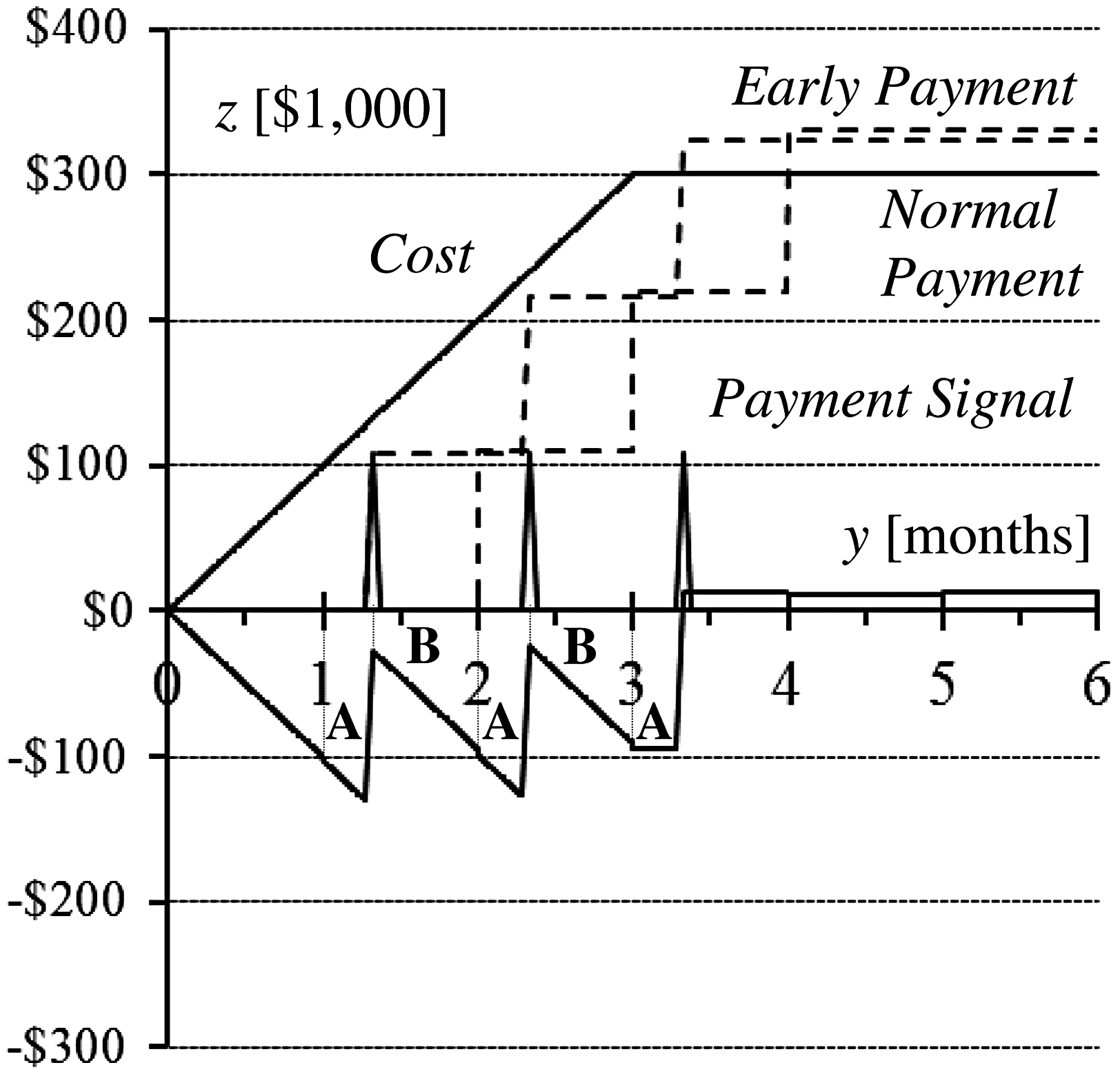
为了验证使用新的奇异函数计算及时付款情景余额的准确性，将其与Su和Lucko（2014）提出的时序余额法进行对比。后者需要三个步骤来计算月度余额：首先累加至每月末为止的累计成本，然后在一个无穷小时间段 ε内减去这些成本所产生的利息，再在另一个无穷小时间段 ε内加上付款金额。在示例2中，假设D ¼ 3个月（假设每个月为30天），C ¼300,000美元，a S ¼ 0个月，d1 ¼ 0个月，d2 ¼0个月（即aS ¼ 0个月，a F ¼ 3个月），b ¼ 1个月，i ¼ 5%=每月，M ¼ 10%的成本， l ≈ 0.33个月（或10个日历日），以及 ρ ¼ 2%。本例中的偏移 d1和延迟d2设为零，仅是为了更清晰地说明利息计算过程，但实际上可以是任意非整数值。折价付款金额为C · ð1 þ MÞ · ð1− ρÞ=ðD ＋ d 2Þ ¼ 102,479.7美元。图3显示了正常和及时付款曲线。付款信号发生在每月第10天，但利息在每月末收取。其计算区分了两个组成部分，如图3中透支区域A和B所示，并在表 1中列出。区域A在y ∈ f1; 1.33g期间包含一个矩形（前期余额）和一个三角形（新增透支）。矩形的高度为前期期末余额（表1 中的102,479.7美元）；三角形的高度为0.33个月的额外成本 （33,000美元）。必须在中间时间y ¼ 1.33 ＋ ε确定利息，但复利按0.67个月计算，仅在y ¼ 2时收取。区域B在y ¼ f1.33; 2g期间类似处理。区域B的矩形部分在y ¼ 1.33时余额为 27,679.70美元；三角形部分增加67,000美元，为期0.67个月。在y ¼ 2 ＋ ε（周期结束）时，A部分的利息（复利0.67个月）和B部分的利息被加入余额，如表1所示。在时间4处出现的一个微小利息步长，是由第3周期前10天的负余额与正余额所赚取的利息共同作用所致。

第3个期限内的最后20天，在本文中为简化起见，假设其以相同的利率赚取利息。表2将其最右列中奇异函数计算的付款和成本的未来值结果与表1的结果进行了比较。该表的成本的未来值和支付的未来值两列应用了Su和Lucko（2014）的公式(15)以及本文的公式(4)。两种余额计算方法的结果完全相同，验证了付款方案的分析，并实现了研究目标1。

表1. 使用无穷小偏移 ε 计算带利息的余额
y（月）	Cost（1,000美元）	利息（1,000美元）	付（1,款000美元）（余1,额000美元）
1	-100	0	0	-100.0000
1 ＋ ε	0	100 · 利率 i=lnð1＋利率 iÞ − 100 ¼ 2.4797	0	-102.4797
1.33	-33	0	107.8	-27.6797
1.33＋ ε	0	利率 irectangle ¼ 102.4797 · ½ð1＋利率 iÞ0.33 − 1 ¼ 1.6633 利率 itriangle ¼ 100 · ½ð1＋利率 iÞ0.33 − 1= lnð1＋利率 iÞ− 33 ¼ 0.2671 利率 iA ¼ 1.6633＋ 0.2671 ¼ 1.9304	0	-27.6797
2	-67	0	0	-94.6797
2 ＋ ε	0	利率 irectangle ¼ 27.6797 · ½ð1＋利率 iÞ0.67 − 1 ¼ 0.9197 利率 itriangle ¼ 100 · ½ð1＋利率 iÞ0.67 − 1= lnð1＋利率 iÞ − 67 ¼ 1.1071 利率 iB ¼ 0.9197＋ 1.1071 ¼ 2.0268i ¼利率 iA · ð1＋利率 iÞ0.67 ＋利率 iB ¼ 4.0214	0	-98.7011
2.33	-33	0	107.8	-23.9011
2.33＋ ε	0	利率 irectangle ¼ 98.7011 · ½ð1＋利率 iÞ0.33 − 1 ¼ 1.6020 利率 itriangle ¼ 100 · ½ð1＋利率 iÞ0.33 − 1= lnð1＋利率 iÞ − 33 ¼ 0.2671 利率 iA ¼ 1.6020＋ 0.2671 ¼ 1.8691	0	-23.9011
3	-67	0	0	-90.9011
3 ＋ ε	0	利率 irectangle ¼ 23.9011 · ½ð1＋利率 iÞ0.67 − 1 ¼ 0.7942 利率 itriangle ¼ 100 · ½ð1＋利率 iÞ0.67 − 1= lnð1＋利率 iÞ − 67 ¼ 1.1071 利率 iB ¼ 0.7942＋ 1.1071 ¼ 1.9013利率 i ¼利率 iA · ð1＋利率 iÞ0.67 ＋利率 iB ¼ 3.8325	0	-94.7336
3.33	0	0	107.8	13.0664
3.33＋ ε	0	利率 irectangle ¼ 94.7336 · ½ð1＋利率 iÞ0.33 − 1 ¼ 1.5376	0	13.0664
4	0利率 irectangle earned¼ −13.0664 · ½ð1＋ iÞ0.67 − 1 ¼ −0.4341	0	13.0664
4 ＋ ε	0	利率 i ¼irectangle · ð1＋ iÞ0.67 ＋i矩形 earned ¼ 1.1546	0	11.9118

粗体值为计息和收款后的期末余额。

表2. B使用付款和成本的未来值计算余额及利息 和成本
y（月）	成本的未来值（1000美元）	付款的未来值（1000美元）	余额（1,000美元）
1	100 · ½ð1＋利率 iÞ1 − 1=lnð1＋利率 iÞ ¼ 102.4797	0.00	-102.4797
1.33	102.4797＋ 33 ¼ 135.4797	107.8	-27.6797
2	100 · ½ð1＋利率 iÞ2 − 1=lnð1＋利率 iÞ ¼ 210.0833	107.8 · ð1＋利率 iÞ0.67 ¼ 111.3822	-98.7011
2.33	210.0833＋ 33 ¼ 243.0833	111.3822＋ 107.8 ¼ 219.1822	-23.9011
3	100 · ½ð1＋利率 iÞ3 − 1=lnð1＋利率 iÞ ¼ 323.0671	111.3822 · ð1＋利率 iÞ1 ＋ 107.8 · ð1＋利率 iÞ0.67 ¼ 228.3335	-94.7336
3.33	323.0671	228.3335＋ 107.8 ¼ 336.1335	13.0664
4	323.0671 · ð1＋利率 iÞ1 ¼ 339.2205	111.3822 · ð1＋利率 iÞ2 ＋ 111.3822 · ð1＋利率 iÞ1 ＋107.8 · ð1＋利率 iÞ0.67 ¼ 351.1323	11.9118

表3. 收款人和付款人策略
策略	时间	金额	结果
收款人	更早	More	None
付款人	稍后	Less	None
收款人	更早	Less	交易（折扣）
付款人	稍后	More	交易（罚金）
## 可行的及时付款折扣
可行折扣定义为对收款人和付款人都有利的折扣。收款人和付款人的观点之间存在根本差异。双方均采用默认的财务策略，即尽可能延迟现金流出并提前现金流入，这种策略仅在个体层面合理，但在双方互动中则相互矛盾。收款人希望更早且更多地收到款项，而付款人则希望更晚且更少地支付。然而，这种极端立场可能导致收款人和付款人无法达成交易。如表3所示，只有当一方在某一方面做出让步时，才可能达成交易，例如从收款人’的角度来看，虽然收款金额更少但收款时间更早，或从付款人’的角度来看，虽然支付金额更多但支付时间更晚。后者可能涉及迟延付款罚金，这在概念上与及时付款折扣相反，不在本文讨论范围内，将在未来研究中探讨。关于双方的互动，从收款人’的角度来看，折扣应确保提供折扣比不提供更有利可图；而从付款人’的角度来看，则应反过来确保接受折扣比不接受更有利可图。只有当这两个条件都满足时，折扣才有可能被执行，即能够达成交易。只有当收款人的银行利率低于付款人的银行利率时，才可能存在可行的折扣范围，其中部分或全部收益可由该付款人共享。以下章节将探讨收款人和付款人目标重叠区域的下限和上限（保底与封顶折扣）。

下限（保底折扣）

付款人的观点决定了折扣的下限，因为如果付款人拒绝接受，无论收款人提供的优惠多么优厚，该方案都不可行。理性付款人将比较接受与不接受折扣时的现金流。接受折扣意味着付款人更早但金额更少地付款，这实质上将付款人的现金流出提前，并相应改变其余额。理论上，提供折扣的收款人应了解付款人的现金流出和流入情况，从而计算出付款人的余额。然而，这种情况几乎从未发生。因此，收款人必须处理这种次优情况：除非及时付款的未来值小于正常付款的未来值，否则付款人不会接受折扣。不过，即使在次优情况下，仍可计算出折扣的下限。本文通过使用付款人的融资利率 $i_{payer}$，比较正常付款和及时付款情景的未来值，其中正常付款依据 Su和Lucko（2014）的公式(13)，及时付款依据本文的公式(4)。收款人可通过多种方式评估付款人的融资利率：直接询问、向银行咨询，或根据公开的财务报告或付款人曾接受过的折扣进行推测。如果 $zFV_{disc\ pay}(da \cdot Fe + b) \leq zFV_{pay}(da \cdot Fe + b)$，则在时间 $y = da \cdot Fe + b$ 的折价付款的未来值小于正常付款的未来值，即付款人应当接受该折扣。因此，$\rho$ 的下限（保底折扣）为 $1–(1 + i_{payer})^{l–b}$，如公式 (6)所示。

$$
zFV_{disc\ pay}(da \cdot Fe + b) \leq zFV_{pay}(da \cdot Fe + b)
\Rightarrow \frac{C}{D+d_2} \cdot (1+M) \cdot (1-\rho) \cdot (1+i_{payer})^{b-l}
\leq \frac{C}{D+d_2} \cdot (1+M)
\Rightarrow (1-\rho) \cdot (1+i_{payer})^{b-l} \leq 1
\Rightarrow \rho \geq 1-(1+i_{payer})^{l-b}
\Rightarrow \rho_{floor} = 1-(1+i_{payer})^{l-b}
$$

（6）

为验证，“比较不同付款方案对承包商的经济价值是有帮助的。该技术利用工程经济学，基于资金的时间价值来评估经济计划和策略的价值”（Halpin和Woodhead 1998，第125页）。在示例3中，分包商（收款人）为总承包商（付款人）工作。在正常付款情景下，账单在1个月后支付。收款人提供ρ=l，净b的正常付款$C \cdot (1 + M)$，其参数包括及时付款期 $l$（月）、折扣 $\rho$（账单百分比）、计费到付款延迟 $b$（月），以及付款方利率 $i_{payer}$（%/月）。图4展示了两种与即时付款折扣相关的实际情景：收款人提供折扣且付款人接受折扣，如图4(a)所示；或收款人不提供折扣，付款人无法享受折扣，如图4(b)所示。另外两种情景仅存在于假设中：提供但不接受，或未提供但希望接受。前者无关紧要，后者不可能发生，且两者的结果均与图4(b)相同。图 4(a)中的上方时间轴表示从收款人视角的现金流，下方时间轴表示从付款人视角的现金流。垂直箭头指向时间轴表示现金流入，远离时间轴表示现金流出。两个时间轴之间的箭头表示从付款人向收款人（本文中为清晰起见，不考虑保留金）。虚线箭头表示实际发生的实线箭头对应的未来值。在图4(a)的及时付款情景中，付款人时间轴上方的箭头表示付款人现金流出（及收款人现金流入）的资金时间价值。若在时间$l$付款，则付款金额为 $C \cdot (1 + M) \cdot (1− \rho)$；否则在月末付款金额为 $C \cdot (1 + M)$。这相当于收款人为付款人提供了一笔具有隐含利率的融资。“该利率即买方放弃折扣以换取额外20天融资机会所付出的机会成本”（Ng等，1999，第1页，110行）。因此，$C \cdot (1 + M)$也是 $C \cdot (1 + M) \cdot (1− \rho)$在折扣期内按复利计算的未来值。公式(7)根据折扣参数计算隐含利率。当然，只有当隐含利率高于该期限内的融资利率时，享受折扣才是经济的。图4(a)中时间轴下方的箭头将此情况与通过银行贷款融资以享受折扣的情形进行了比较。在图4(b)的正常付款情景中，付款人不享受折扣，而是进行融资（即将资金直接支付给收款人）。假设所有付款均可快速、便捷地完成，且费用极低甚至免费，例如电汇或电子交易。为简洁起见，未考虑支票邮寄和存入的情况。

$$
C \cdot (1− \rho) \cdot (1 + i_{implicit})^{b−l} = C
\Rightarrow \rho = 1−(1 + i_{implicit})^{l−b}
\Rightarrow i_{implicit} = (1− \rho)^{1/(l−b)} − 1
$$

（7）

理性付款人将根据公式（8）进行分析，以比较两种情景的盈利能力。比较必须在周期结束时进行：采取折扣所获得利润的未来值，等于两种情况下贴现付款未来值之差，即按隐含利率复利与按融资利率复利之间的差额。而不采取折扣的利润当然为零，因为付款人需为$C \cdot (1 +M)$融资，假设需要银行贷款。根据公式（8）， $\rho$的下限（保底折扣）为 $1−(1 + i_{payer})^{l − b}$，该结果与公式（6）相同，而该式是从合成模型推导得出的。此结果表明，付款人的利率影响折扣下限。这意味着保底折扣代表了折扣可行域的下限：即在此数值时，付款人对是否接受折扣持无差异态度。将式（7）代入式（8）得到式（9），该式表明当隐含利率超过财务利率时，享受折扣是合理的。

$$
profit_{take\ discount} \geq profit_{not\ take\ discount}
\Rightarrow \rho_{floor} = 1−(1 + i_{payer})^{l−b}
$$

（8）

$$
\rho \geq 1−(1 + i_{payer})^{l−b}
\Rightarrow 1−(1 + i_{implicit})^{l−b} \geq 1−(1 + i_{payer})^{l−b}
\Rightarrow i_{implicit} \geq i_{payer}
$$

（9）

上限（封顶折扣）

本节的方法类似于之前描述的保底折扣分析。从收款人的角度决定折扣的上限，因为如果收款人拒绝提供该折扣，则无论付款人多么希望，该方案都是不可行的。理性收款人将比较提供折扣与不提供折扣情况下的现金流。必须使用收款人的融资利率，根据Su和Lucko（2014）的公式(19)（用于计算正常余额）以及本文的公式(5)，比较正常付款和及时付款情景的未来值。如果$zbal(da \cdot Fe + b) \leq zbal_{disc}(da \cdot Fe + b)$，则在时间$y = da \cdot Fe + b$处，正常付款的未来值小于折价付款在同一时刻的未来值——前提是付款人接受了该折扣。因此，本文所称的最高折扣即为上限，其值为 $\rho =1−(1 +i_{payee})^{l−b}$，见公式(10)。

$$
zbal_{disc}(da \cdot Fe + b) \geq zbal(da \cdot Fe + b)
\Rightarrow zFV_{disc\ pay}(da \cdot Fe + b) \geq zFV_{pay}(da \cdot Fe + b)
\Rightarrow \rho \leq 1−(1 + i_{payee})^{l − b}
\Rightarrow \rho_{ceiling} = 1−(1 + i_{payee})^{l − b}
$$

（10）

工程经济学再次用于验证此结果。图4(a和b) 表示提供或享受折扣与否。在图4(a)中，付款人进行折价付款。成本在$C \cdot (1 + i_{payee})^l$期间复利至时间$l$，此时付款$C \cdot (1 + M) \cdot (1–\rho)$减少了余额。利润的未来价值在此情景下，利润的未来价值是成本的未来值与付款的未来值之间的差额。在图4(b)中，付款人进行正常付款。成本按 $C \cdot (1 +利率\ i_{payee})^b$复利计算一个完整期限，利润的未来价值为成本的未来值与付款的未来值之差，$C \cdot (1 + M)$。理性收款人将根据公式（11）进行分析，以在时间 $b$ 比较两种情景的盈利能力。根据公式（11）， $\rho$的上限（封顶折扣）为 $1−(1 +利率\ i_{payee})^{l−b}$，该结果与从合成模型推导出的公式（10）相同。此结果表明，收款人的财务利率影响折扣的上限。这意味着最高折扣代表了可行折扣区域的上限：即在此值时，收款人对是否提供折扣无差异（Al‐Hussein 等, 2013）。

$$
profit_{take\ discount} \geq profit_{not\ accept\ discount}
\Rightarrow [C \cdot (1 + M) \cdot (1− \rho)− C \cdot (1 + i_{payee})^l] \cdot (1 + i_{payee})^{b−l}
\geq C \cdot (1 + M)− C \cdot (1 + i_{payee})^b
\Rightarrow \rho \leq 1−(1 + i_{payee})^{l−b}
\Rightarrow \rho_{ceiling} = 1−(1 + i_{payee})^{l−b}
$$

（11）

根据公式(12)，可行折扣的充分条件是最低折扣小于最高折扣。换句话说，只有当付款人的利率 $i$ 低于收款人的利率 $i$ 时，他们的可行折扣范围才不是空集 ∅。否则，双方无法就折扣达成协议。在示例4中，假设付款人的利息为5%/月，但收款人的利息为7%/月，且折扣条件为 $\rho=10$，净30。根据公式(13)，可行折扣范围为{3.2003%, 4.4104%}。这些数值在后续章节中有详细说明，并通过图形进行展示。显然，传统的2/10，净30对于这两个参与者而言不是一个可行折扣。如果收款人仍想提供2%的折扣，则需将 $l$至少延长至18天，通过求解公式(13)得到 $l \approx 17.58$ 天。

$$
\rho \in {\rho_{floor}; \rho_{ceiling}} \neq \varnothing
\Rightarrow \rho_{floor} \leq \rho_{ceiling}
\Rightarrow 1−(1 + i_{payer})^{l−b} \leq 1−(1 + i_{payee})^{l−b}
\Rightarrow i_{payer} \leq i_{payee}
$$

（12）

$$
\rho \in {\rho_{floor}; \rho_{ceiling}}
\Rightarrow {1−(1 + i_{payer})^{l−b}; 1−(1 + i_{payee})^{l−b}}
\Rightarrow {3.2003\%; 4.4104\%}
$$

（13）

三级封顶折扣（扩展折扣范围)

收款人通常希望更早收到款项，并在可能的情况下获得收益。收益意味着尽管付款金额少于正常情况，但这种更早的付款将通过节省利息使余额产生净收益。提前付款曲线（图抬高）所涉及的融资金额面积小于正常付款曲线（图5中虚线和实线分别表示），因此产生的利息更少。因此，根据公式（11），存在较少的折价付款（较少流入）与较少利息（较少流出）之间的权衡。然而，只有当满足一个充分条件时，即付款人的融资利率低于收款人的融资利率，才能实现收益。此外，如果该条件得到满足，且付款人与收款人的利率水平仍然非常接近，则可行折扣范围非常狭窄（例如，示例4中的 3.2003–4.4101%）。此外，收款人和付款人可能不了解彼此的财务信息，这也使得确定和使用折扣更加困难。

如果收款人的财务状况正在恶化（例如，资金链断裂导致现金储备减少和破产威胁），收款人可能会认为更早收到款项比获得收益更为重要。在这种情况下，收款人可能会提供较大的折扣，并放弃部分加价。另一种情况在理论上是可能的，尽管可能性较小，即收款人可能 desperation 到提供非常大的折扣，不仅放弃全部加价，甚至无法覆盖所有成本，从而在其账单上产生财务损失。在这种情况下，收款人只是试图将此类损失降至最低。总之，根据收款人的目标，存在三个级别的最高折扣：

• 一级：如果收款人希望更早收到付款，甚至获得净收益，则提供折扣；
• 第二级：如果收款人希望更早收到付款但放弃部分加价，则提供折扣；以及
• 三级：如果收款人希望更早收到付款并放弃超过加价的部分，则提供折扣。

与之前对一级折扣的工程经济分析类似，图4(b)从收款人的角度展示了第二级和三级折扣的现金流。这两个级别之间的区别在于收款人希望获得的目标加价率 μ。理性收款人将根据公式(14)进行分析，以比较两种情景下的利润，并确定上限折扣为 $\rho = 1–(1 + \mu)/(1 + M) \cdot (1 + i_{payee})^{l–b}$。该结果表明， $\mu$、$M$、$l$ 和 $i_{payee}$会影响第二级和第三级的最高折扣。公式(15)涵盖了三个级别的最高折扣：对于一级， $\mu$和 $M$ 的取值相等，表示付款人永远不会自愿支付超过所需金额。在这种雄心勃勃且罕见的情况下，收款人希望及时收到相当于货币时间价值的付款，甚至通过节省融资费用获得收益。一级的最高折扣与最低折扣之间通常范围较窄。对于第二级， $\mu$介于零与 $M$ 之间，表示收款人放弃部分原始加价。对于三级， $\mu$介于‐1到零之间，意味着收款人放弃补偿其已经发生的一部分成本。

$$
profit_{take\ discount} \geq profit_{not\ accept\ discount}
\Rightarrow [C \cdot (1− \rho) \cdot (1 + M)− C \cdot (1 + i_{payee})^l] \cdot (1 + i_{payee})^{b − l}
\geq C \cdot (1 + \mu)− C \cdot (1 + i_{payee})^b
\Rightarrow \rho \leq 1− \frac{1 + \mu}{1 + M} \cdot (1 + i_{payee})^{l − b}
$$

（14）

$$
\rho_{ceiling} = 1− \frac{1+ \mu}{1+ M} \cdot (1+ i_{payee})^{l−b}
\quad \text{for} \quad
\begin{cases}
\text{Level 1}: \mu = M \
\text{Level 2}: 0 \leq \mu < M \
\text{Level 3}: -1 \leq \mu < 0
\end{cases}
$$

（15）

如果收款人授予第二级或第三级，则可行折扣范围比第一级更大。在这些级别中，第一级的充分条件（付款人的利率 $i$ 低于收款人的利率 $i$）被放宽。原因是 $\mu$小于$M$，根据公式(15)提高了上限折扣，可能使其远高于折扣下限。在示例5中，假设付款人的利率 $i$ 为7%/月，收款人的利率 $i$ 为5%/月（故意设置为与示例4中所用数值相反的关系），且折扣为 $\rho=10$，30天内付款， $M = 10\%$的成本，第一级 $1 \mu = M$，第二级$\mu = 8\%$（放弃原始加价的20%），以及第三级 $3 \mu =–10\%$（放弃全部原始加价和成本的10%）。有趣的是，根据公式(16)，第一级不存在可行折扣范围；然而，在第二级和第三级分别为{4.4104%, 4.9603%}和{4.4104%, 20.8003%}。这些值将在后续章节中详细说明，并以图形方式展示。已找到数学上可行的折扣范围 $\rho \in {\rho_{floor}; \rho_{ceiling}}$满足目标2。

$$
\text{Level 1} \Rightarrow {1−(1 + i_{payer})^{l−b}; 1−(1 + i_{payee})^{l−b}}
\Rightarrow {4.4104\%; 3.2003\%} = \varnothing
$$

$$
\text{Level 2} \Rightarrow
{1−(1 + i_{payer})^{l−b}; 1− \frac{1 + \mu}{1 + M} (1 + i_{payee})^{l−b}}
\Rightarrow {4.4104\%; 4.9603\%}
$$

$$
\text{Level 3} \Rightarrow
{1−(1 + i_{payer})^{l−b}; 1− \frac{1 + \mu}{1 + M} (1 + i_{payee})^{l−b}}
\Rightarrow {4.4104\%; 20.8003\%}
$$

（16）

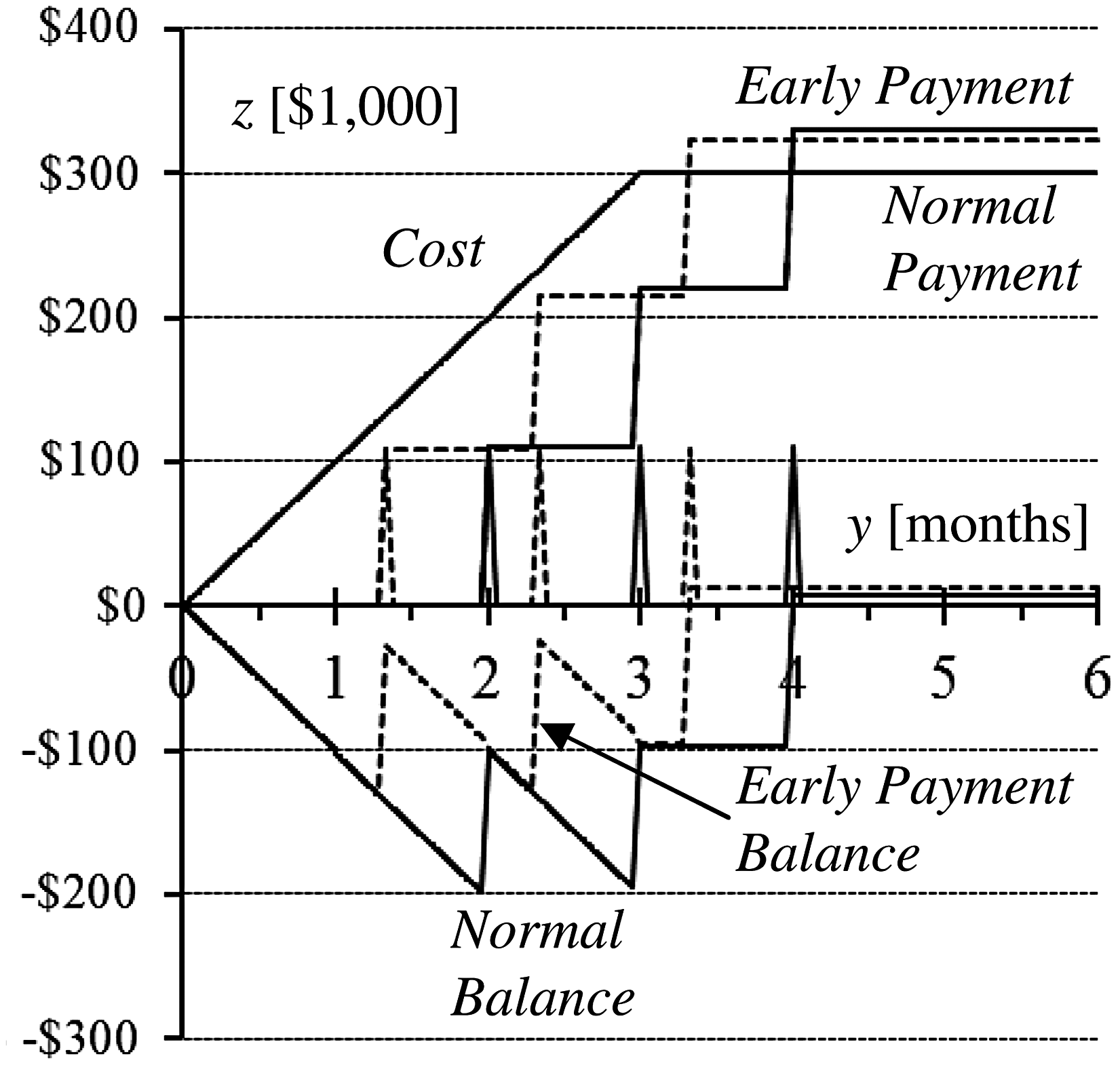
图 6故意夸大了 $M = 200\%$和 $i = 50\%$，以说明三个级别的最高折扣。每一级别显示四个垂直条形：账单、$\rho_1$、 $\rho_2$ 和 $\rho_3$ 。账单条形表示在月末付款，与图4(b)相同。账单用于确定收款人的目标，以校准即时付款折扣，方法如下：在上限折扣处付款，其效果等同于在周期结束时收到付款并具有目标加价$\mu$。所有条形均被垂直分割：左侧显示付款在周期结束时的未来值，右侧减去成本产生的利息，从而得出有效加价$m$。在、低于或高于特定级别中，$\rho_1$为无差异情况， $\rho_2$处于可行范围内，此时折扣会产生净收益，而 $\rho_3$为不可行。向下虚线箭头表示相对于一级目标加价 $\mu_0$基准的实际付款折扣。三级的新基准较低，表明覆盖的成本更少。由于利息在一个期限内复利计算，因此在同一级别内利息相等。

图 6(a)‐账单通过从具有目标加价的正常账单中扣除利息，得到有效加价 $\mu_0 = M$以得出有效加价 $m_0$。图 6(a)-$\rho_1$比较了第 10天付款与第30天付款。前者具有未来值，因为它在20天内具有资金的时间价值；后者产生利息，使总额减少至有效加价 $m_1$，且与 $m_0$相同。图 6(a)-$\rho_2$表明，即使在扣除成本产生的利息后，有效加价 $m_2$仍高于之前的情况，并实现了提前和收益目标。利息节省是条形图中点状区域与斜线阴影区域的差值。然而，如图 6(a)-$\rho_3$所示，提供的折扣若超过上限，则会使 $m_3$小于 $m_0$。第二级的情况与一级类似，但针对的是较小的目标加价 $\mu_0$，提供更优厚的折扣以激励付款方。在三级，有效加价为负值 ，因此不显示加价区域。在扣除利息后，其实际剩余仅能覆盖部分成本。

折扣列线图

可行的折扣 $\rho$受多种因素影响，包括计费到付款延迟 $b$、及时付款期 $l$、付款人’和收款人’的利率 $i$ $i_{payer}$和 $i_{payee}$、原始加价 $M$以及目标加价$\mu$。这些因素中的任何一个都可能改变最终结果。它们之间的关系已在最低折扣和三个级别的最高折扣公式（6）和（15）中定义，这些公式捕捉了可行折扣的本质：可行折扣是收款人愿意提供且付款人愿意接受的折扣，其值介于最低折扣与最高折扣之间，前提是保底低于上限。最低折扣受付款人的财务利率、计费到付款延迟和及时付款期的影响；而最高折扣则根据收款人期望的收款级别，受收款人的财务利率、计费到付款延迟、及时付款期以及原始加价和目标加价的影响。由于三个不同级别会修改相应的最高折扣，因此可通过改变参数值，根据公式（6）和（15）绘制出对应的三张列线图，如图 7–12 所示。

一级（利息带来的净收益))
第二级（损失部分加价))
三级（损失部分成本))

一级列线图

在一级，折扣下限为$\rho_{floor} = 1−(1 + i_{payer})^{l−b}$，最高折扣为$\rho_{ceiling} = 1−(1 + i_{payee})^{l−b}$。可以绘制两种类型的诺模图：一种用于利率‐折扣关系，另一种用于即时付款期‐折扣关系。在图7中，$i$和 $\rho$是变量，而$l$的值保持不变，因此每条曲线代表一个及时付款期情景（例如，$l = 10$天）。这些曲线的曲率由幂函数$z = 1–y^n$引起。它们单调递增，因为其导数为正，例如 $\rho’ = −(l − b) \cdot (1 + i)^{(l − b −1)} > 0$（因为$l < b$）。使用列线图时，首先在横轴上找到付款方利率，然后画一条垂直虚线穿过所需及时付款期的曲线，最后画一条水平虚线与纵轴相交于最低折扣处。重复相同的过程针对最高折扣。这两个值之间的范围表示可行折扣可能取的数值。

在图8中，利率 $i$ 保持不变，而$l$和 $\rho$是变量，因此每条曲线代表一种财务利率情景（例如，利率 $i = 5\%$/每月）。它们的曲率由指数函数$z = 1–a^y$引起。由于其导数为负值，这些曲线单调递减，例如，$\rho’ = −(1 + i)^{(l−b)} < 0$。当利率较小时， $(1 + i)$ 项接近于1，因此在图8中曲率不明显。该列线图使用方法如下：首先找到付款人和收款人对应的利率曲线。然后在横轴上找到所需的及时付款期限编号（例如，$l = 10$）。接着画一条垂直虚线，使其穿过两条利率曲线。再从该垂直虚线与收款人曲线的交点画一条水平虚线，与纵轴相交于最低折扣处。对最高折扣重复相同步骤。这两个值之间的范围即为可行折扣可能取值的区间。

第二级列线图

如果一级的可行折扣范围不存在或过于狭窄，收款人必须转到第二级以寻找次优折扣。在第二级，最低折扣保持不变；只有上限折扣根据公式（15）发生变化。与一级相同，可以绘制两种类型的列线图。在图 9中，最低折扣的曲线束起始于原点，而上限折扣的曲线束则在纵轴上更高的位置起始。这是由于第二级的最低和最高折扣公式不同所致，其中$\rho_{ceiling} = 1−(1 + \mu)/(1 + M) \cdot (1 +利率\ i_{payee})^{l − b}$，因为 $\mu < M$，从而得到幂函数，例如 $z = 1−(1 + \mu)/(1 + M) \cdot y^n > 0$。图 10与图 8类似，但由于第二级的上限折扣不同，上限折扣的曲线相应地上移，从而产生两个重叠的曲线束。

三级列线图

在三级，图11和12的列线图与第二级相似，但由于 $\mu$的范围更宽松，最低和最高折扣曲线之间的差距比之前大得多。与示例5相同， $\mu = –10\%$，表示收款人仅愿意承担90%的成本。

双赢的理论最优折扣

一旦在所需或必要的级别上找到了可行折扣范围，收款人和付款人之间仍然存在通过理论最优折扣实现双赢的空间。理论表明，合同中设定的折扣可能会阻碍进一步优化。另一个障碍是收款人和付款人利率的信息不对称。理论最优是通过使收款人和付款人的趋势相等，并求解未知折扣得到的，如图13所示。通过降低最高折扣（沿收款人曲线的实心箭头），收款人的余额 $zbal_{disc}(y)$ using $i_{payee}$ 上升，直到等于折扣下限，即付款人愿意接受的条件。沿付款人曲线提高折扣将增加付款人的收益，因为付款金额 $zFV_{pay}(y)−zFV_{disc\ pay}(y)$ using $i_{payer}$ 降低。根据公式(6)和(10)，收款人和付款人的各自收益是折扣的线性函数。每个级别的双赢状态用一个圆圈标记，该圆圈在水平方向上位于最低和最高折扣之间；各自的财务收益为各自斜线上水平方向的投影。为了满足图13中一级的条件 $i_{payer} < i_{payee}$，设其分别为 $i_{payer} = 5\%/$month 和 $i_{payee} =7\%/$month。然而，如果假设一个不可行的 $i_{payer} =7\%/$month $>i_{payee} = 5\%/$month，则两条趋势线分离，不存在最优解。但是，如果收款人将上限提升至第二级，则可能实现双赢。在三级时，上限进一步提高，使得实现最优更加容易。通过推导出三个不同级别的列线图，并将理论权衡折扣解释为双赢，从而为实现目标3提供了一个完整的决策过程。

结论与对知识体系的贡献

提前付款折扣为财务经理改善建筑行业的现金流提供了重要机会。这些决策者必须回答几个基本问题，以充分获得潜在收益：所提供的或接受的折扣应有多大？应在什么期限内适用？是否存在一个双方都能受益的区间？参与折扣交易？需要哪些输入值？能否推导出一个通用模型？在哪些情景下，何种折扣水平适合加速付款？为回答这些问题，本文回顾了关于折扣研究的文献，发现Su和Lucko（ 2014）提出的使用奇异函数的综合现金流模型可作为一种准确且高效的工具。

在建筑财务管理与工程经济学领域的知识贡献有三个方面：首先，新模型能够确定由斜向现金流支出和阶梯式现金流入组成的具有变化曲线的正常付款和及时付款情景的余额；该模型考虑了资金的时间价值，并能直接且透明地进行必要计算，从而实现对付款情景的客观比较。其次，可以通过使用已验证模型进行实验，从收款人和付款人的角度探索可行的折扣。当及时付款情景的终值等于（且即将小于）正常付款情景的终值时，由此确定付款人视角下的折扣下限。上限折扣更为复杂，因为它取决于收款人获得付款的紧迫性，即在“更多”与“更早”收到付款这两项相互抵消的目标之间权衡其相对重要性。针对收款人定义了三个级别的最高折扣，分别对应于因折扣而产生的利息净收益、部分利润加价的损失或部分成本的损失，按严重程度由低到高排序。这些结果已通过基于新型现金流模型的工程经济分析得到验证。第三，已推导出两种类型的列线图，分别描述了利息–折扣和及时付款期–折扣之间的关系。这些列线图是通过在包含折扣率 $\rho$、利率 $i$ 和及时付款期 $l$ 的折扣方程中保持一个值不变，同时改变另外两个值得到的。这些列线图涵盖了本文提出的关于及时付款折扣的新理论中的计算。财务决策者可以轻松使用它们通过图形确定其特定情景下的可行折扣，而无需单独评估底层的数学方程，除非需要更精确的折扣值。它们为建设项目中的折扣决策过程提供了简便的支持。尽管可以准确确定双方都认为是双赢的理论最优值，但需承认在实际应用中，即时付款折扣可能会为了便于使用而取整，例如四舍五入到最接近的1%的四分之一。即便如此，它仍然是及时付款的激励。

预计该即时付款折扣理论可转化为其逆向形式，以应对延迟付款的罚金问题。尽管此类财务费用可通过计算逾期债务的利息简单得出，但收款人可能希望设定特定期限，在这些期限内收取固定等级的罚金；或者收款人可能同意部分债务豁免，以至少获得部分付款，即使付款延迟。这同样是一种折扣情景，只是付款期限被延长。这些问题将在未来研究中加以探讨。

总之，传统的2/10，净30方式虽然广为人知，但存在诸多缺陷。它仅代表了折扣及其期限可能解决方案谱系中的一 个单一节点，因而排除了对一系列折扣方案的探索。此外，该方法未考虑双方的融资利率，而这些因素显然是本分析中至关重要的输入条件。再者，它忽略了收款人特定情境下的目标，而收款人的紧迫性决定了其愿意提供的折扣水平。最后，该方法掩盖了一个核心洞察：即如果实现及时付款，如果折扣设置得当，其双赢情景可使收款人和付款人都受益。因此，本文基于采用奇异函数扩展的现金流模型，建立了一个关于即时付款折扣的理性财务决策理论模型。