参数控制多涡卷混沌系统

一种新型的参数控制多涡卷混沌吸引子及其电路设计

1 引言

混沌系统的研究因其在流体流动网络到电路设计等领域的广泛应用而受到广泛关注[1]。在这些混沌系统中，具有多卷吸引子的系统尤为重要，因为它们可应用于许多工程应用[2–11]。在过去二十年中，人们进行了大量研究工作，致力于多卷吸引子[2–6]及其在安全通信、电路设计、FPGA实现、信息处理和加密中的应用[7–11]。Chua和Komuro提出了一个双涡卷吸引子[12]。马丹[13]对蔡氏电路的性质与改进进行了全面分析，从而通过简单电路实现了产生各种复杂多涡卷混沌吸引子的新构型。苏延斯和范德瓦勒[14]提出了一类仅用一组数学函数生成的多卷吸引子。

需要注意的是，多卷吸引子通常通过向耗散系统中引入多个平衡点来获得，使得每个固定点周围都会产生涡卷。然而，也存在一些已知的多卷吸引子并非由不稳定平衡点的不稳定流形形成[13,15,16]。它们通常属于具有隐藏吸引子的系统类别[17–21]。

巴拉哈斯‐拉米雷斯 [16]提出了一种简单的设计策略，可实现具有理想平衡点位置的多卷吸引子，并揭示了全局动力学中预期的过渡行为。除了分段线性函数 [22,23],外，还有一些研究致力于饱和 [24],三角函数、绝对值、多项式、双曲函数 [25],调制、符号以及非线性滞回函数 [26]。陆和陈 [27]研究了生成多卷吸引子的不同设计方法，并讨论了其潜在应用。

所有这些研究工作揭示了函数依赖的多涡卷系统，正如预期的那样，需要单独的函数来生成多个涡卷，这促使我们提出以下关键问题：1）为什么多卷吸引子必须是函数依赖的？2）为什么不能是参数依赖的？受这些问题的灵感启发，我们对蔡氏电路进行了改进，并且据我们所知，首次提出了参数控制的多卷吸引子。

2 参数控制的多涡卷混沌吸引子（PCMCA）

经典蔡氏系统[12]由以下状态方程描述：

$$
\dot{x}= \alpha(y - x - f(x)), \quad \dot{y}= x - y+ z, \quad \dot{z}= -\beta y, \tag{1}
$$

其中非线性函数 $ f(x) $ 定义为

$$
f(x)=
\begin{cases}
bx+ a- b & \text{for } x \ge 1 \
ax & \text{for } -1 \le x \le 1 \
bx - a+ b & \text{for } x \le -1
\end{cases} \tag{2}
$$

该系统可生成隐藏的单涡卷和双涡卷吸引子。蔡氏电路产生双涡卷吸引子 [28, 29], 当 $\alpha= 9$, $\beta= 100/7$, $a= -1.14$, $b= -0.7$ 时，例如。本文通过替换蔡氏系统（1）中的分段线性函数（如式(3)所示），并引入控制参数 $c$ 通过式(1)中的 $x$ 状态，构造出一个多卷吸引子。所提出的系统如式(4)所示。

$$
f(x)= \mathrm{sgn}(x)+ \mathrm{sgn}(x+ b)+ \mathrm{sgn}(x - b)+ \mathrm{sgn}(x+ 2b)+ \mathrm{sgn}(x -2b), \tag{3}
$$

$$
\dot{x}= g(y - ax+ f(x))− c, \quad \dot{y}= x − y+ z, \quad \dot{z}= −dy. \tag{4}
$$

许多研究致力于通过修改蔡氏电路[30–32],来构造多卷吸引子，但均采用了多个分段线性函数[7,27,33–38]。我们所提出的多涡卷系统的新颖性在于，涡卷数量由参数控制，而非通过改变分段线性函数实现。相较于其他具有至少五个涡卷的多涡卷系统，所提出的系统在项数上预期更为简单；生成我们的多卷吸引子仅需一个函数。因此，我们基于[39]中描述的准则之一提出了一种新的混沌系统。

表1. 多涡卷生成函数。

序号	多涡卷生成的函数类型	参考文献
1	分段线性函数	[22,23]
2	饱和函数	[24]
3	三角函数	[25]
4	多项式函数	[25]
5	双曲函数	[25]
6	滞回函数	[26]
7	符号函数	[51]
8	锯齿函数	[30]
9	具有可变参数的固定函数	本文

本文提出的多卷吸引子与表1中的一些函数依赖多卷吸引子进行了比较。

表2. 系统(4)的不同情况。

多卷吸引子	a	b	g	d	c	图
双卷	0.3	7	9	15	2.5	1a
三卷	0.3	7	9	15	1.5	1b
四卷	0.3	7	9	15	1	1c
五卷	0.3	7	10	12.5	0.4	1d
六卷	0.3	7	10	12	0	1e

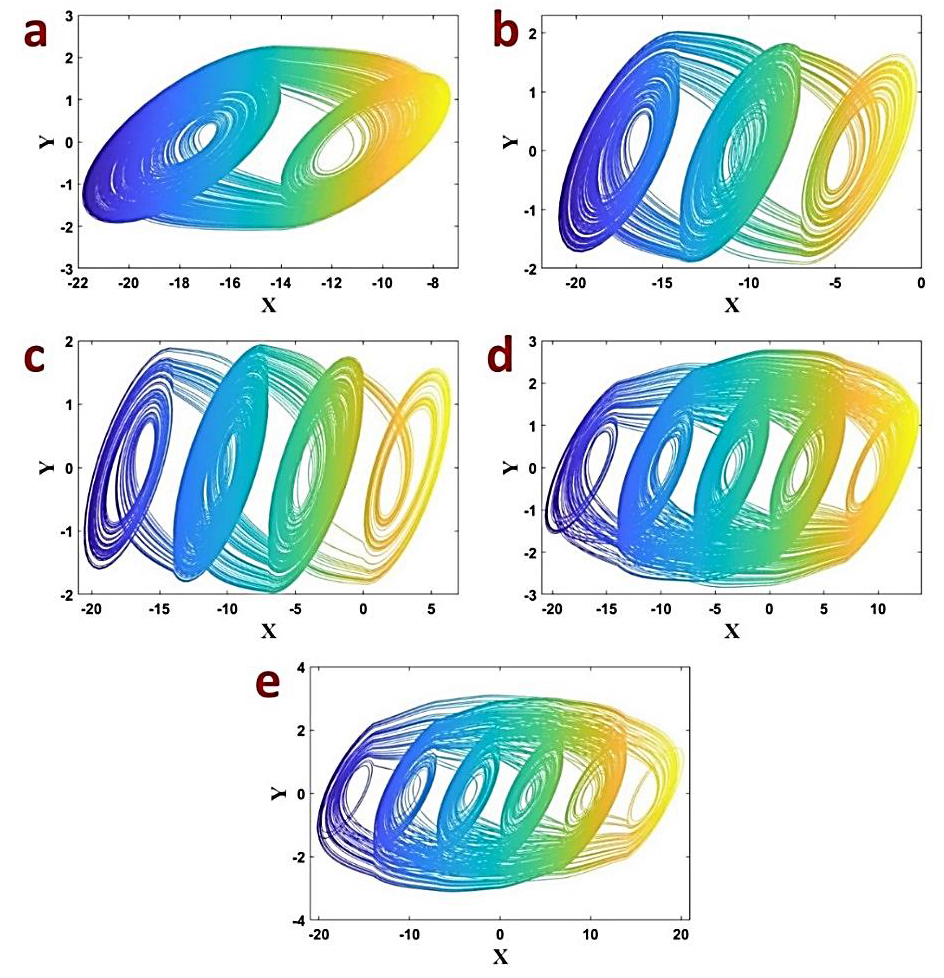
3 PCMCA的动力学特性

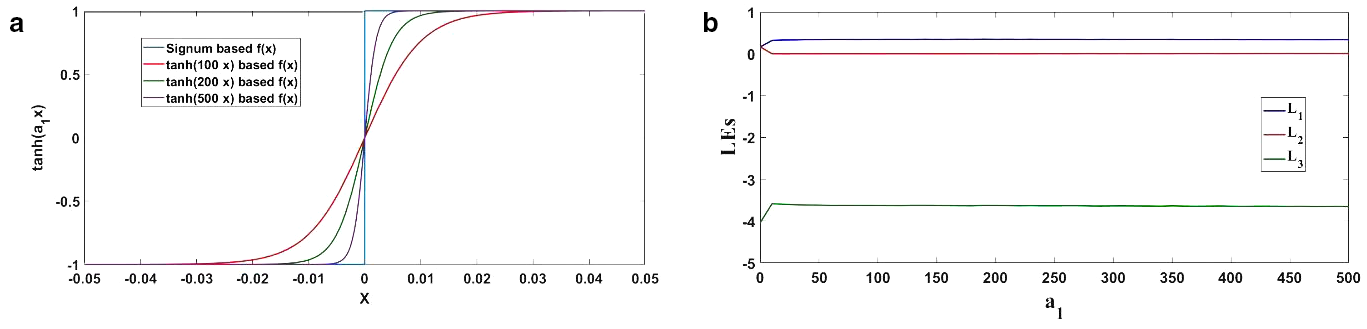
使用沃尔夫算法对PCMCA的有限时间李雅普诺夫指数（LEs）进行了计算，积分时间为100000秒，并采用给定的初始条件[0.1, 0, 0.1]。在计算李雅普诺夫指数时需特别注意数值计算的准确性，因为不当使用常规方法可能会引发一些问题[41–44]。为了计算LEs，用$\tanh(a_1 x)$替代符号函数以避免可能出现的数值奇点。使用较大的 $a_1$ 值能够更精确地逼近符号函数，如图2(a)所示，但这可能为模拟和数字电路中的实时实现带来复杂的困难。因此，我们在LEs的计算中选择 $a_1 = 100$，而使用 $a_1 = 100$ 和 $a_1 = 500$ 时仅观察到可忽略的差异(< 0.0006)。图2(b)展示了该系统在不同 $a_1$ 值下的有限时间局部李雅普诺夫指数。多涡卷系统的LEs及其对应的Kaplan‐Yorke维数($D_{KY}$)列于表3中。

表3. PCMCA系统的有限时间局部李雅普诺夫指数。

多卷吸引子	LEs	$D_{KY}$
双卷	0.347, 0, −3.625	2.095
三卷	0.347, 0, −3.623	2.095
四卷	0.348, 0, −3.599	2.096
五卷	0.726, 0, −3.584	2.2
六卷	0.754, 0, −3.466	2.217

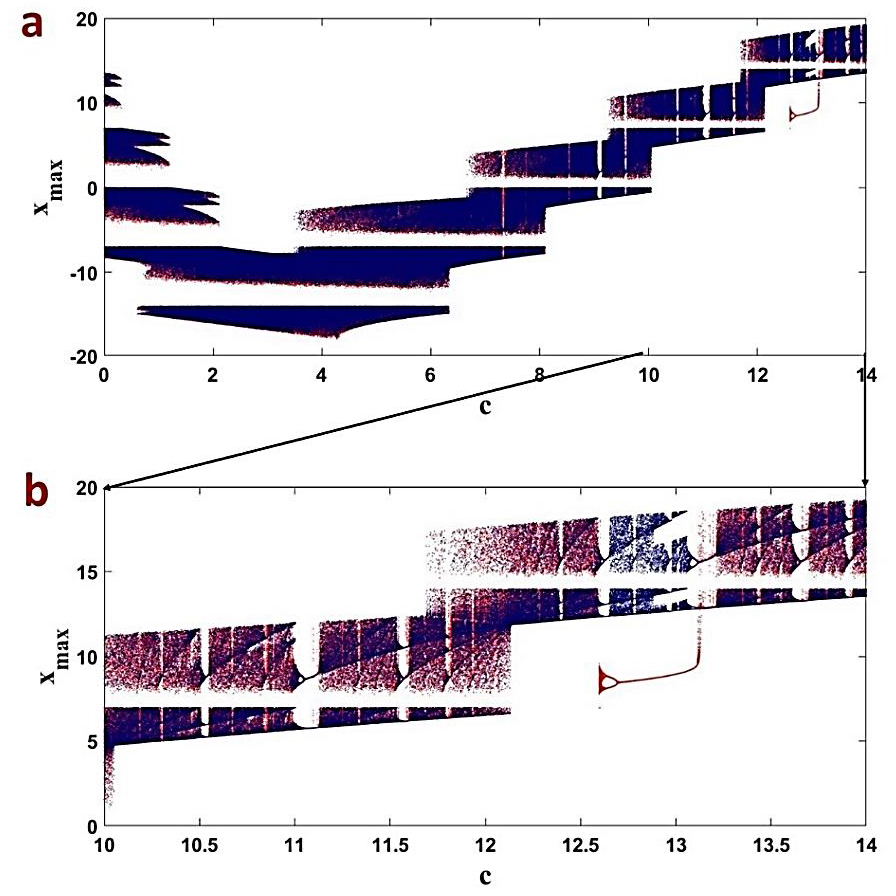
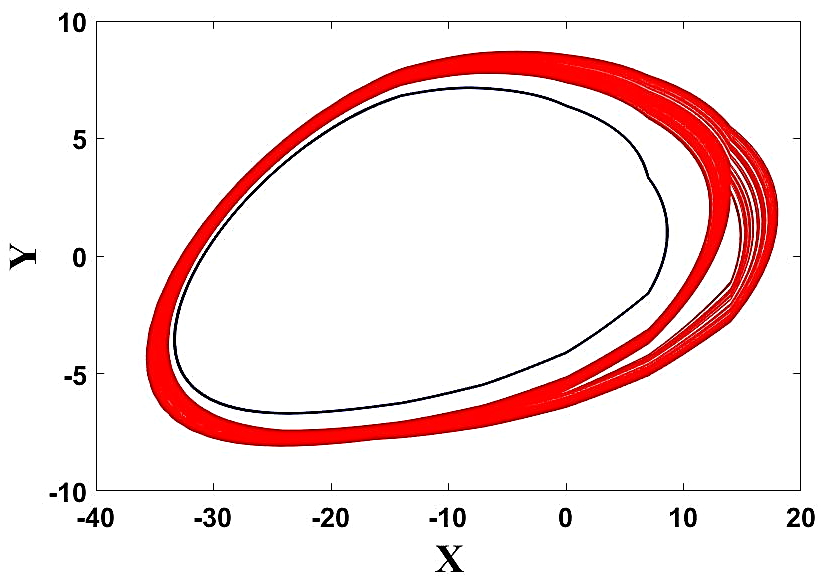
PCMCA系统的动态行为通过绘制其分岔图与 $c$ 的关系来可视化，其中 $c$ 作为控制参数，并使用表3中列出的其他参数，针对双涡卷系统。图3显示了PCMCA系统的分岔图。蓝色点表示通过正向延拓（在每次迭代中将控制参数递增，并将初始条件重新设置为状态变量的终值）得到的分岔，而红色点表示通过反向延拓（在每次迭代中将控制参数递减，并将初始条件重新设置为状态变量的终值）捕获的分岔。注意我们绘制了状态变量 $x$ 的局部最大值。图3(a)展示了控制参数在 $0< c<14$ 范围内的分岔图 vs. $c$。图3(b)显示了在 $12.6< c< 13.2$ 范围内的分岔图，揭示了极限环与混沌吸引子在 $12.6< c<13.2$ 范围内的共存现象。此外，值得注意的是，在初始条件分别为[−18, 5, 34]和[−0.1, 0, 0.1]，且 $c= 12.83$ 的情况下，观察到了单卷混沌吸引子（红色）与周期‐1极限环（蓝色）的共存，如图4所示。需要注意的是，这种多稳态特性使得所提出的系统更具应用吸引力，因为具有共存吸引子的多稳态系统在非线性动力学中具有重要意义[45–50]。

4 电子电路四涡卷PCMCA系统在工程应用中的电路设计

我们在此基于运算放大器（OP‐AMP）器件设计了四卷参数控制多涡卷混沌吸引子（PCMCA）的电子电路，以用于广泛的工程应用。我们利用OrCAD PSpice程序进行电子电路的设计。需要注意的是，尽管PsPice软件基于实际电路元件，但仍存在离散化问题，其使用可能导致错误结论，特别是对于隐藏吸引子[21]。四涡卷PCMCA系统状态变量 $x$ 和 $z$ 的取值范围为−25V至30V。注意，电路中所用运算放大器器件的最大供电电压为 ±18Vdc。因此，状态变量 $x$ 和 $z$ 的取值及初始条件按5倍缩放，如公式(5)所示。同时，系统及分段线性函数($f$)经5倍缩放后的表达式见公式 (6)。我们将缩放后系统的状态变量重新命名为 $X$、 $Y$ 和 $Z$。缩放后系统的初始条件为 $X_0= 0.02$、 $Y_0= 0.02$ 和 $Z_0= 0.02$。

$$
X= \frac{x}{5} \Rightarrow \dot{X}= \frac{\dot{x}}{5}, \quad
Z= \frac{z}{5} \Rightarrow \dot{Z}= \frac{\dot{z}}{5}, \tag{5}
$$

$$
\dot{X}= -1.8Y+ 2.7X -1.8f+ 0.2, \quad \dot{Y}= -5X+ Y -5Z, \quad \dot{Z}= 3Y, \tag{6}
$$
where
$$
f= \mathrm{sgn}(x)+ \mathrm{sgn}(x+ 1.4)+ \mathrm{sgn}(x -1.4)+ \mathrm{sgn}(x+ 2.8)+ \mathrm{sgn}(x -2.8).
$$

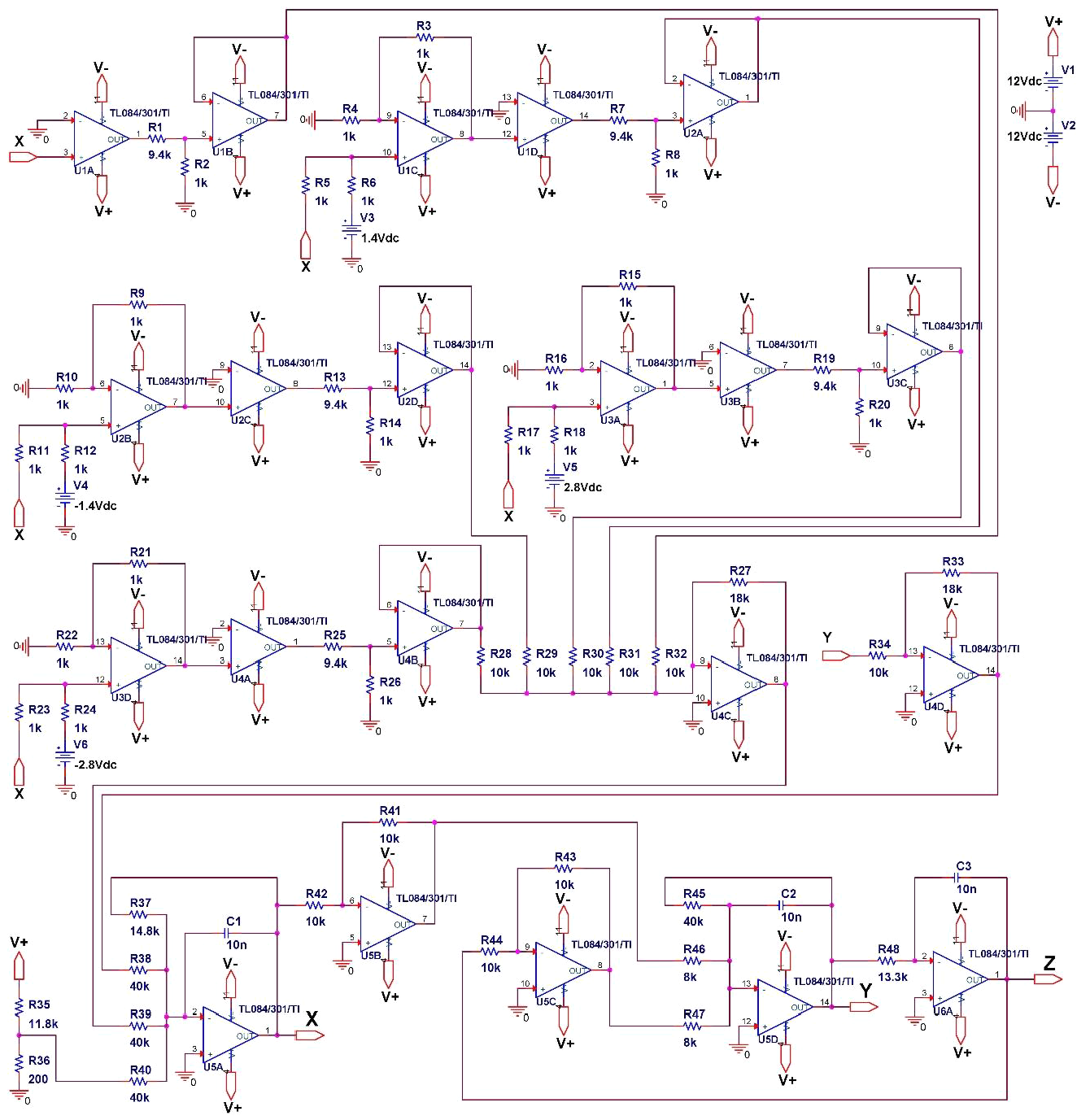
表4. 电路中电子元件的取值。

器件名称	取值
U1, U2, U3, U4, U5, U6	TL084 集成电路
C1, C2, C3	10 纳法
R1, R7, R13, R19, R25	9.4 kΩ
R2, R3, R4, R5, R6, R8, R9, R10, R11, R12, R14, R15, R16, R17, R18, R20, R21, R22, R23, R24, R26	1 kΩ
R27, R33	18 kΩ
R28, R29, R30, R31, R32, R34, R41, R42, R43, R44	10 kΩ
R35	11.8 kΩ
R36	200 Ω
R37	14.8 kΩ
R38, R39, R40, R45	40 kΩ
R46, R47	8 kΩ
R48	13.3 kΩ

电子电路的状态空间方程为

$$
\dot{X}= -\frac{1.8}{R_{38} C_1} Y + \frac{1}{R_{37} C_1} X - \frac{1.8}{R_{39} C_1} f + \frac{0.2}{R_{40} C_1},
$$
$$
\dot{Y}= -\frac{1}{R_{46} C_2} X + \frac{1}{R_{45} C_2} Y - \frac{1}{R_{47} C_2} Z,
$$
$$
\dot{Z}= \frac{1}{R_{48} C_3} Y. \tag{7}
$$

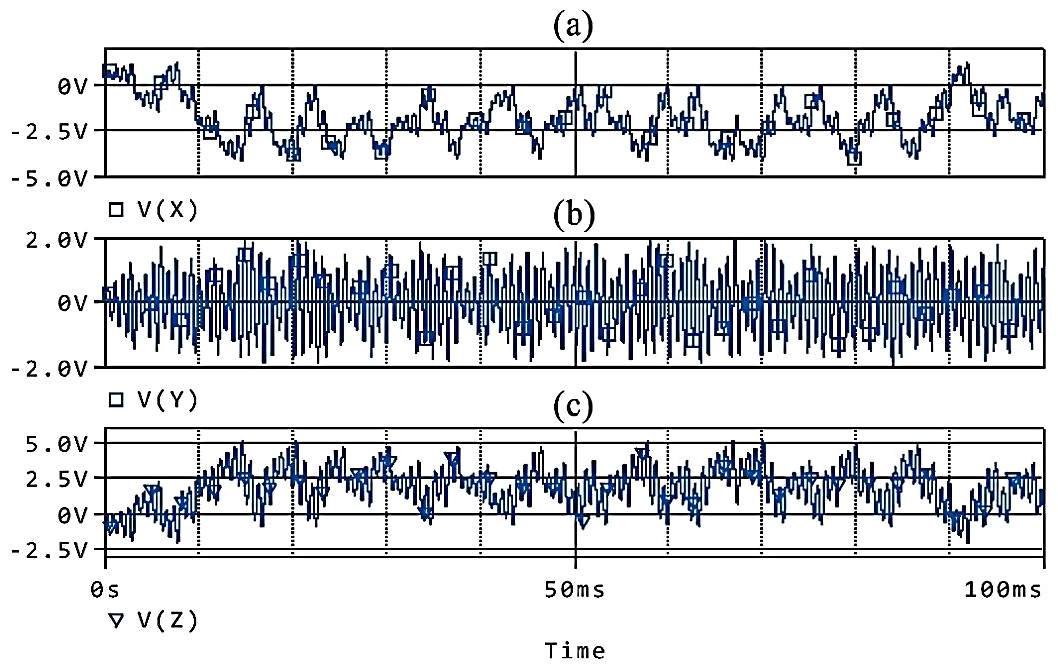
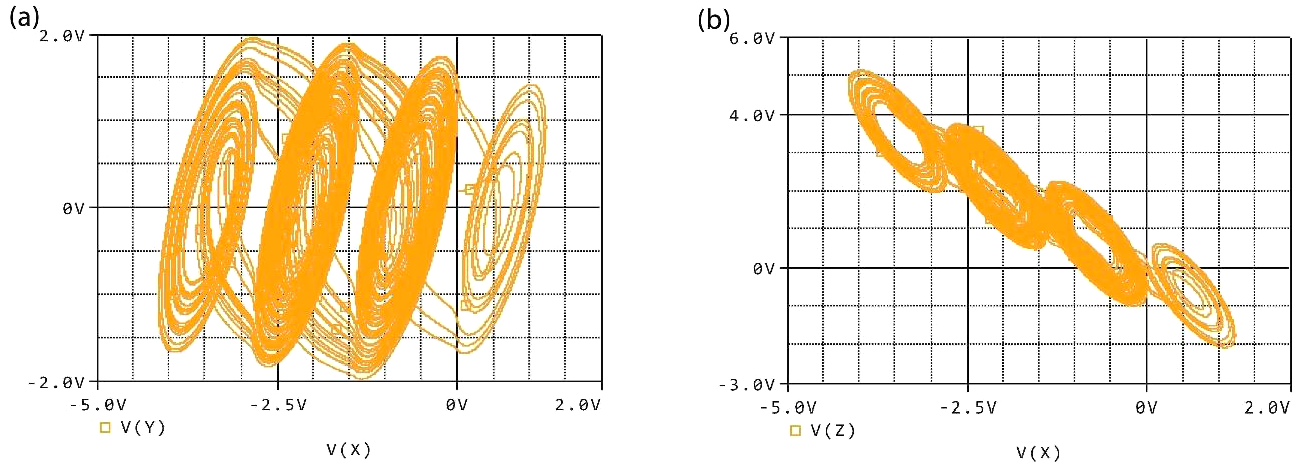
图6显示了为缩放后的四涡卷PCMCA系统（6）设计的电子电路的状态变量（$X, Y, Z$）。状态变量的变化范围为 $-5V < X < 3V$、 $-2V < Y < 2V$ 以及 $-3V < Z < 6V$。因此，可以明确得出结论：缩放后的系统（6）在电子电路领域具有实际应用性。图7展示了电子电路的相图。值得一提的是，四涡卷PCMCA系统（图1(c)）的相图与所设计的电子电路的相图（图7(a)）相同。随后，我们可以很容易地得出结论：基于所设计的电子电路，PCMCA系统适用于广泛的工程问题。

5 结论

本文提出了一种新型的多涡卷混沌系统，其涡卷通过参数控制而非函数依赖实现。该系统设计的显著优势体现在其在硬件中的实时实现上，而单一函数的实现通常需要更少的资源。此外，仅通过改变参数即可控制涡卷，此处通过调节分立元件来实现。所提出的系统展现出丰富的动力学行为，我们利用有限时间局部李雅普诺夫指数和分岔图等强大工具对其进行了深入研究。我们捕捉到了极限环与混沌吸引子的共存现象，以及在某些初始条件和关键控制参数 $c$ 取值下，单卷混沌吸引子与周期‐1极限环的共存现象。这揭示了所提出系统的多稳态特性，这一特性被认为是广泛非线性动力系统中极为重要的性质。最后，我们使用现成组件将所提出的系统实现了电子电路，并给出了仿真结果以评估这种新颖的电路设计。这类多涡卷混沌系统，仅需在模拟电路中简单改变电阻或电容值便可产生不同的涡卷，在基于混沌的通信系统中具有很高的应用价值。