光纤扫描器机电模型设计

用于内窥镜的光纤扫描器机电模型设计与测试

1 引言

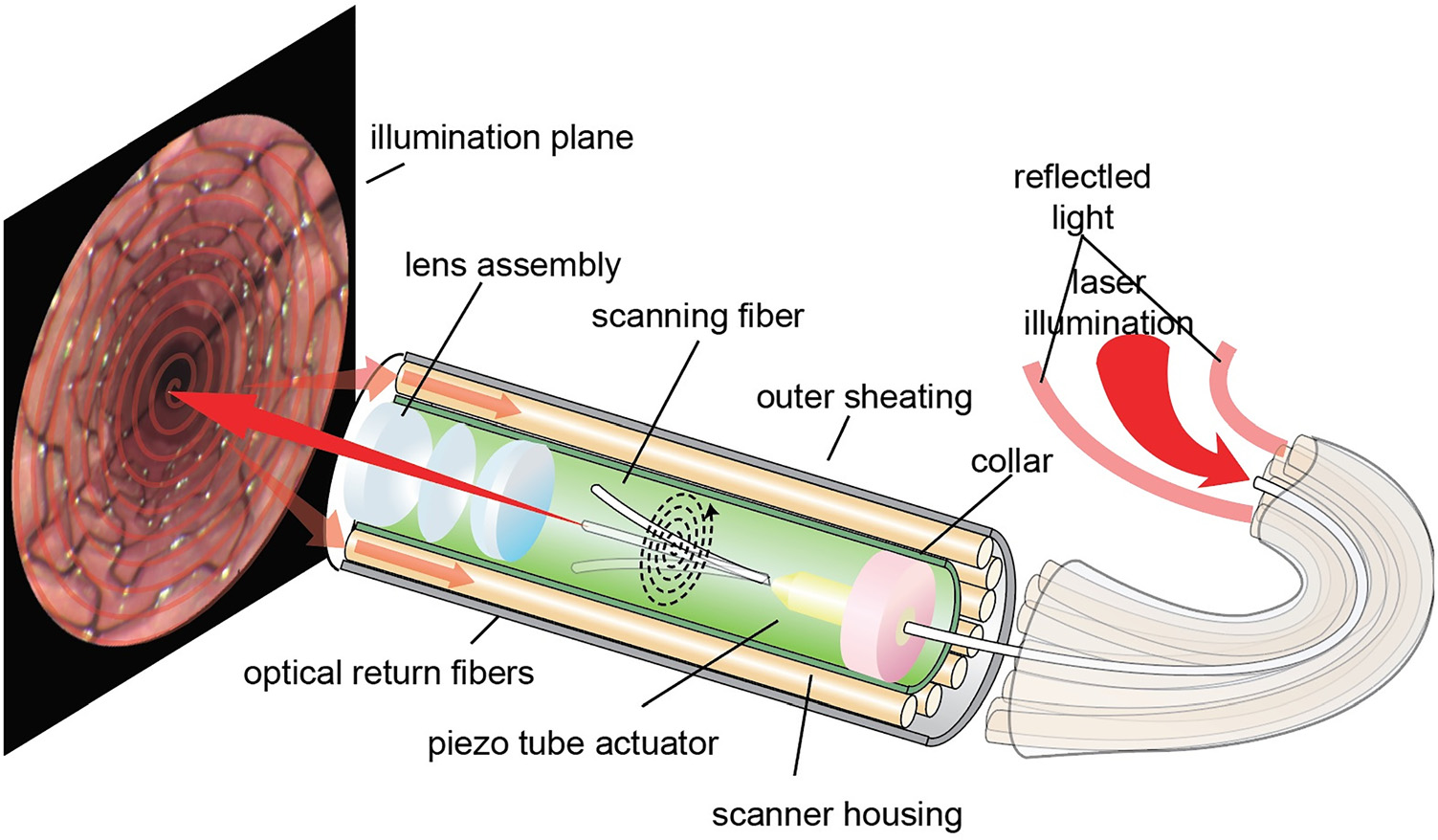
超细内窥镜和导管内窥镜正在被开发用于提供高质量的心血管系统可视化，以实现对易损斑块的激光诊断[1]以及支架置入等介入装置的应用[2]。这些新工具帮助介入心脏病学家对抗在美国仍为#1 killer in the U.S.的心血管疾病[3]。用于提供前视视频的谐振或近谐振光电机械光纤扫描仪非常适合小型化至关重要的应用场合，例如细长柔性内窥镜[2,4]。这些扫描器的根本优势在于，能够使用具有每个显示像素至少一个传感器元件的视频传感器芯片，获取比传统相机更多像素的视频。例如，一种最紧凑的双轴光学扫描仪采用振动单模光纤，可制成1毫米直径前视导管内窥镜，并具有广泛的应用前景[4]。这种扫描光纤内窥镜（SFE）采用基底激励光纤悬臂梁作为光电机械扫描器，通过压电管驱动，其功能示意图如图1所示。在过去十年中，SFE已被应用于广泛的医学成像领域，例如腔内癌症的筛查[4],以及最近在人体动脉中进行基于激光的荧光成像和心血管疾病诊断[5]。

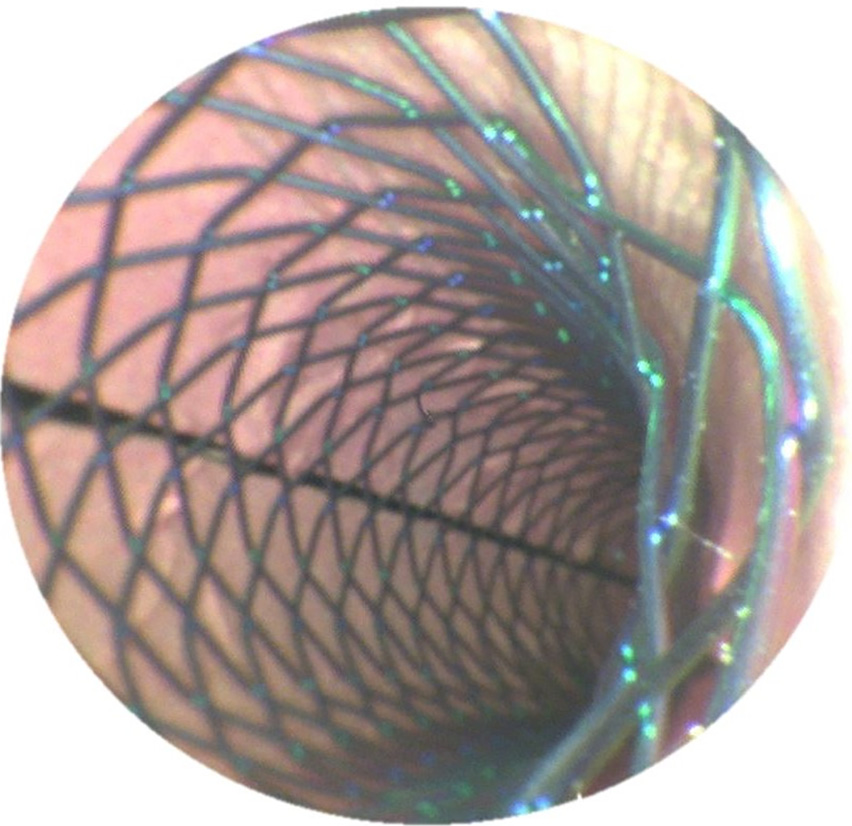
扫描光纤内窥镜的图像质量是光源、扫描器动态特性、透镜系统和探测器电子器件的函数。由于激光诊断具有优势（例如，早期癌症的荧光分子探针成像），光源为一个或多个激光器，通过光纤将光输送至人体内部能够保持单模强度分布的光纤。光纤扫描器的偏转幅度决定了光学系统设计所能实现的最大视场（FOV）和横向空间分辨率。此外，光学扫描器的共振频率决定了其在光探测器和采样电子器件的限制范围内实现最大帧率的能力。因此，光电机械装置的设计是这些超细内窥镜实现最高性能的关键组件。对于SFE而言，设计目标是在保持高质量视频成像的同时，最大化用于管腔壁成像的视场（FOV），以满足疾病诊断和支架检查等应用需求（图2）。最优SFE探头设计的理想视场（FOV）为 80度。图像分辨率的目标通常是在给定光学元件成本、尺寸以及采样率限制的前提下，尽可能最大化分辨率。一种直接增大视场的方法是增加光纤尖端振动的偏转幅度。然而，若扫描区域增大而振动频率未相应提高，则每帧图像的扫描线数将减少，从而导致分辨率降低，这一点在镜面扫描器中也同样适用[6]。因此，为了保持SFE的高分辨率，通过增大光纤尖端偏转来扩大视场的同时，必须伴随提高扫描器的一阶共振频率。

由于各系统参数之间的相互关系，设计SFE探头中的扫描光纤系统并非易事。SFE是一种机电一体化产品，它由多个协同工作的子系统合成，涉及通过软件中实现的复杂控制架构[7,8]所控制的机械和电气部件。因此，SFE的开发面临着许多与机电一体化产品的开发[9]常见的挑战。这些挑战包括对多个耦合系统的建模与控制，以及利益相关者之间缺乏共同语言等问题。在讨论问题和想法时涉及不同学科，以及在多个学科之间同步组织并行工程和设计工作的困难[9,10]。一个具有足够保真度的模型，能够整合各种系统参数并准确预测设计的动态特性，将大大加速该技术的发展。基于模型的设计将允许在无需实际构建的情况下评估SFE设计，从而节省时间和成本。为了改进这些制造工艺并生产高性能、可靠的成像系统，还需要充分理解设计要求对制造过程中各个步骤的敏感性。

对这些系统动力学的先前建模工作可分为以下几类。其中一类是仅使用线性[11,12]或非线性[13]梁理论来建模悬臂式光纤。实际系统的输入是施加在压电管上的电压。但在上述两类方法中，系统的输入被设定为光纤的基座位移，并假设该位移保持恒定，即使几何形状和质量发生变化也是如此。第二种方法是通过在扫描器的实验数据上拟合集中质量模型，并采用系统辨识技术[7]，估计一个降阶传递函数。该方法的精度依赖于数据采集装置。但更重要的是，该方法首先需要构建扫描器，在设计扫描器几何结构时无法预测系统几何变化所引起动力学特性的改变。此外，也有研究针对压电致动器与扫描光纤之间的整体机电相互作用进行建模[14]。该研究对象是由四个独立的压电致动器构成的方形管。该研究探讨了驱动电压以及扫描光纤和方形管长度变化时系统动力学的改变。模型在预测均匀光纤悬臂系统的共振频率方面与实验结果表现出良好的一致性。

本文的主要研究重点是探讨光纤悬臂的非均匀几何设计如何影响整个SFE系统的动力学特性，从而有助于提升SFE在先进医疗应用中的几何和光学设计。第一步是建立基于高保真有限元（FE）的扫描光纤模型。该系统包含压电管的机电动力学与振动光纤的机械动力学之间的耦合。在完成实验验证后，第二步是利用该有限元模型设计适用于SFE探头的特定透镜组件，尽管这部分内容不在本文讨论范围内。为了实现第一步，所采用的光机有限元模型基于几何结构，非常适合用于光纤扫描仪的基于模型的优化设计目标。这一先进模型无需假设光纤基底偏转为恒定值，克服了以往部分模型的局限性。这是首个针对先进光纤扫描仪的完整模型，例如为超细内窥镜最大化扫描频率和振幅而设计的非均匀蚀刻玻璃悬臂结构。

针对在提高共振频率的同时增大光纤尖端位移这一具体设计目标，利用模型对微加工光纤悬臂的不同设计进行评估。

特别是，理论上和实验上评估了改变光纤悬臂长度及其沿长度方向直径的影响。基于这些结果，构建并测试了光纤扫描器设计，以验证预测的光纤尖端偏转和共振频率的提高。最后，采用一种新的微加工工艺精确修改悬臂式玻璃纤维的物理尺寸，并极其仔细地测量这些尺寸，以便将实验结果与光纤扫描器的新耦合模型进行直接比较。

2 机电耦合模型

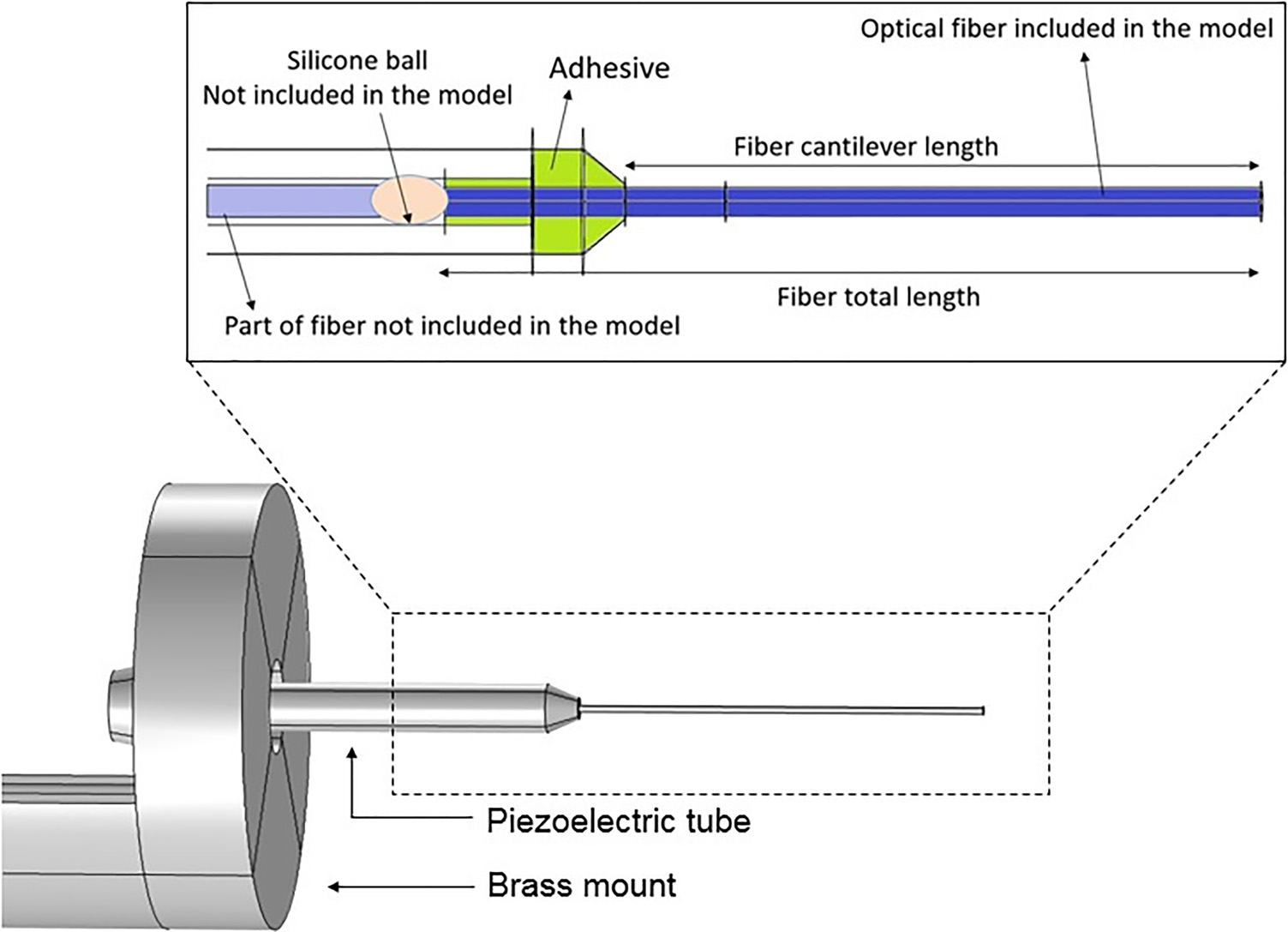
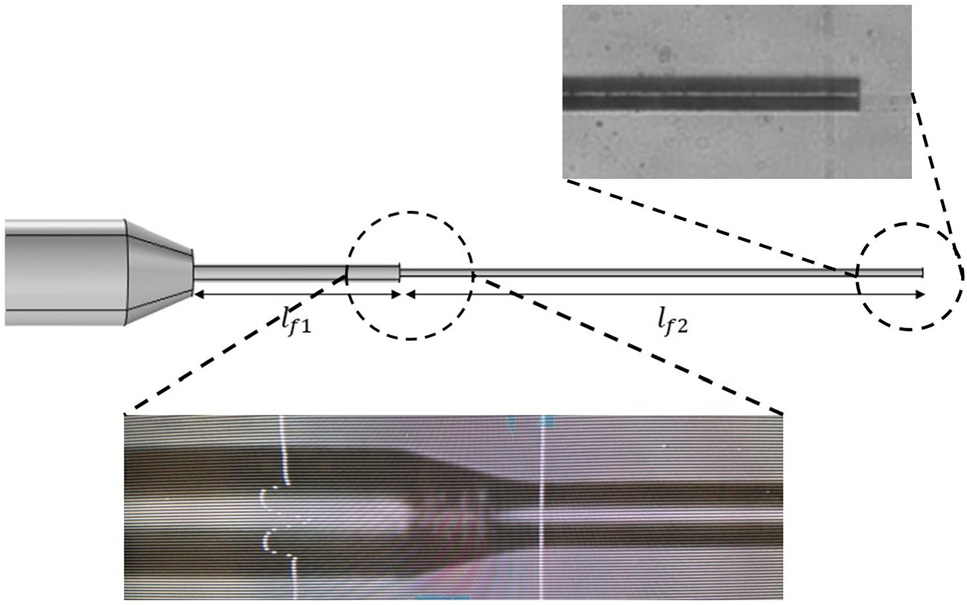
扫描器由一根位于压电管内的光纤组成，如图3所示。该压电管由PZT‐5A材料制成（日本万能町永峰制造有限公司），表面带有金属涂层，作为电极使用。通过粘合剂将光纤连接在压电管的远端悬臂端。同时使用硅胶球将光纤固定在压电管内部。在压电管的悬臂端外部，一段光纤被暴露出来形成悬臂结构。需要注意的是，金属涂层和硅胶球未包含在模型中。施加在压电管上的正弦波形式的电信号驱动会使压电管发生弯曲，从而导致光纤悬臂的基部产生位移。如果驱动频率接近光纤的一阶共振频率，则光纤尖端会产生大幅偏转，并以此驱动其按螺旋模式进行光学成像。这种工作方式使系统成为一种近共振光电机械扫描仪。

准确建模光纤扫描器系统的简单方法是仅使用欧拉‐伯努利梁理论将光纤建模为基底激励悬臂，然而这是一种非耦合模型，其中仅包含悬臂光纤的动力学特性。本文探讨的方法是基于三维有限元的压电管和光纤的模型，其中压电管被建模为根据压电性线性方程（公式（1）和（2）[15]）行为的域，而光纤则被建模为由弹性方程（公式（3）[16]）控制的线弹性材料

$$
r = Ce - e^T E \tag{1}
$$
$$
D = e\varepsilon + \varepsilon_s E + D_r \tag{2}
$$
$$
r = Ce \tag{3}
$$

这里，r、e和C分别为应力、弹性应变和弹性张量，E表示电场，D和Dr分别表示总电位移和由剩余极化引起的电位移。此外，e表示耦合矩阵，该参数用于描述压电材料中力学效应与电学效应之间的耦合关系，即应力与电场之间以及电位移与应变之间的耦合。最后，es是材料介电常数。两个区域通过第三个区域耦合在一起，该区域被建模为具有粘合剂估算属性的不同线性弹性材料，如图3所示。压电管区域的材料坐标系方向设置为极化方向沿径向。通过对轴向截面使用三角形单元进行网格划分，然后围绕纵向轴扫掠该截面，生成对称网格。该扫描器通过粘合剂固定在黄铜支架上，二者均被建模为线性弹性材料区域。在支架的近端施加固定边界条件，并在压电管顶部和底部的电极上施加电势边界条件。

有限元模型在 COMSOL MULTIPHYSICS（版本5.2）中求解，使用特征值求解器获得共振频率，并使用频域求解器获得光纤尖端偏转的频率响应。在 COMSOL中估算动态系统阻尼时所需的一个参数是品质因数，其定义为共振频率与共振峰 -3dB带宽的比值。为了对系统的不同组件赋予适当的阻尼量，压电管、扫描光纤和粘接接头分别采用不同的品质因数。压电管的品质因数由制造商提供。假设光纤的内阻尼相比压电管更低；因此，其品质因数比压电管的品质因数高两个数量级。剩余的阻尼来自粘接接头，粘接接头的品质因数通过实验数据进行调节。对锥形扫描光纤探针的研究还表明，尽管光纤尖端在空气中的速度存在，主要的阻尼机制仍是内阻尼[17]。因此，本研究未考虑空气阻尼。

实际上，施加到光纤悬臂上的基座位移量取决于光纤悬臂本身。例如，如果光纤体积较小，因而总质量较低，则压电管所承受的惯性负载较小，从而使光纤能够产生更大的偏转。需要注意的是，对于5 kHz共振扫描器，悬臂式光纤的质量通常约为压电管质量的12%。因此，压电管上的负载不可忽略。在以往的解耦模型[11–13],中，压电管被简化为假设具有恒定的基座位移。本文提出的耦合模型则不需要这一假设。由于耦合机电模型的输入是电驱动信号，这种负载的变化将在模型输出中得到体现。

为了便于接触光纤以修改光纤几何形状，SFE外壳（如图 1所示）被替换为黄铜支架（如图3所示）。因此，尽管本研究中使用的计算机辅助设计模型与来自类似装置的实验数据进行比较，但实际的SFE在压电管底部会具有质量更小的外壳。此外，光纤扫描器的共振频率取决于光纤振动所处的介质[参考文献 [17]]。由于未对光纤周围的空气进行建模，该模型估算的共振频率适用于真空中的系统，这会比在空气中工作的相同系统略高。此前也已发现，某些SFE结构可能表现出非线性共振行为[12,13]。由于该模型基于线弹性材料模型（公式 (3)）以及压电材料的线性本构方程（公式(1)和 (2)），因此无法模拟此类非线性动力学行为。

3 实验设计

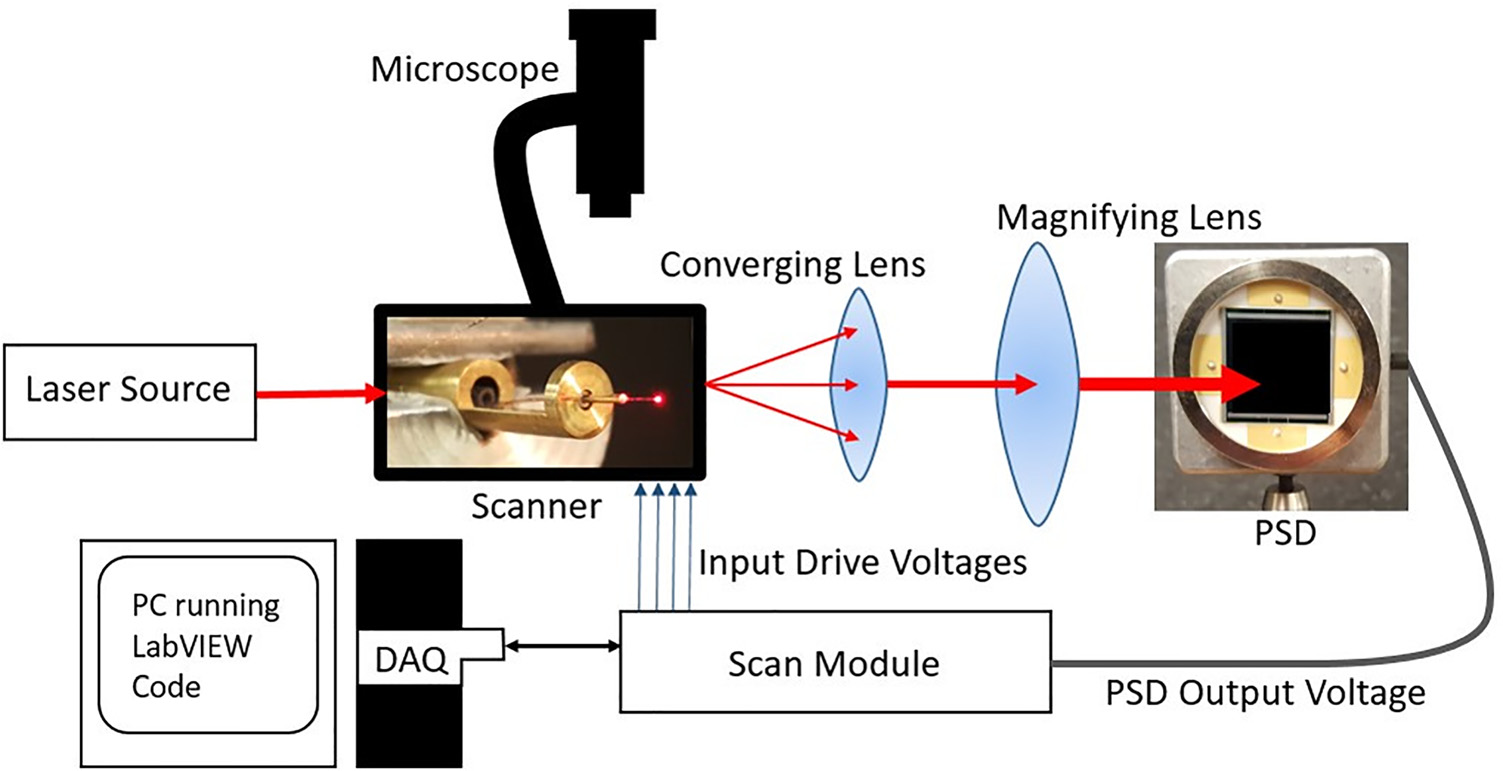
实验装置由安装在黄铜支架上的扫描器组成，该支架固定在显微镜的载物台上，如图4所示。光纤的另一端连接到激光源，通过光纤振动端输出的光经过透镜组件准直后，投射到二维横向位置传感二极管（PSD）。通过使用LabVIEW开发的定制扫描器驱动模块和定制软件，以5 V幅值的正弦电压驱动扫描器。执行虚拟轴变换，使光纤尖端沿一条直线[11]运动。利用PSD测量光纤振动的方向，即该直线与水平轴之间的夹角 a。从显微镜测量得到光纤尖端轨迹长度的水平投影xh，结合该方向信息，可得出实际的光纤尖端偏转幅度xact，如以下公式所示：

$$
x_{act} = \frac{x_h}{2 \cos(\alpha)} \tag{4}
$$

3.1 光纤长度

由于该系统可简化为一个悬臂，因此缩短光纤长度预计会减小光纤尖端偏转，并提高系统的共振频率。目前，扫描器主要通过手动组装。因此，压电管与光纤之间的粘接接头以及系统中的结构阻尼在不同扫描器之间存在差异，导致按照相同设计组装的两个扫描器其光纤尖端偏转相差高达 28%。每次改变粘接接头时，都需要重新调整模型中的阻尼，以获得准确的光纤尖端偏转估计值。需要注意的是，阻尼的变化不会影响模型对共振频率估计的精度。为了避免改变粘接接头，通过从自由端切割来改变光纤悬臂的长度。切割操作是通过固定光纤尖端，然后使用金刚石刀头切割笔沿光纤指定位置进行穿透实现的。由于切割是在原位进行的，因此不会影响包括粘接接头在内的系统其余部分。

3.2 光纤直径

显著影响扫描光纤系统机械动力学的部分是光纤的悬臂部分。因此，只需改变该部分光纤的直径即可比较不同的光纤扫描器设计。保持其余部分光纤直径的标准性，可使扫描器组装过程不受设计变更的影响，并允许使用 commercially available 光纤和连接器。本小节中的光纤直径通过光纤蚀刻工艺以非常受控的方式进行变化。这里，我们将蚀刻比例参数f定义为公式(5)，其中lf 1为未蚀刻部分长度，lf 2为蚀刻部分长度，如图5所示。

$$
f = \frac{l_{f2}}{l_{f1} + l_{f2}} \times 100\% \tag{5}
$$

4 制造

我们实验室之前的研宄工作已经展示了光纤扫描仪的微加工技术[12,18]。从那时起，制造设备和技术都取得了显著进展。已开发出一种用于制造蚀刻光纤的自动化光纤蚀刻站。该装置（见图6）包含基于暗场照明的成像光学系统，通过斜射光线照射光纤以确定光纤的起始位置并跟踪蚀刻过程；两个轴上的电机移动系统；以及一台个人计算机，通过 LabVIEW控制电机的移动，并在显示窗口中测量光纤的当前直径。自动蚀刻基于

基于光纤在蚀刻溶液中浸泡时间越长，其直径越小的事实。此处我们近似假设为线性蚀刻速率，即蚀刻速率不受光纤直径变化的影响。

定制蚀刻液由49%氢氟酸(HF)溶液和6:4缓冲氧化物蚀刻液混合而成，以实现均匀表面光洁度。由熔融石英制成的光纤包层以一定的蚀刻速率进行径向蚀刻。使用抗氢氟酸腐蚀的微型蓝宝石比色皿作为蚀刻池。通过构建多层溶液结构，可实现阶梯蚀刻光纤、光纤锥及非线性轮廓[12]的制备。本研究重点在于制备具有光滑表面质量的高度一致的阶梯蚀刻光纤悬臂。对于阶梯蚀刻光纤，在混合HF溶液上方添加一层异辛烷，原因有多个。致密的异辛烷层充当缓冲层，并提供更好的蚀刻表面。若无异辛烷顶层，HF溶液将产生腐蚀性蒸气，可能导致光纤表面产生凹坑，并对操作人员造成暴露风险。

蚀刻准备包括光纤剥离和清洗以及蓝宝石比色皿的彻底清洁。机械剥离是通过使用特定切割工具切割覆盖在光纤包层上的涂层并将其拉出，这可能会在包层上留下一些凹痕。因此，我们采用化学剥离方法，将光纤浸入丙酮溶液中约4分钟，以软化涂层材料，然后轻轻剥离涂层。使用丙酮、异丙醇和去离子水对剥离后的光纤冲洗三次，以初步清除灰尘或污渍。然后使用射频清洁器清除之前清洗步骤可能遗留的有机残留物。将蓝宝石比色皿浸入由硫酸和过氧化氢按4:1比例混合而成的 piranha溶液中15分钟进行清洗，随后用丙酮、异丙醇和去离子水冲洗干净。

每次蚀刻过程开始时，先对测试光纤进行10分钟的蚀刻，然后取出测量蚀刻速率。蚀刻速率可能随蚀刻溶液的混合比例和纯度、光纤表面清洁度、室温、湿度和压力等因素而变化。因此，每次蚀刻前都必须测量蚀刻速率。测得的蚀刻速率以及包括蚀刻直径、蚀刻长度、额外蚀刻长度在内的设计参数

输入到LabVIEW程序中。预计蚀刻时间将由程序给出，并根据蚀刻速率和设计尺寸控制电机的移动。

为了确保尖端的几何形状正确以及蚀刻长度准确，蚀刻光纤悬臂长度比所需长度更长，多余部分随后被去除。蚀刻光纤的测量与切割是在定制的Bio‐Rad剪切显微镜（仪器编号 M411961，英国制造）上完成的，该显微镜配备了一个切割装置，可实现对蚀刻光纤直径和长度的精确测量与切割，参见图7中的设置。采用定制夹具固定光纤两端以施加适当的张力。机械切割器由超声信号驱动，产生振动在切割位置形成刻痕，然后施加增加的张力将光纤拉断。

阶梯式蚀刻光纤的制备结果可通过蚀刻部分的长度误差、直径和表面粗糙度来表征。影响蚀刻光纤尺寸误差的因素存在于准备阶段、蚀刻阶段以及切割阶段。在准备阶段，污渍可能附着在光纤上，这可能是由于光纤或比色皿清洁不彻底、蚀刻溶液本身含有杂质，或清洁后暴露于脏污环境中所致。在蚀刻过程中，直径测量时的观测误差可能导致不精确的蚀刻速率。实验台的移动会引起蚀刻溶液中的振动，以及房间内温度、湿度和压力的变化，这些也会影响蚀刻速率。在切割阶段，切割精度和切割区域质量可能存在差异。为了尽量减少这些复杂因素带来的变化，采取了彻底清洁、选择合适的房间进行蚀刻过程、蚀刻开始后避免与实验台接触，以及提高研究人员的测量和切割技能等措施。

测量装置精度为直径 0.1 μm，长度 0.001 mm。然而，测量过程中的人为误差可能更大。根据重复测量结果的差异，由于对监视器上显示的边缘判断不同，导致直径存在约 ±0.3 μm 的不确定性。长度测量受到图5中所示锥形部分的影响，因其难以确定可靠且可重复的起始点，从而引起不确定性，有时长度上的不确定性可高达 ±0.025 mm。

5 结果与讨论

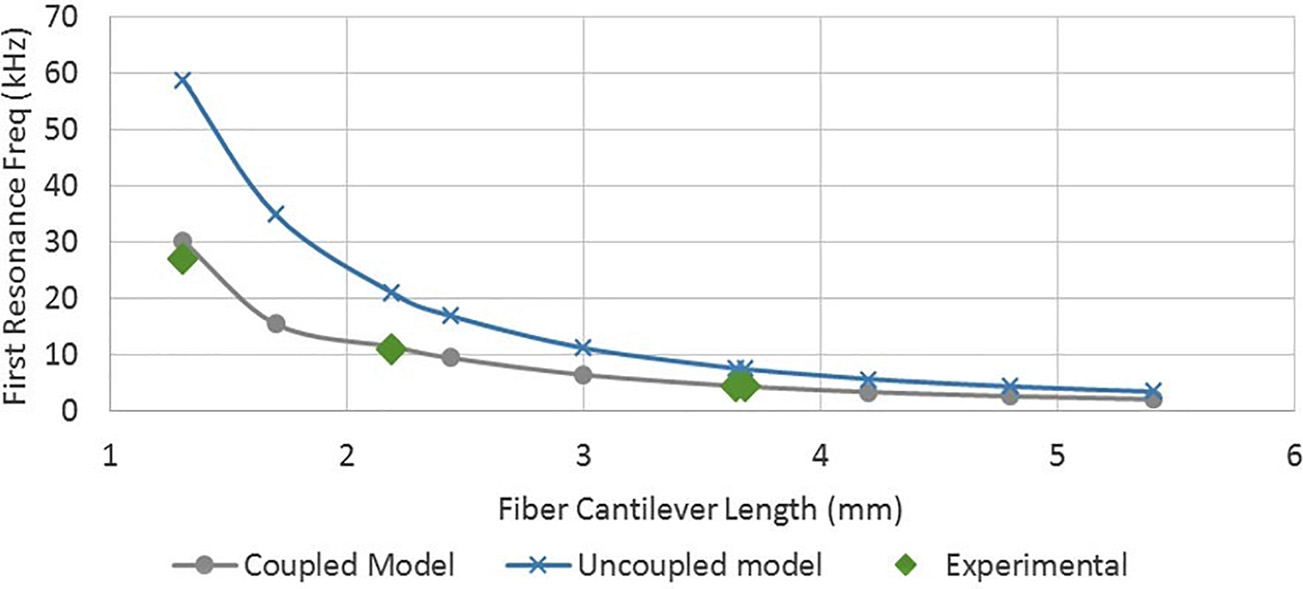
图8比较了本文提出的耦合模型与一种更简单的非耦合欧拉‐伯努利梁理论模型在预测共振频率方面的精度。根据基于梁理论的非耦合模型，圆形截面悬臂的一阶共振频率 $ f_{res} $ 由公式 (6)[19],给出，其中 $ d $ 和 $ L $ 分别为悬臂光纤的直径和长度，$ E $ 为杨氏模量，$ \rho $ 为密度，$ A $ 为横截面积，$ I $ 为截面惯性矩

$$
f_{res} = \frac{1.8752}{2\pi} \sqrt{\frac{EI}{\rho AL^4}} = 0.8789 \frac{d}{L^2} \sqrt{\frac{E}{\rho}} \tag{6}
$$

如图8所示，共振频率估计的误差随着悬臂长度的减小而增大。当光纤悬臂长度小于1.5毫米时，非耦合模型的共振频率估计误差高达98%，而耦合模型相对于实验数据点的误差仅上升至12%。

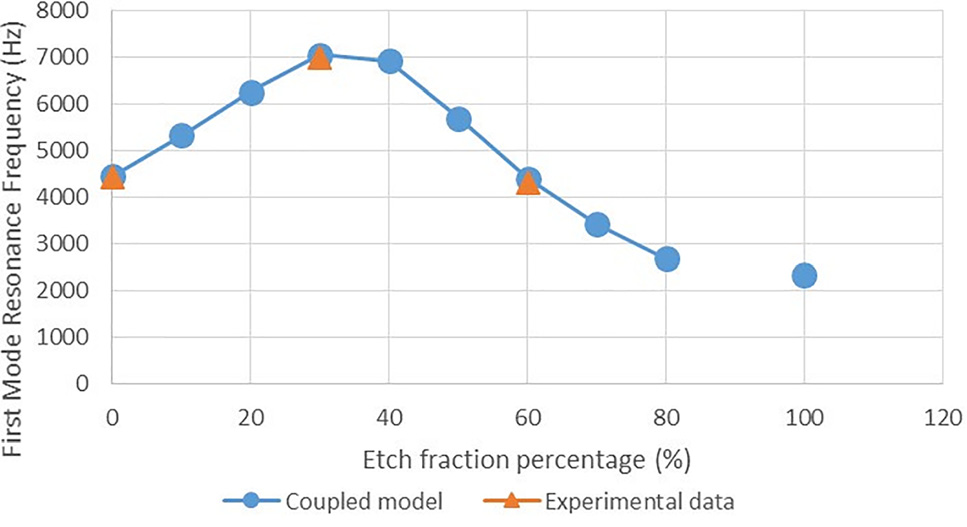
为了同时提高共振频率和光纤尖端偏转幅度，增加蚀刻比例 $ f $，由于光纤变得更柔性，从而导致更大的光纤尖端偏转，见图9。基于悬臂的欧拉‐伯努利梁模型可知，当直径减半时，共振频率也会减半。这一点在图9中0%和100%蚀刻比例的数据点处可以观察到。在这两点之间，无论是在仿真还是实验中，共振频率均表现出一个最大值，并在两侧出现滚降。这是因为光纤的 $ l_{f1} $ 和 $ l_{f2} $ 段均为具有各自共振频率的悬臂，且两者相互耦合。当蚀刻比例为0%时，$ l_{f2} $ 段的共振频率理论上为无穷大，而整个光纤的最大振幅偏转将出现在 $ l_{f1} $ 段的共振频率处。随着蚀刻比例的增加，$ l_{f1} $ 段会变短，因此该段的共振频率会上升，而 $ l_{f2} $ 段则变长，其共振频率随之下降。当蚀刻比例达到某一值时，$ l_{f2} $ 段最终变得足够长，使得 $ l_{f2} $ 段的共振频率小于 $ l_{f1} $ 段的共振频率，此时共振

$ l_{f2} $ 段的频率将使光纤尖端产生最大偏转。如果蚀刻比例进一步增加，此时一阶共振频率由 $ l_{f2} $ 决定，继续增加蚀刻比例会降低一阶共振频率。

因此，通过采用耦合模型仿真、光纤蚀刻和光纤切割，可以设计、制造和组装具有更高共振频率和更大光纤尖端偏转的光纤扫描器，从而实现更优的成像性能。此外，这种基于模型的设计过程能够对这两个参数进行更独立的控制。表 1总结了该过程：从总光纤悬臂长度为3.68 mm的基准光纤扫描器开始。从表1中的模型A（基准）到第一个设计模型B，显示了通过蚀刻提高共振频率和光纤尖端偏转的效果。由图9可知，对于给定的蚀刻后直径，通过蚀刻所能达到的共振频率存在一个上限。第二个阶梯蚀刻设计（表1中的模型C）

通过切割蚀刻光纤的一部分，实现了更高的共振频率。尽管光纤尖端偏转有所下降，但该设计在实现接近两倍共振频率的同时，与基准相比仍保持了偏转性能的提升。此外，在最大振幅下，阶梯蚀刻设计（模型B）相对于水平光轴的自由端角度高于直悬臂光纤扫描器（模型A）。表1还显示，耦合模型能够对共振频率（误差在2%以内）和尖端偏转（误差在12%以内）提供高度准确的估计，这有助于通过仿真评估光纤扫描器设计而无需每次都进行实验验证，从而实现更高效的设计迭代。虽然并非表1中的相同模型B光纤扫描器，图10展示了阶梯蚀刻微光扫描器的振动轮廓。

6 结论

本文中，我们开发了一种压电驱动共振光纤扫描器的高保真机电耦合有限元模型，该模型可对光纤悬臂的一阶共振频率进行模拟，误差小于12%，优于现有方法（误差可达98%）。我们还开发了用于光纤蚀刻的半自动微加工平台与工艺流程。通过制造并测试多种阶梯蚀刻光纤扫描器的创新设计，进一步验证了模型精度，并展示了模型驱动设计与制造的可行性与可靠性。

在未来工作中，我们将研究该模型在模拟具有更复杂几何结构的光纤悬臂扫描性能方面的能力。此外，我们将利用这种机电耦合有限元模型，为完整的SFE内窥镜提供具有期望共振频率、光纤偏转幅度和透镜设计的光纤悬臂设计。

计算）更准确，尤其是在光纤长度较 短时。)

表1	三种不同光纤扫描仪设计的一阶共振频率和尖端偏转幅度（距光轴的位移）的实验测量值(Expt)与耦合模型预测值(Sim)的比较
模型	设计
A基线3.68毫米
B 蚀刻 36%
C切离0.63毫米