背包问题总结

原创已于 2025-01-20 07:32:27 修改 · 137 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

于 2025-01-15 17:12:10 首次发布

蓝桥杯C/C++程序设计同时被 3 个专栏收录

128 篇文章

订阅专栏

模板

20 篇文章

订阅专栏

背包

3 篇文章

订阅专栏

心得：

背包问题就是关于物品不同件数（一件、多件、无穷件）或多组物品求一定体积下的最大价值

背包问题就是关于物品不同件数（一件、多件、无穷件）求一定体积下的最大价值

01背包

背包问题的数组除了背包都是一维度

//01背包基本模型
//特征：
//背包体积为m 物品个数为n 
//每个物品由体积和价值且有一个
//问题：求再当前体积v下能获得的最大价值
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+9;
//dp[i][j]:前i件物品能够获得的最大值
int dp[N][N];
int w[N],v[N];
//物品件数 背包体积 最大价值
int main()
{
  int n,m;cin>>n>>m;
  memset(dp,0,sizeof(dp));
  for(int i=1;i<=n;i++)
  {
    cin>>w[i]>>v[i];
  }
  for(int i=1;i<=n;i++)
  {
    for(int j=1;j<=m;j++)
    {
      if(j>=w[i])dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
      else dp[i][j]=dp[i-1][j];
    }
  }
  cout<<dp[n][m]<<endl;
  return 0;
}

【自制】01背包问题算法动画讲解_哔哩哔哩_bilibili

01背包优化

//01背包优化降维模型
//特征：一个维度
//背包体积为m 物品个数为n 
//每个物品由体积和价值且有一个
//问题：求再当前体积v下能获得的最大价值
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+9;
//dp[i][j]:前i件物品能够获得的最大值
int dp[N];
//物品件数 背包体积 最大价值
int main()
{
  int n,m;cin>>n>>m;
  //memset(dp,0,sizeof(dp));  初始条件为0，是否初始化均可
  for(int i=1;i<=n;i++)
  {
    int w,v;cin>>w>>v;
    for(int j=m;j>=w;j--)//反向更新
    {
     dp[j]=max(dp[j],dp[j-w]+v);
    }
  }
  cout<<dp[m]<<endl;
  return 0;
}

【动态规划秘籍】01背包、一维数组优化、完全背包，一网打尽！_哔哩哔哩_bilibili

完全背包

//完全背包正向更新
//完全背包和01优化背包只有再更新的方式上有区别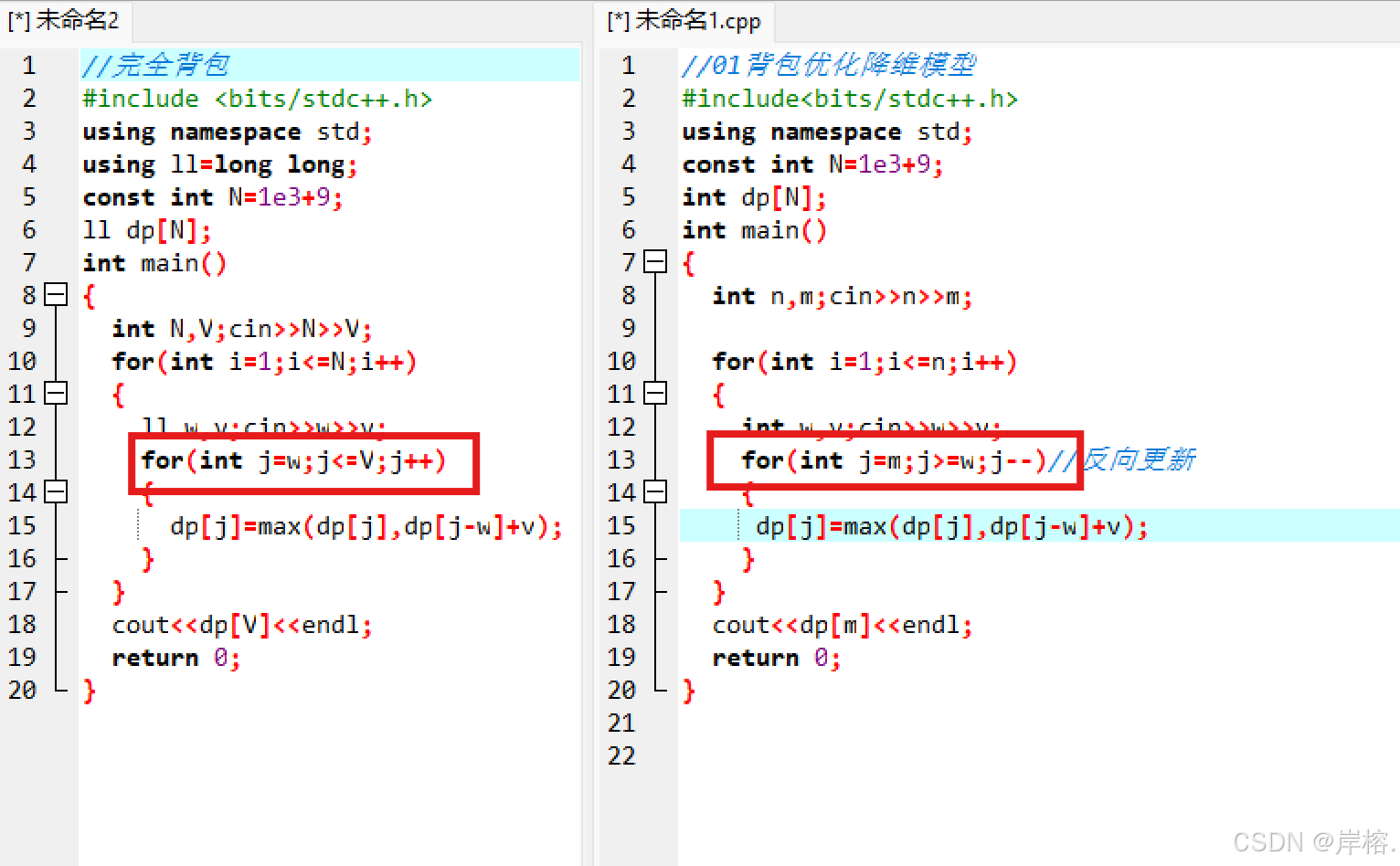

//完全背包之所以是这样的遍历方式就是因为只要价值最大怎么选择都可以 
//而01背包优化之后必须从前往后是因为每件物品只能选择一次 
//根本原因就是物品的件数不同

#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e3+9;
ll dp[N];
int main()
{
  int N,V;cin>>N>>V;
  for(int i=1;i<=N;i++)
  {
    ll w,v;cin>>w>>v;
    for(int j=w;j<=V;j++)
    {
      dp[j]=max(dp[j],dp[j-w]+v);
    }
  }
  cout<<dp[V]<<endl;
  return 0;
}

多重背包

01优化背包的变化

开long long

//时间复杂度为O（w*v*s）
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=2e2+9;
ll dp[N];
int main()
{
  int n,m;cin>>n>>m;
  for(int i=1;i<=n;i++)
  {
    ll w,v,s;cin>>w>>v>>s;
    while(s--)//有s件，所以进行s次处理
    {
      for(int j=m;j>=w;j--)//这个循环表示对一件物品的处理
      { 
          dp[j]=max(dp[j],dp[j-w]+v); 
      }
    }
  }
  cout<<dp[m]<<endl;
  return 0;
}

多重背包二进制优化

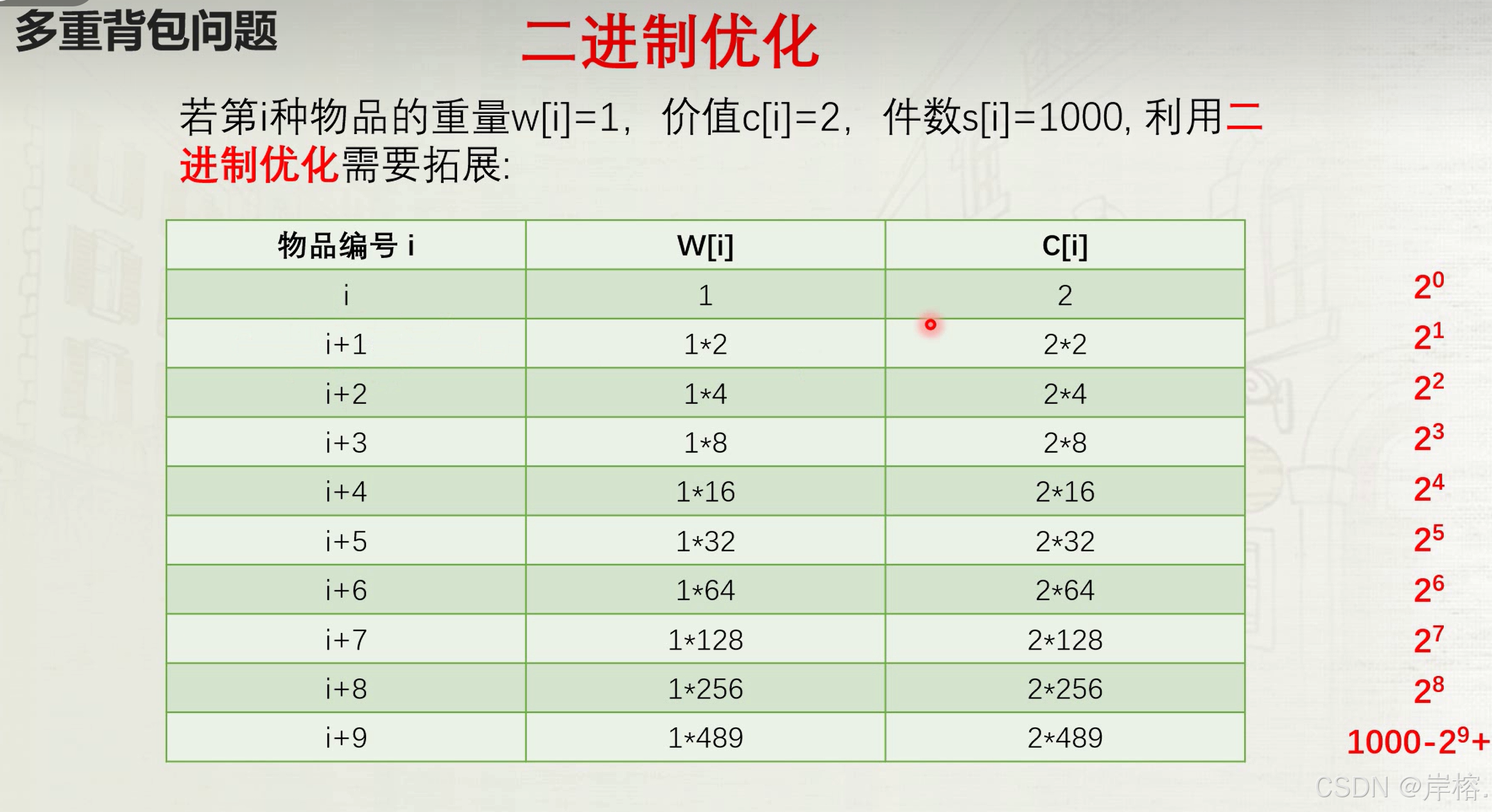
//时间复杂度O(n*v*log(s))
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e2+9;
ll dp[N];
int main()
{
  int n,m;cin>>n>>m;
  for(int i=1;i<=n;i++)
  {
    ll w,v,s;cin>>w>>v>>s;
    for(int k=1;k<=s;s-=k,k+=k)//k每次翻倍
    {
      for(int j=m;j>=k*w;j--)
      {
        dp[j]=max(dp[j],dp[j-k*w]+k*v);
      } 
    }
    //剩余的s个自动成为一组
    //将s个合并为1个;
    for(int j=m;j>=s*w;j--)
    {
      dp[j]=max(dp[j],dp[j-s*w]+s*v);
    }
  }
  cout<<dp[m]<<endl;
  return 0;
 }

易错点:

先是s-=k,然后k+=k；

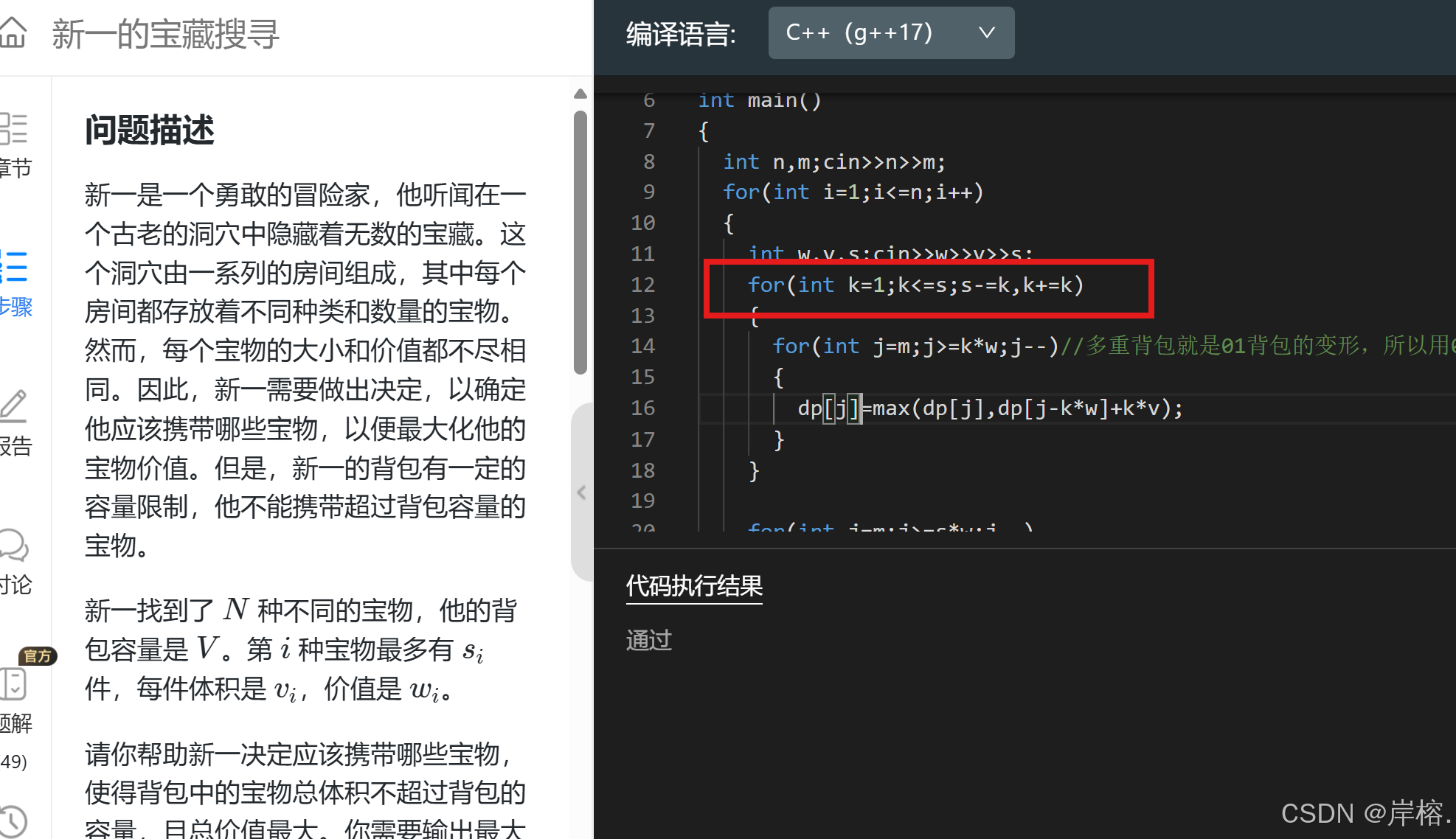
【重点！多重背包问题】二进制优化_哔哩哔哩_bilibili

二维费用背包

#include <bits/stdc++.h>
using namespace std;
using ll=long long;
//dp[j][k]体积为V，重量为M的背包
//相比于01优化背包维度仿照体积来
ll dp[105][105];
int main()
{
  int n,V,M;cin>>n>>V>>M;
  for(int i=1;i<=n;i++)
  {
    ll w,m,v;cin>>w>>m>>v;
    for(int j=V;j>=w;j--)
    {
      for(int k=M;k>=m;k--)
      {
        dp[j][k]=max(dp[j][k],dp[j-w][k-m]+v);
      }
    }
  }
  cout<<dp[V][M]<<endl;
  return 0;
}

多组背包

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int V=1e2+9;
const int N=1e2+9;
ll dp[N][V];
//dp[i][j]表示第i组物品体积为V的最大价值
int main()
{
  int n,m;cin>>n>>m;
 
  for(int i=1;i<=n;i++)
  {
    int s;cin>>s;
    for(int j=0;j<=m;j++)dp[i][j]=dp[i-1][j];//必须初始化
    while(s--)//每组里面选最优
    {//将每件物品依次选择
      ll w,v;cin>>w>>v;
      for(int j=w;j<=m;j++)
      {
        dp[i][j]=max(dp[i][j],dp[i-1][j-w]+v);
      }
    }
  }
  cout<<dp[n][m];
  return 0;
}