逃亡

最新推荐文章于 2024-08-27 09:45:20 发布

原创最新推荐文章于 2024-08-27 09:45:20 发布 · 428 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#分治法

分治法专栏收录该内容

7 篇文章

订阅专栏

本文探讨了甲乙两人如何利用自动小车实现从A地到C地的同时到达，且时间最短的问题。通过绘制示意图，采用二分法确定最佳下车点，确保二人能在E点相遇，实现最优化方案。

在这里插入图片描述
解析：
这道题实际上求的是甲（或者乙）从A地到C地所需的时间。
想要时间最短且同时到达，就要充分利用自动小车的特点，将示意图画下：

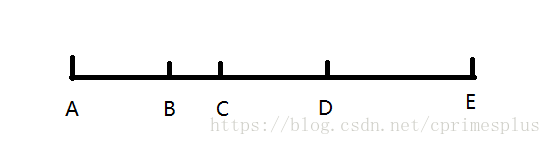
假设最初甲乙二人均在A点，那么最优方案就是：
甲从A点乘车出发，乙步行；甲到达D点时，开始下车步行，小车从D点返回去接正走到B点的乙，并且在C点与乙相遇；此时乙上车去追赶甲，且刚好在E点相遇。
由于路程是单调递增的，因此我们可以使用二分法来确定甲下车的具体位置，从而就可以计算出二人到达E点的时间。最初的起始位置自然是0，而终止位置是输入的AE间距离。通过二分法就可以很快确定下车位置。

代码：

#include<iostream>
#include <algorithm>
#include<cstdio>
#include<string>
#include<Windows.h>
#include<cstring>
#include<cmath>
#define MAXN 5000000
using namespace std;
int main()
{
	float len, step, car, st, mid, en;
	float t1, t2, t3, t4;
	cin >> len >> step >> car;
	st = 0;en = len;
	t1 = 0;t2 = 50;
	do
	{
		mid = (st + en) /2.0;
		t3 = mid / car;	//甲乘车到C的时间
		t1 = t3 + (len - mid) / step;	//甲到达终点的时间
		t4 = (mid - t3 * step) / (car + step);	//小车回来追甲的时间
		t2 = t3 + t4 + (len - (t3 + t4)*step) / car;	//乙乘车到达终点的时间
		if (t1 > t2)
			st = mid ;
		else 
			en = mid ;
	} while (fabs(t1 - t2) > 1e-4);
	cout << t1 << endl;
	system("pause");
	return 0;
}