魔法石的诱惑

解析：
想要完成这道题，首先要知道求n!有多少个0的计算方法。
最直观的方法就是计算出n!，然后迭代除以10，直到余数不为零为止。但是这样做显然会超时，并且对于较大数的阶乘，我们无法计算出它的值。
因此我们从分析n!的公式入手：


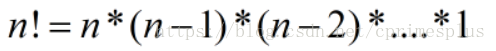
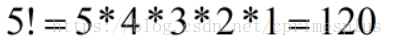
不难发现，一个数的阶乘想要末尾含有0，就要同时包括2的倍数和5的倍数（因为2*5=10）
又因为2的倍数比5的倍数多（因为是阶乘，含有5的倍数则一定含有2的倍数，反之则不一定），因此求n!末尾含有多少个0，实则就是求如下公式：

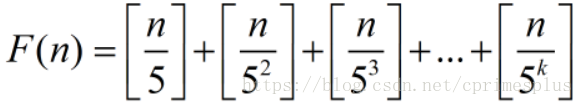
看到贴吧吧友问这个问题，突然意识到没写明白，这里是补充：
补充示例：

对于一个数，如果它是5^n的倍数，那么它可以拆分为n个5相乘，而这些5会和其他偶数结合，因此结尾会还会多0
故有代码：

int FindZero(int n)
{
	int cnt = 0;
	while (n)
	{
		cnt += n / 5;
		n /= 5;
	}
	return cnt;
}

因为随着n的增大，F(n)越来越大，满足单调关系，因此使用二分查找算法的效果显然更好，算法的时间复杂度为O(logN)
代码：

#include<iostream>
#include <algorithm>
#include<cstdio>
#include<string>
#include<Windows.h>
#include<cstring>
#define MAXN 50000
using namespace std;
int FindZero(int n)
{
	int cnt = 0;
	while (n)
	{
		cnt += n / 5;
		n /= 5;
	}
	return cnt;
}
int main()
{
	int n, aa;
	int mid, st, en;
	int ans = MAXN;
	cin >> n;
	st = 1;en = MAXN;
	while (st <= en)
	{
		mid = (st + en) >> 1;
		aa = FindZero(mid);
		if (aa == n) {
			ans = mid;
			break;
		}
		else if (aa < n)
			st = mid + 1;
		else
			en = mid - 1;
	}
	if (aa == MAXN) cout << "No Solution!" << endl;
	else {
		ans -= ans % 5;
		cout << ans << endl;
	}
	system("pause");
	return 0;
}