学习笔记-PyTorch-Softmax以及损失计算

1.Softmax实现概率分布

        分类器的主要功能是确定测试样本所属的类别。以图像识别为例，给定一张车辆的照片，分类器可以识别出该车辆是自行车、电动车还是普通汽车等具体类型。二分类问题是分类问题中最基本的形式，其输出只有两个类别，通常标记为0和1。之前的内容中介绍了线性模型实现二分类问题 。在这种情况下，如果样本属于类别0的概率是y，那么它属于类别1的概率就是1−y。因此，模型的输出是一维的，可以使用二元交叉熵损失（BCELoss）来计算损失值。

        然而，在大多数实际情况下，类别的数量往往不止两个。在多分类场景中，我们通常训练模型来输出样本属于每个类别的概率，然后根据这些概率进行排序，选择概率最高的类别作为模型的输出。如果继续使用二分类问题的线性模型思路，就会遇到问题。例如，如果类别1的概率 y1​ 是0.8，类别2的概率 y2​ 也是0.8，而类别3的概率 y3​ 是0.7，那么在决定样本的最终类别时就会出现矛盾。尽管 y1​ 和 y2​ 的概率最高，理论上应该选择这两个类别之一，但 y3​ 的概率也不低，同样有一定的可能性。这就是问题所在：我们希望模型的输出是一个明确的概率分布，能够反映样本属于各个类别的相对可能性。也就是说，每个类别都有一个对应的概率值，所有概率值之和为1。

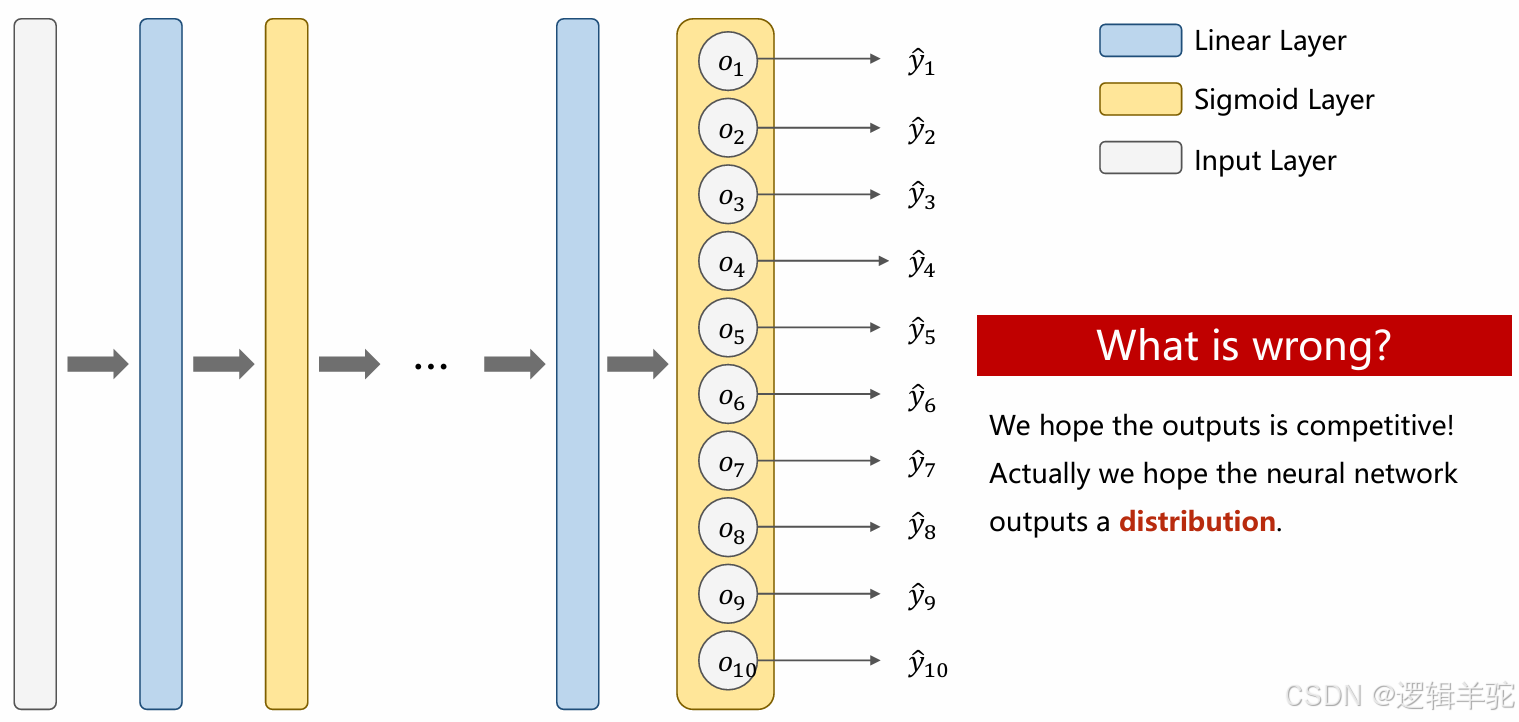
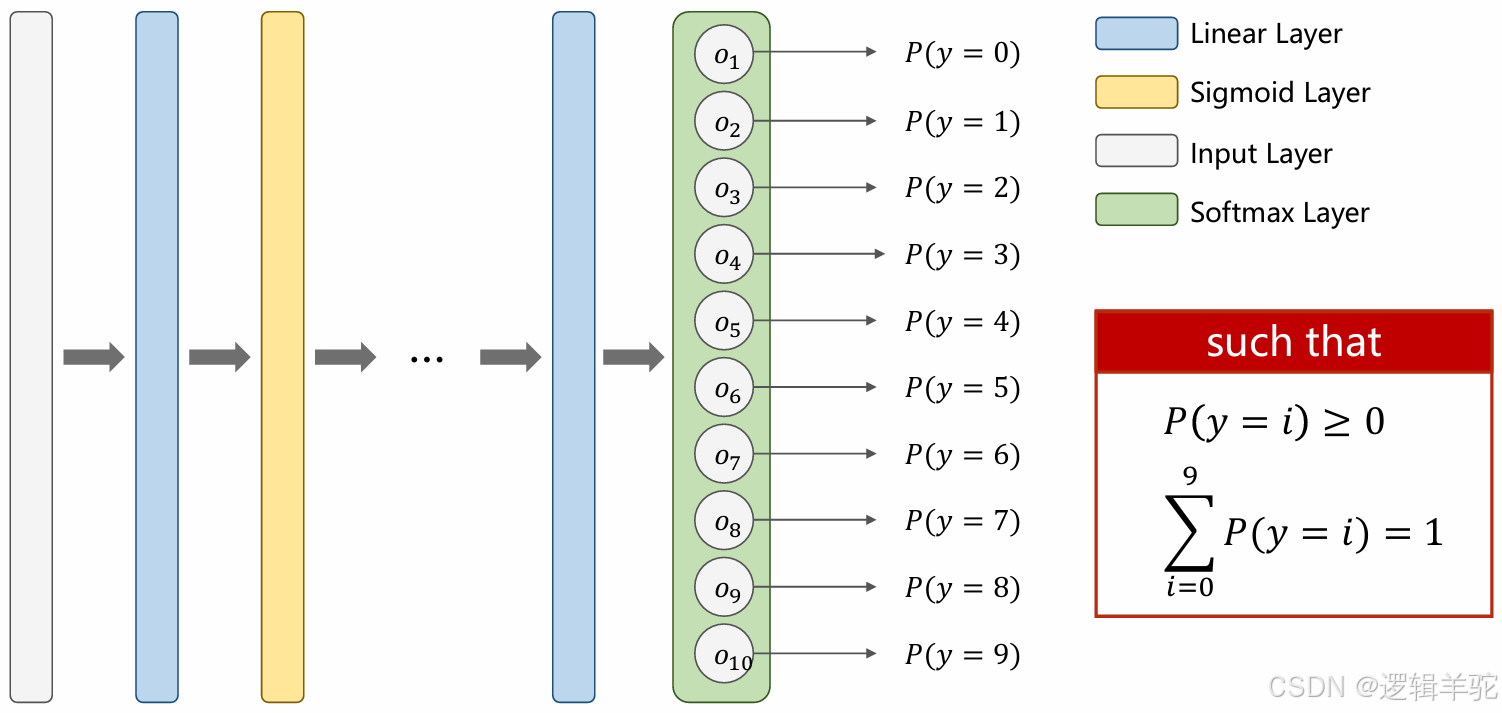
        采用Softmax函数将模型的原始输出（logits）转换为概率分布，Softmax计算公式为

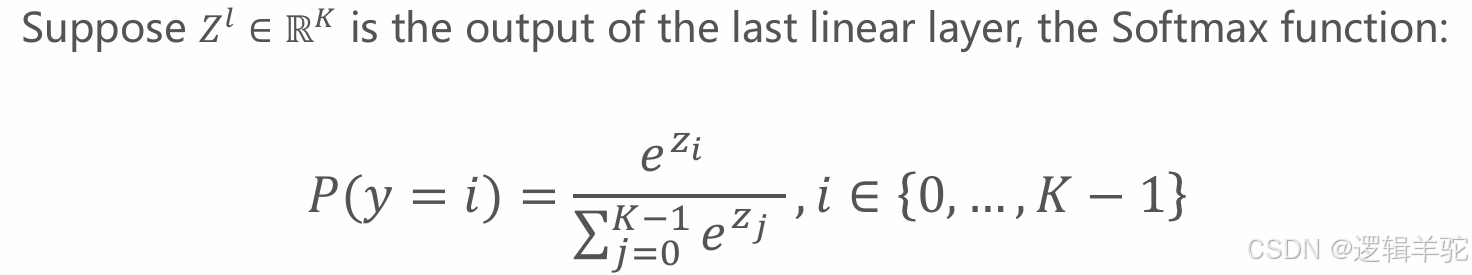
        使用框架如图所示：

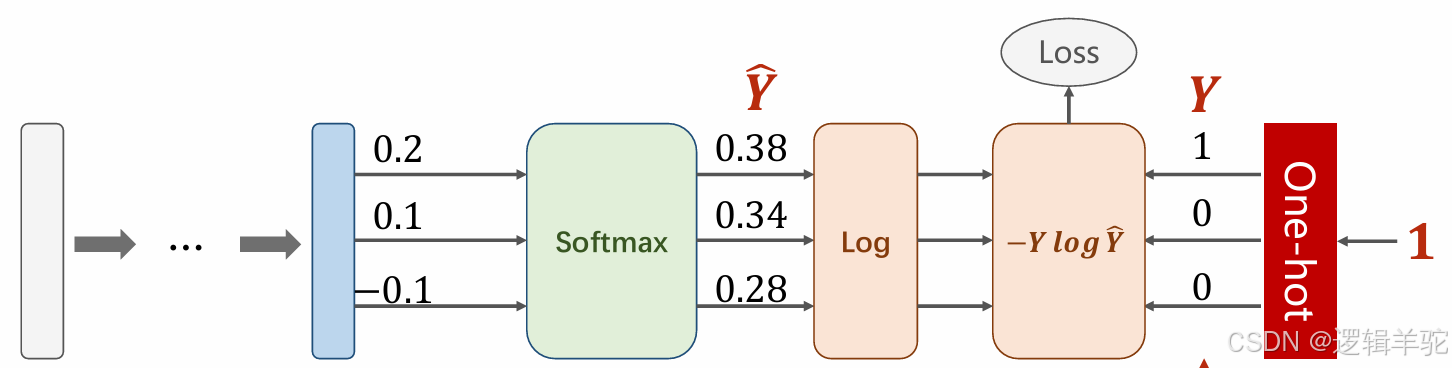
        对应代码如下所示，计算出来的损失值为0.9729

import numpy as np
y = np.array([1, 0, 0])
z = np.arr