洛谷P8815 [CSP-J 2022] 逻辑表达式

这个问题是让用C++实现对这种具有括号和优先级（&>I）的表达式的解析和计算，平时我们计算的表达式形式可以被称作中缀表达式，因为运算符号在数字的中间，比如

3+5*2，(3+5)*2

将中缀表达式转化成后缀表达式后，可以构建表达式树，以树状的结构完成对表达式值的计算

后缀表达式的计算方法：建立一个栈，从左到右遍历后缀表达式中的元素，如果是数字，就将其加入栈，如果是运算符，从栈顶取两个数进行该运算符对应的运算，将运算结果加入栈，最后栈中剩下的唯一一个元素就是表达式的值

例如 3+5*2=13转化到后缀表达式：3 5 2 * +

遍历第一个到第三个元素后，栈的状态：3 5 2

遍历到*时，计算5*2=10（注意顺序：5在运算符左侧，2在运算符右侧，虽然当前情况交换顺序没有影响，但是在本题下图的树中有影响），栈变为 3 10

遍历到+，计算3+10=13，结果就是13

将中缀表达式转化为后缀表达式：

中缀表达式中，含有的元素可能有：运算符（具有优先级，比如*>+），括号（左括号和右括号），数字

建立用来辅助完成转换的栈sta（stack）和用来记录转换结果（后缀表达式）的栈suf（suffix），从左到右遍历中缀表达式，遍历到当前元素值为x时：

如果x是数字，将其加入suf

如果x是左括号，将其加入sta

如果x是右括号，将sta中的元素不断弹出，直到遇到左括号，将左括号也从sta中弹出

如果x是运算符，若栈顶元素运算符的优先级（栈中此时只有可能含运算符和左括号）大于等于x，将sta栈顶元素运算符加入suf，从栈中弹出，继续判断新栈顶元素运算符与x的关系，继续加入suf弹出sta，遇见左括号的话停止，这之后将x加入sta

从左到右遍历中缀表达式结束后，如果sta中还有元素，依次弹出到suf

现在的思路是：将中缀表达式转成后缀表达式，用上述介绍的方法求后缀表达式的值，但是，实际上，求后缀表达式值的时候所用顺序和刚才介绍的方法不同，求后缀表达式的值是先建立表达式树，然后再从根开始递归计算，因为这样可以利用短路减少运算

比如0 1 0 | & 1 1 | 1 0 & | | 

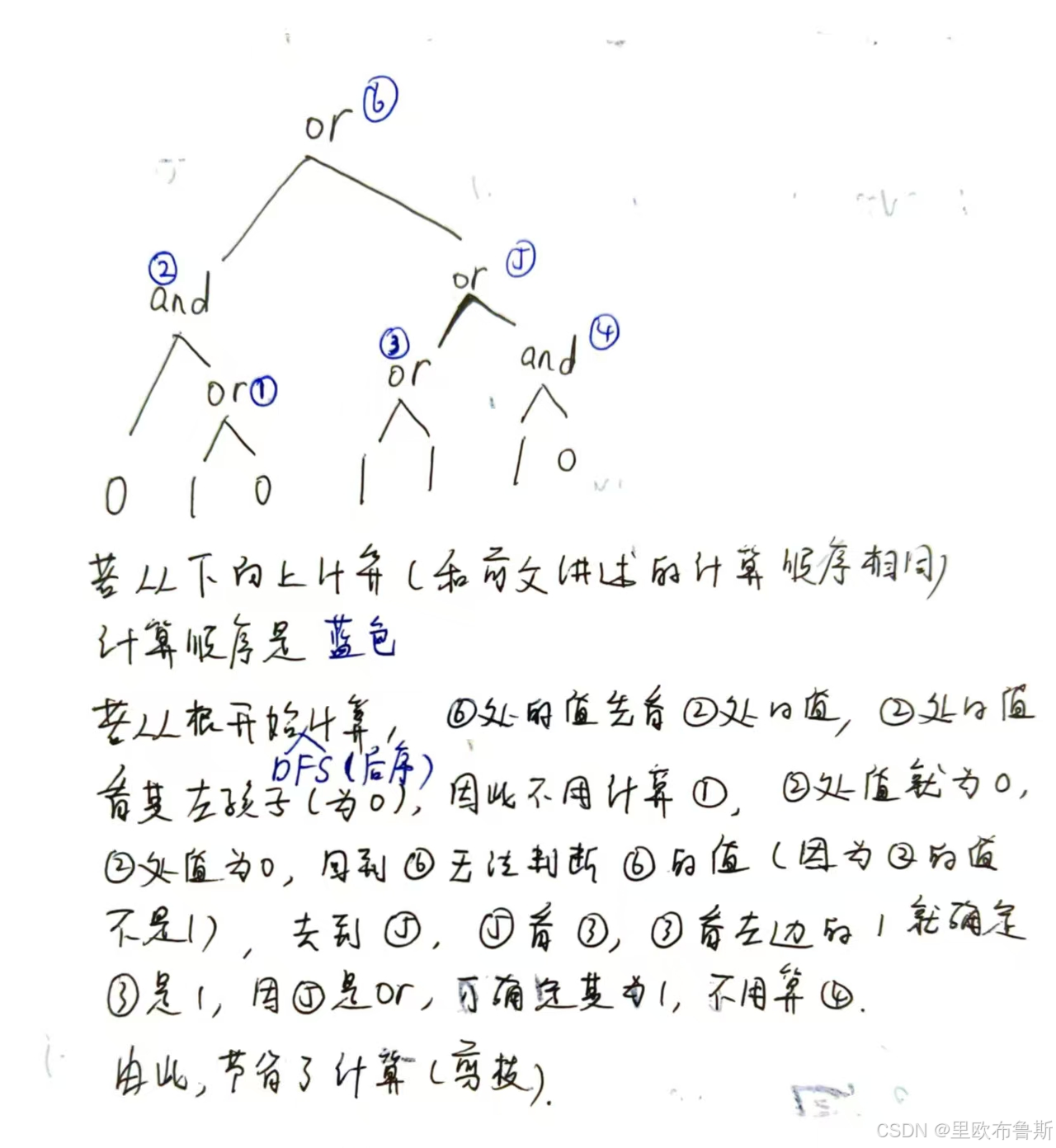
所以，统计的短路次数的时候要倒着进行dfs遍历树

注：这种计算中缀表达式值的问题，所用到的中缀表达式转后缀表达式，以及后缀表达式求值的方法暂且归结为特定算法，暂只熟悉算法，不讨论证明过程

#include<iostream>
#include<cstdio>
#include<stack>
#include<vector>
using namespace std;

const int maxn=1e6+5;

string s;
stack<char> sta;
vector<char> suf;
int cnt,ans1,ans2;

struct node{
    int l,r,v;
    node() : l(0), r(0), v(0) {}
    node(int x, int y, int z) : l(x), r(y), v(z) {}
}tree[maxn];

void build_tree(){
    stack<int> nodes;
    for(int i=0;i<suf.size();i++){
        if(suf[i]=='0' || suf[i]=='1'){
            tree[++cnt]=node(-1,-1,suf[i]-'0');
            nodes.push(cnt);
        }
        else if(suf[i]=='&'){
            int rs=nodes.top();nodes.pop();
            int ls=nodes.top();nodes.pop();
            int v;
            tree[++cnt]=node(ls,rs,2);
            nodes.push(cnt);
        }else if(suf[i]=='|'){
            int rs=nodes.top();nodes.pop();
            int ls=nodes.top();nodes.pop();
            tree[++cnt]=node(ls,rs,3);
            nodes.push(cnt);
        }
    }

}

int dfs(int u){
    if(tree[u].v==0 || tree[u].v==1) return tree[u].v;
    if(tree[u].v==2){       //&
        int ls=tree[u].l,rs=tree[u].r;
        if(dfs(ls)==0){
            ans1++;
            return 0;
        }else {
            return dfs(rs);
        }
    }else {
        int ls=tree[u].l,rs=tree[u].r;
        if(dfs(ls)==1){
            ans2++;
            return 1;
        }else {
            return dfs(rs);
        }
    }

}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);

    cin>>s;
    //中缀表达式转后缀表达式
    for(int i=0;i<s.size();i++){
        if(s[i]=='1' || s[i]=='0'){
            suf.push_back(s[i]);
        }else if(s[i]=='&'){
            while(!sta.empty() && sta.top()=='&'){
                suf.push_back('&');
                sta.pop();
            }
            sta.push('&');
        }else if(s[i]=='|'){
            while(!sta.empty() && sta.top()!='('){
                suf.push_back(sta.top());
                sta.pop();
            }
            sta.push('|');
        }else if(s[i]=='('){
            sta.push('(');
        }else if(s[i]==')'){
            while(sta.top()!='('){
                suf.push_back(sta.top());
                sta.pop();
            }
            sta.pop();
        }
    }
    while(sta.size()){
        suf.push_back(sta.top());
        sta.pop();
    }

    for(int i=0;i<suf.size();i++){
        cout<<suf[i]<<" ";
    }
    //建立表达式树
    build_tree();
    //dfs模拟求值
    cout<<dfs(cnt)<<"\n";
    cout<<ans1<<" "<<ans2<<"\n";
    return 0;
}