备战蓝桥杯---动态规划的一些思想2

最新推荐文章于 2025-11-24 14:56:02 发布

原创

最新推荐文章于 2025-11-24 14:56:02 发布 · 1.1k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #动态规划 #c++ #算法

文章讲述了如何通过两次深度优先搜索（DFS）和动态规划方法解决两个具体问题：一个是计算具有父子关系的树中某个节点的深度和，另一个是将数学问题转化为背包问题求解极大线性无关组。作者给出了对应的C++代码示例.

话不多说，直接看题：

1.换根DP：

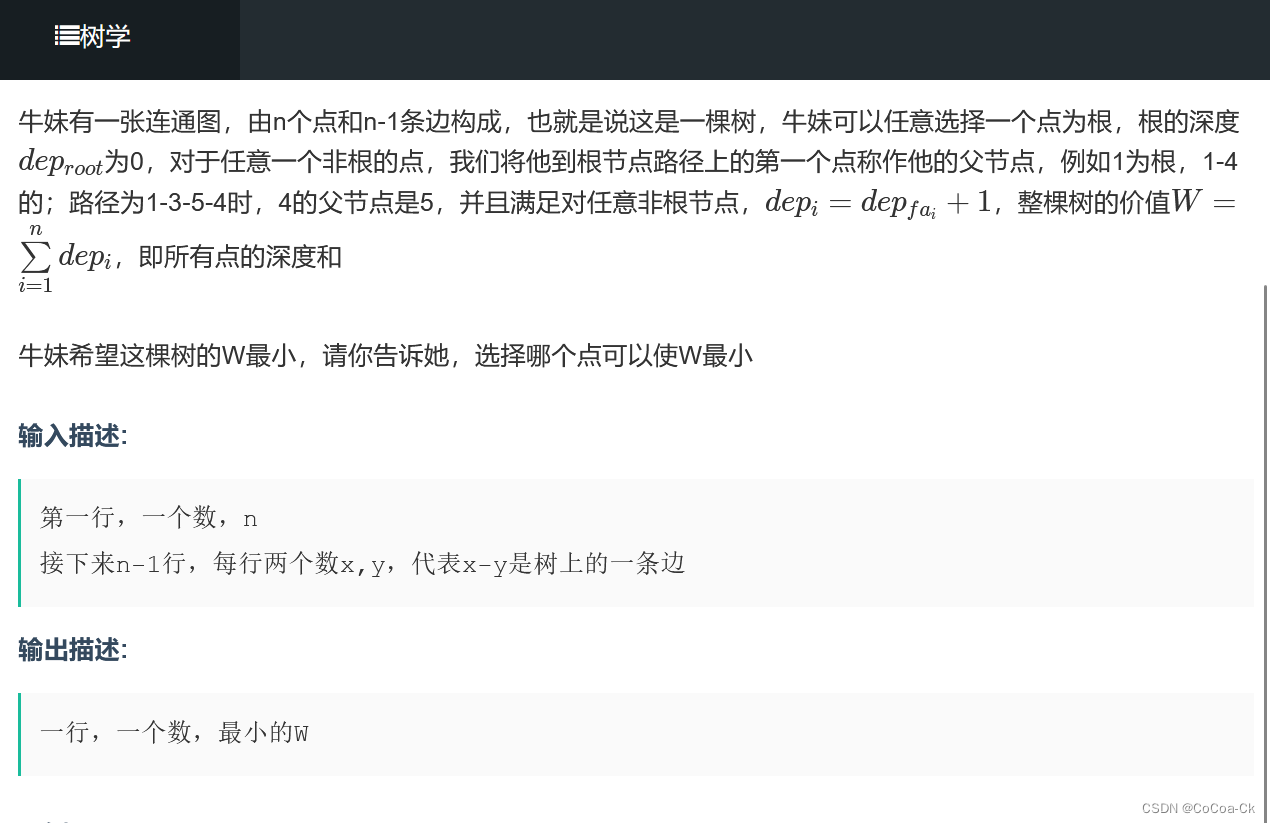
我们肯定不能对每一个根节点暴力求，我们不妨先求f[1]，我们发现当他的儿子作为根节点时深度和为f[1]+(n-cnt[i])-cnt[i](cnt[i]表示以i为根的节点数），这样子两遍DFS即可，下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,x,y,cnt[1000020],dep[1000010];
long long f[1000010];
vector<int> edge[1000010];
void dfs1(int root,int fa){
    cnt[root]=1;
    for(int i=0;i<edge[root].size();i++){
        int w=edge[root][i];
        if(w==fa) continue;
        dep[w]=dep[root]+1;
        dfs1(w,root);
        cnt[root]+=cnt[w];
    }
    return;
}
void dfs2(int root,int fa){
    for(int i=0;i<edge[root].size();i++){
        int w=edge[root][i];
        if(w==fa) continue;
        f[w]=f[root]+n-2*cnt[w];
        dfs2(w,root);
    }
    return;
}
int main(){
    cin>>n;
    for(int i=1;i<=n-1;i++){
        scanf("%d%d",&