光学相关MATLAB代码分享-1

1. 高斯光束等强度面作图

高斯光束是单色光在自由空间传播最简单的情况，其等强度面是单叶双曲面。下面是MATLAB绘图代码。假设波长λ=532 nm，束腰w0=0.5 mm。

clear;
% 高斯光束等强度比曲面画图
lambda=532; %波长/nm
w0=0.5; %束腰/mm
z0=pi*w0^2/lambda*1000; %rayleigh长度/m

z=-1:0.01:1; %z取值范围/m
w=@(z)w0*sqrt(1+(z/z0).^2); %相应的束宽w/mm
theta=linspace(0,2*pi,360);
[Z,Theta]=meshgrid(z,theta);
X=w(Z).*cos(Theta);
Y=w(Z).*sin(Theta);

mesh(Z,X,Y);
xlabel('传播距离\it{z}/m'); zlabel('束宽\it{w}/mm');
xlim([-1.2,1.2]); ylim([-1,1]); zlim([-1,1]);
set(gca,'ytick',[]);
view(315,15);
pbaspect([3,1,1]);

绘图结果：

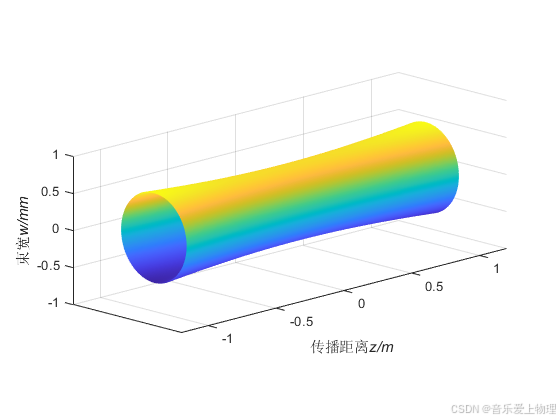
2.激光器F-P谐振腔的ABCD矩阵。

大部分激光器采用法布里-珀罗（F-P）谐振腔，F-P腔又可分为开放式（传统，最常见）和封闭式（对于光纤激光器和波导激光器）两类，前者由于侧壁对光不具约束能力，因此存在稳定性问题。该问题较为复杂，主要涉及到g因子和ABCD矩阵两个概念。下面通过高斯光束的q参数，来推导其ABCD矩阵。运行该代码要求MATLAB用户安装了符号计算工具箱。

clear;
% 高斯光束在谐振腔一个周期传输矩阵求解，即q5和q1的关系
% 基于分式线性函数的矩阵表示
syms R1 R2 L;   % 腔镜的曲率半径和腔长
syms M; % 一个周期的传输矩阵及其元素

M1=sym([1,L;0,1]);    % q1->q2 向右直线传播，原始方程为q2=q1+L
M2=sym([1,0;-2/R2,1]);% q2->q3 在腔镜R2反射，原始方程为1/q3=1/q2-2/R2
M3=sym([1,L;0,1]);    % q3->q4 向左直线传播，原始方程为q4=q3+L
M4=sym([1,0;-2/R1,1]);% q4->q5 在腔镜R1反射，原始方程为1/q5=1/q4-2/R1

M=M4*M3*M2*M1;
M=simplify(M);
pretty(M);

3.洛伦兹线形作图

洛伦兹展宽属于均匀展宽，起源于发光物体内粒子的碰撞，洛伦兹曾用阻尼谐振子模型进行了形象的解释。下面是该线形的MATLAB绘图代码。全部参数由用户输入。

clear;
% 归一化洛伦兹线形
% 由用户输入全部参数
nu0=input('输入本征频率f(THz)：');
dnu0=input('输入展宽(THz)：');
nu=linspace((nu0-4*dnu0),(nu0+4*dnu0),1000);
L=dnu0./((nu-nu0).^2+dnu0^2)/pi;

plot(nu,L,'b-'); hold on; grid on;
xlabel('\it{f}/THz'); ylabel('\it{L}(\nu)/THz^{-1}');
xlim([nu0-4*dnu0,nu0+4*dnu0]); ylim([0,max(L)]);

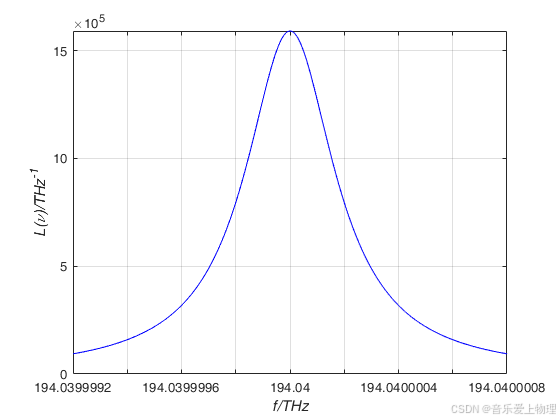
运行代码，按提示输入本征频率ν0=194.04 THz，展宽dν=2e-7 THz（参数取自TLB-6728激光器）。结果如下：