光学相关MATLAB代码分享-3

原创于 2024-11-19 12:41:54 发布 · 1.2k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

1.平板介质波导色散关系

3层平板介质波导是一种理想化的介质波导，由芯层（厚度为w）、衬底和包层构成。通常的正规波导仅假设器件沿传输z方向无限延伸，而平板波导还引入了沿横向（通常记为y）无限延伸的近似。波导的本征值方程为

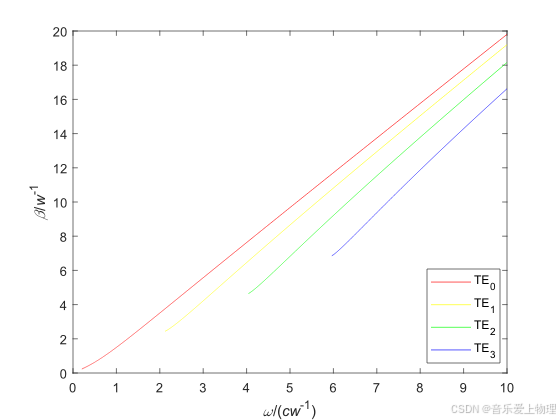
$\left( n_1^2-N^2 \right) ^{1/2} k_0 w=m\pi + \arctan{\left[ C_{12}\left(\frac{N^2-n_2^2}{n_1^2-N^2} \right) ^{1/2}\right ]} + \arctan{\left[ C_{13}\left(\frac{N^2-n_3^2}{n_1^2-N^2} \right) ^{1/2}\right ]}$

根据上式，下面给定厚度w，绘制波导TE0-3四个模式的传播常数-角频率（β-ω）关系图。设各层折射率分别为n1=2、n2=1.15、n3=1。为方便起见，这里β以1/w归一化，ω以c/w归一化，这样得到的横纵坐标都是无量纲的。

clear;
% TE_0~3模的beta-omega关系图。
n1=2;
n2=1.15;
n3=1;

% beta-omega为复杂的超越方程关系，给定任何一个求解另一个都很复杂。
% 但是，给定N=beta/k0=c*beta/omega，可以直接求得k0，进而求得beta和omega。
% 这是参数方程的思想。
N=linspace(n2,n1,1000); %有效折射率，这里作为参数

k0_inter=atan(sqrt((N.^2-n2^2)./(n1^2-N.^2)))+atan(sqrt((N.^2-n3^2)./(n1^2-N.^2)));
% 方程过于复杂，上面引入k0_inter为中间变量
% 下面为m=0~3阶模的k0。
% k0为归一化自由空间波数，实际为k0*w。k0的第m+1行存储了TE_m模的k0值。
for m=[0,1,2,3]
    if m==0
        k0(1,:)=k0_inter./sqrt(n1^2-N.^2);        
    else
        k0(m+1,:)=k0(1,:)+m*pi./sqrt(n1^2-N.^2);
    end
end

for m=[0,1,2,3]
    beta(m+1,:)=N.*k0(m+1,:); %beta为归一化传播常数，实际为beta*w。
end
omega=k0; %omega为归一化频率，实际为omega/c*w。

plot(omega(1,:),beta(1,:),'r-'); hold on;
plot(omega(2,:),beta(2,:),'y-'); hold on;
plot(omega(3,:),beta(3,:),'g-'); hold on;
plot(omega(4,:),beta(4,:),'b-'); hold on;
legend({'TE_0','TE_1','TE_2','TE_3'},'Location','best');
xlim([0,10]); xticks(0:1:10);
xlabel('\it{\omega}\rm{/(}\it{cw}\rm{^{-1})}'); ylabel('\it{\beta}\rm{/}\it{w}\rm{^{-1}}');

运行代码，得到如下曲线：

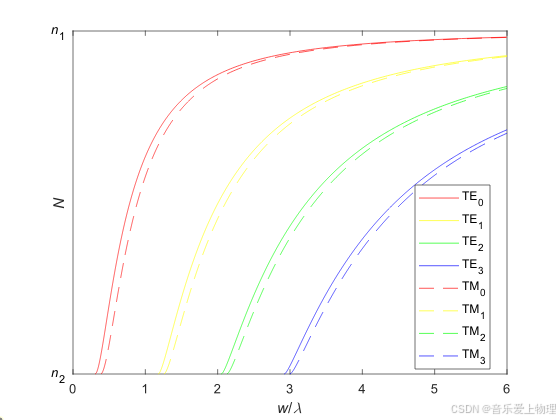
接下来绘制给定角频率ω（或真空波长λ），上述四个模式的有效折射率-芯层厚度（N-w）关系图。这里w以λ归一化。

clear;
%TE、TM的0~3阶模的N-w关系图
n1=1.62;
n2=1.515;
n3=1;

N=linspace(n2,n1,500); %有效折射率。由于给定w求解N为超越方程，所以给定N求解w。

w_interTE=atan(sqrt((N.^2-n2^2)./(n1^2-N.^2)))+atan(sqrt((N.^2-n3^2)./(n1^2-N.^2))); 
w_interTM=atan((n1/n2)^2*sqrt((N.^2-n2^2)./(n1^2-N.^2)))+atan((n1/n3)^2*sqrt((N.^2-n3^2)./(n1^2-N.^2)));
% 方程过于复杂，上面引入w_interT*为中间变量。
% 下面为m=0~3阶模的厚度。
% wT*为归一化厚度，实际为w/lambda。wT*的第m+1行存储了T*_m模的厚度值。
for m=0:1:3
    if m==0
        wTE(1,:)=w_interTE/2/pi./sqrt(n1^2-N.^2);
        wTM(1,:)=w_interTM/2/pi./sqrt(n1^2-N.^2);
    else
        wTE(m+1,:)=wTE(1,:)+m/2./sqrt(n1^2-N.^2);
        wTM(m+1,:)=wTM(1,:)+m/2./sqrt(n1^2-N.^2);
    end
end

plot(wTE(1,:),N,'r-'); hold on;
plot(wTE(2,:),N,'y-'); hold on;
plot(wTE(3,:),N,'g-'); hold on;
plot(wTE(4,:),N,'b-'); hold on;
plot(wTM(1,:),N,'r--'); hold on;
plot(wTM(2,:),N,'y--'); hold on;
plot(wTM(3,:),N,'g--'); hold on;
plot(wTM(4,:),N,'b--'); hold on;
legend({'TE_0','TE_1','TE_2','TE_3','TM_0','TM_1','TM_2','TM_3'},'Location','best');
xlim([0,6]); ylim([n2,n1]); % x轴（w）为0~5个波长，y轴（N）为n2~n1
xlabel('\it{w}\rm{/}\it{\lambda}'); ylabel('\it{N}');
xticks(0:1:6);
yticks([]); text(-0.05,0,'\it{n}\rm{_2}','sc'); text(-0.05,1,'\it{n}\rm{_1}','sc'); %手动设置y轴刻度

运行代码，得到如下曲线：

2.阶跃光纤色散关系

单包层圆形阶跃光纤是最简单的一种光纤。光纤纤芯（半径为a）和包层的折射率不随空间变化，分别记为n1和n2。光纤的归一化频率V定义为

$V^2=k_0^2\left( n_1^2-n_2^2 \right )a^2$

此外再定义两个重要的参数U、V

$U^2=\left(k_0^2 n_1^2-\beta^2 \right )a^2$

$W^2=\left(\beta^2-k_0^2 n_2^2 \right )a^2$

这三个参数满足U^2+W^2=V^2，它们在许多过程推导和结论中有重要作用。

下面绘制HE11，TE01，TM01，HE21，EH11，HE12六个模式的N-V色散曲线。设芯层和包层折射率分别为n1=1.62和n2=1.515。为方便起见，这里对U和V进行了变换：

$U^2=\frac{n1^2-N^2}{n1^2-n2^2}V^2$

$W^2=\frac{N^2-n2^2}{n1^2-n2^2}V^2$

这表明，当引入了归一化频率V后，阶跃光纤的色散性能仅和折射率有关，而和纤芯半径a无关。

clear all; close all;
%光纤的模式色散曲线（N-V关系）
%注意：TM模式为严格求解，而混合模式使用了弱导近似。
%U^2=(n1^2-N^2)/(n1^2-n2^2)*V^2，W^2=(N^2-n2^2)/(n1^2-n2^2)*V^2
n1=1.62; %芯层
n2=1.515;%包层

V_max=6;
V=0:0.01:V_max;
N_HE11=HEmn(V,n1,n2,1,1);
N_TE01=TE01(V,n1,n2);
N_TM01=TM01(V,n1,n2);
N_HE21=HEmn(V,n1,n2,2,1);
N_EH11=EHmn(V,n1,n2,1,1);
N_HE12=HEmn(V,n1,n2,1,2);

plot(V,N_HE11, V,N_TE01, V,N_TM01, V,N_HE21, V,N_EH11, V,N_HE12,'LineWidth',2);
xlim([0,V_max]); ylim([n2,n1]);
legend({'HE_{11}','TE_{01}','TM_{01}','HE_{21}','EH_{11}','HE_{12}'},'location','best');
xlabel('\it{V}');
ylabel('\it{N}\rm{_{eff}}');
set(gca,'FontName','Times New Roman','FontSize',15);

运行代码，得到如下曲线：

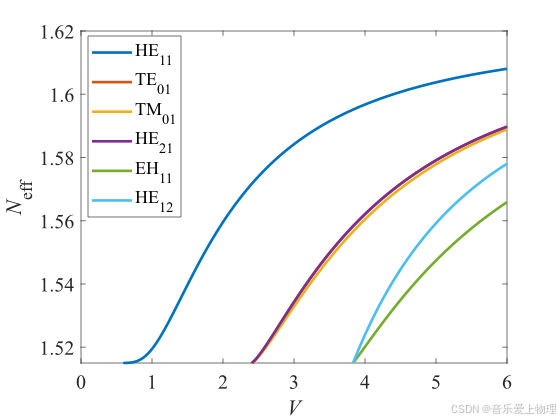
图中，2个近简并模式TE01和HE21发生了完全简并。这是由于混合模式采用了弱导近似。

该程序引用了4个自定义的函数：HEmn、EHmn、TE01、TM01，可以附在代码末尾，也可以单独成一个文件，与主程序放在同一目录下。

HEmn（使用了弱导近似）：

function N=HEmn(V,n1,n2,m,n)
%HE_mn模式的N-V关系
    disp(['正在计算HE_',num2str(m),num2str(n),'模式']);
    N_min=n2+0.00001; %有效折射率N的搜索下限是包层折射率n2，加0.00001以避免奇异性。
    i_max=length(V);
    N=zeros(1,i_max);
    n_count=1;
    N_1=0;
    for ii=1:i_max
        Vi=V(ii); %输入的V可以是向量，Vi是大循环中的当前V值。
        N_test=N_min : 0.00001 : n1-0.00001;
        U=sqrt((n1^2-N_test(1)^2)/(n1^2-n2^2)) * Vi;
        W=sqrt((N_test(1)^2-n2^2)/(n1^2-n2^2)) * Vi;
        result=besselj(m-1,U)/U/besselj(m,U) - besselk(m-1,W)/W/besselk(m,W);
        %待求特征方程即为result=0。
        ispositive_1=result>0;
        for jj=2:length(N_test)
            U=sqrt((n1^2-N_test(jj)^2)/(n1^2-n2^2)) * Vi;
            W=sqrt((N_test(jj)^2-n2^2)/(n1^2-n2^2)) * Vi;
            result=besselj(m-1,U)/U/besselj(m,U)...
                - besselk(m-1,W)/W/besselk(m,W);
            ispositive_2=result>0;
            N_2=0;
            if ispositive_2~=ispositive_1 %相邻2次小循环result正负反转，表明找到特征方程的解。
                N_2=(N_test(jj)+N_test(jj-1)) /2;
                if N_2<N_1
                    n_count=n_count+1;
                end
                if n_count==n
                    N(ii)=N_2; %输出当前Vi下的有效折射率N。
                    N_min=N(ii); %重新定义N的搜索下限，防止错误输出下一径向量子数n对应的N，并减少后续计算量。
                end
                break;
            end
            ispositive_1=ispositive_2;
        end
        N_1=N_2;
    end
end

EHmn（使用了弱导近似）：

function N=EHmn(V,n1,n2,m,n)
%EH_mn模式的N-V关系
    disp(['正在计算EH_',num2str(m),num2str(n),'模式']);
    N_min=n2+0.00001; %有效折射率N的搜索下限是包层折射率n2，加0.00001以避免奇异性。
    i_max=length(V);
    N=zeros(1,i_max);
    n_count=1;
    N_1=0;
    for ii=1:i_max
        Vi=V(ii); %输入的V可以是向量，Vi是大循环中的当前V值。
        N_test=N_min : 0.00001 : n1-0.00001;
        U=sqrt((n1^2-N_test(1)^2)/(n1^2-n2^2)) * Vi;
        W=sqrt((N_test(1)^2-n2^2)/(n1^2-n2^2)) * Vi;
        result=besselj(m+1,U)/U/besselj(m,U) + besselk(m+1,W)/W/besselk(m,W);
        %待求特征方程即为result=0。
        ispositive_1=result>0;
        for jj=2:length(N_test)
            U=sqrt((n1^2-N_test(jj)^2)/(n1^2-n2^2)) * Vi;
            W=sqrt((N_test(jj)^2-n2^2)/(n1^2-n2^2)) * Vi;
            result=besselj(m+1,U)/U/besselj(m,U)...
                + besselk(m+1,W)/W/besselk(m,W);
            ispositive_2=result>0;
            N_2=0;
            if ispositive_2~=ispositive_1 %相邻2次小循环result正负反转，表明找到特征方程的解。
                N_2=(N_test(jj)+N_test(jj-1)) /2;
                if N_2<N_1
                    n_count=n_count+1;
                end
                if n_count==n
                    N(ii)=N_2; %输出当前Vi下的有效折射率N。
                    N_min=N(ii); %重新定义N的搜索下限，防止错误输出下一径向量子数n对应的N，并减少后续计算量。
                end
                break;
            end
            ispositive_1=ispositive_2;
        end
        N_1=N_2;
    end
end

TE01：

function N=TE01(V,n1,n2)
%TE_01模式的N-V关系
    disp('正在计算TE_01模式');
    N_min=n2+0.00001; %有效折射率N的搜索下限是包层折射率n2，加0.00001以避免奇异性。
    i_max=length(V);
    N=zeros(1,i_max);
    for ii=1:i_max
        Vi=V(ii); %输入的V可以是向量，Vi是大循环中的当前V值。
        N_test=N_min : 0.00001 : n1-0.00001;
        U=sqrt((n1^2-N_test(1)^2)/(n1^2-n2^2)) * Vi;
        W=sqrt((N_test(1)^2-n2^2)/(n1^2-n2^2)) * Vi;
        result=besselj(1,U)/U/besselj(0,U) + besselk(1,W)/W/besselk(0,W);
        %待求特征方程即为result=0。
        ispositive_1=result>0;
        for jj=2:length(N_test)
            U=sqrt((n1^2-N_test(jj)^2)/(n1^2-n2^2)) * Vi;
            W=sqrt((N_test(jj)^2-n2^2)/(n1^2-n2^2)) * Vi;
            result=besselj(1,U)/U/besselj(0,U)...
                + besselk(1,W)/W/besselk(0,W);
            ispositive_2=result>0;
            if ispositive_2~=ispositive_1 %相邻2次小循环result正负反转，表明找到特征方程的解。
                N(ii)=(N_test(jj)+N_test(jj-1)) /2; %输出当前Vi下的有效折射率N。
                N_min=N(ii); %重新定义N的搜索下限，防止错误输出下一径向量子数n对应的N，并减少后续计算量。
                break;
            end
            ispositive_1=ispositive_2;
        end
    end
end

TM01（可以使用弱导近似，但是这里采用了严格求解）：

function N=TM01(V,n1,n2)
%TM_01模式的N-V关系
    disp('正在计算TM_01模式');
    N_min=n2+0.00001; %有效折射率N的搜索下限是包层折射率n2，加0.00001以避免奇异性。
    i_max=length(V);
    N=zeros(1,i_max);
    for ii=1:i_max
        Vi=V(ii); %输入的V可以是向量，Vi是大循环中的当前V值。
        N_test=N_min : 0.00001 : n1-0.00001;
        U=sqrt((n1^2-N_test(1)^2)/(n1^2-n2^2)) * Vi;
        W=sqrt((N_test(1)^2-n2^2)/(n1^2-n2^2)) * Vi;
        result=n1^2*besselj(1,U)/U/besselj(0,U) + n2^2*besselk(1,W)/W/besselk(0,W);
        %待求特征方程即为result=0。
        ispositive_1=result>0;
        for jj=2:length(N_test)
            U=sqrt((n1^2-N_test(jj)^2)/(n1^2-n2^2)) * Vi;
            W=sqrt((N_test(jj)^2-n2^2)/(n1^2-n2^2)) * Vi;
            result=n1^2*besselj(1,U)/U/besselj(0,U)...
                + n2^2*besselk(1,W)/W/besselk(0,W);
            ispositive_2=result>0;
            if ispositive_2~=ispositive_1 %相邻2次小循环result正负反转，表明找到特征方程的解。
                N(ii)=(N_test(jj)+N_test(jj-1)) /2; %输出当前Vi下的有效折射率N。
                N_min=N(ii); %重新定义N的搜索下限，防止错误输出下一径向量子数n对应的N，并减少后续计算量。
                break;
            end
            ispositive_1=ispositive_2;
        end
    end
end

3.波导的横向倏逝耦合

波导横向耦合是一类重要的光学问题。最简单的情况是两根波导均为正规波导，且耦合时平行放置。这种问题可以采用微扰法求解（传统且直观的方法），也可将整个耦合器视为一个整体，采用模式分裂和空间拍频的思路求解（更简洁，适合FEM模拟）。

下面采用微扰法，作图演示平行双波导发生耦合时，功率分布随传播方向z的变化（默认完全匹配；作图结果略）。

同向耦合：

clear;
% 耦合画图
d=INPUT('输入相位失配比例：',0); % d=Delta/Kc，默认完全匹配
a12=@(Kcz)(sin(sqrt(1+d^2)*Kcz)).^2/(1+d^2);
a22=@(Kcz)(cos(sqrt(1+d^2)*Kcz)).^2+(sin(sqrt(1+d^2)*Kcz)).^2/(1+1/d^2);

Kcz=linspace(0,2*pi,1000);
A12=a12(Kcz);
A22=a22(Kcz);

plot(Kcz,A12,'r-'); hold on;
plot(Kcz,A22,'b-');
set(gca,'FontName','Times New Roman','FontSize',13)
xlabel('\it{K}\rm{_c}\it{z}'); ylabel('\fontname{宋体} 模式功率相对值');
xlim([0,2.5*pi]); ylim([0,1.4]);
xticks(0:pi/2:pi*2); xticklabels({'0','\pi/2','\pi','3\pi/2','2\pi'}); yticks(0:0.2:1);
legend({'|\it{A}\rm{_1}(\it{z}\rm{)|^2}','|\it{A}\rm{_2}(\it{z}\rm{)|^2}'},'location','best');
box off;
ax1 = axes('Position',get(gca,'Position'),'XAxisLocation','top',...
    'YAxisLocation','right','Color','none','XColor','k','YColor','k');
set(ax1,'XTick', [],'YTick', []);
hold off;

function context=INPUT(display,default) %自定义带缺省的输入功能
    context=input(display);
    if isempty(context)
        context=default;
    end
end

反向耦合：

clear;
% 耦合画图
d=INPUT('输入相位失配比例：',0); % d=Delta/Kc，默认完全匹配
KcL=INPUT('输入相对长度：',5); % KcL=L*Kc，默认L=5/Kc

Kcz=linspace(0,KcL,1000);
A12=a12(Kcz,KcL,d);
A22=a22(Kcz,KcL,d);

plot(Kcz,A12,'r--'); hold on;
plot(Kcz,A22,'b:');
set(gca,'FontName','Times New Roman','FontSize',13)
xlabel('\it{K}\rm{_c}\it{z}'); ylabel('\fontname{宋体} 模式功率相对值');
xlim([0,KcL]); ylim([0,1.4]);
xticks(0:KcL/2:KcL); yticks(0:0.2:1);
xticklabels({'0','\it{K}\rm{_c}\it{L}\rm{/2}','\it{K}\rm{_c}\it{L}'});
legend({'|\it{A}\rm{_1}(\it{z}\rm{)|^2}','|\it{A}\rm{_2}(\it{z}\rm{)|^2}'},'location','best');
box off;
ax1 = axes('Position',get(gca,'Position'),'XAxisLocation','top',...
    'YAxisLocation','right','Color','none','XColor','k','YColor','k');
set(ax1,'XTick', [],'YTick', []);
hold off;

function a12=a12(Kcz,KcL,d)
    s=sqrt(1-d^2); % 定义无量纲中间变量，s=S/Kc
    a12=(sinh(s*(Kcz-KcL))).^2 ./...
        (d^2*(sinh(s*KcL)).^2 + s^2*(cosh(s*KcL)).^2);
end

function a22=a22(Kcz,KcL,d)
    s=sqrt(1-d^2); % 定义无量纲中间变量，s=S/Kc
    a22=(d^2*(sinh(s*(Kcz-KcL))).^2 + s^2*(cosh(s*(Kcz-KcL))).^2) ./...
        (d^2*(sinh(s*KcL)).^2 + s^2*(cosh(s*KcL)).^2);
end

function context=INPUT(display,default) %自定义带缺省的输入功能
    context=input(display);
    if isempty(context)
        context=default;
    end
end