1. 激光器洛伦兹展宽(碰撞展宽)和多普勒展宽比较图
在固体激光器中,碰撞展宽是主要因素。在气体激光器中,通常碰撞展宽也是主要因素,但是在特殊情况如低压或高温,多普勒展宽会逐渐明显,甚至成为主要因素。
下面的MATLAB程序,以CO2激光器为例,画出指定温度和压强下的洛伦兹和高斯线形。
clear;
% CO2气体激光器2种展宽对比
T=input('输入温度(K):');
p=input('输入压强(atm):'); p=p*1e5;
R=8.31451; k_B=1.380649e-23; c=299792458;
m_mol=0.044; sigma=5.03e-19; nu0=2.828e13; m=m_mol*k_B/R;
N=p/k_B/T;
%--洛伦兹
beta=N*sigma*sqrt(16*R*T/pi/m_mol); %阻尼系数
dnu0=beta/2/pi; %展宽尺度
nu=linspace(-4*dnu0,4*dnu0,1000);
L=dnu0./(nu.^2+dnu0^2)/pi;
FWHM_L=2*dnu0;
%--高斯
S=sqrt(m/2/pi/k_B/T)*c/nu0*exp(-m*c^2*nu.^2/2/k_B/T/nu0^2);
FWHM_S=2*nu0/c*sqrt(2*k_B*T/m*log(2));
disp(['碰撞(洛伦兹)展宽FWHM=',num2str(FWHM_L),newline,'多普勒(高斯)展宽FWHM=',num2str(FWHM_S)]);
plot(nu,L,'b-'); hold on; grid on;
plot(nu,S,'r-'); hold on;
xlabel('(\it{\nu}\rm{-}\it{\nu}\rm{_0)/Hz}'); ylabel('线形函数/Hz^{-1}');
xlim([-4*dnu0,4*dnu0]); ylim([0,max(L)]);
legend({'碰撞展宽\it{L}\rm{(}\it{\nu}\rm{)}','多普勒展宽\it{S}\rm{(}\it{\nu}\rm{)}'},'Location','best');
运行代码,在T=300 K,p=1 atm和T=600 K,p=0.3 atm和T=600 K,p=0.03 atm时,分别得到如下结果。
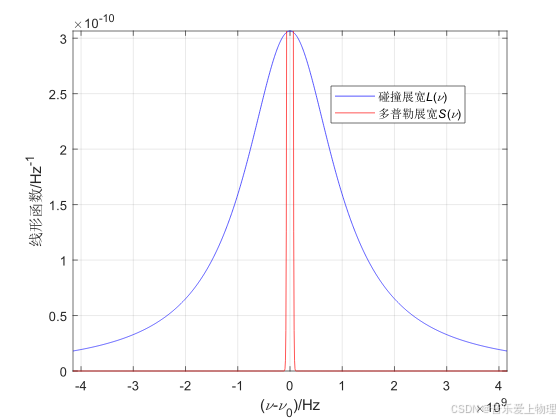
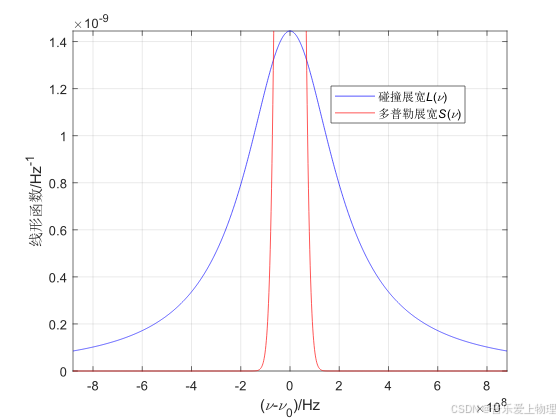
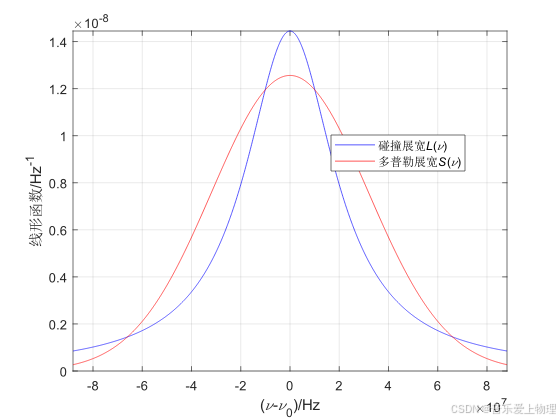
2.激光器频率牵引示意图
频率牵引是激光器的一个重要现象。它是指激光器实际频率总是介于介质本征频率和(真空下)谐振腔本征频率之间。这与我们的直觉相符,严格证明需要求解有限空间(即驻波情形)的Maxwell方程组。MATLAB动画演示程序如下。
clear;
% 频率牵引动画
nu0=input('输入介质频率(THz):'); nu0=nu0*1e12;
beta=input('输入阻尼系数β(ns-1):'); beta=beta*1e9;
g=input('输入增益g(m-1):');
c=299792458;
nun=linspace(nu0*0.9,nu0*1.1,200);
nu=(beta*nun+g*c*nu0/2)/(beta+g*c/2);
figure;
line([nu0,nu0],[0,1],'Color','green','LineStyle','-');
xlim([nu0*0.85,nu0*1.15]); ylim([0,1]);
xlabel('频率/THz');
yticks([]);
nun_line=line([nun(1),nun(1)],[0,1],'Color','blue','LineStyle','-');
nu_line=line([nu(1),nu(1)],[0,1],'Color','red','LineStyle','-');
legend({'介质频率\it{\nu}\rm{_0}','谐振腔频率\it{\nu_n}','实际频率\it{\nu}'},'Location','best');
pause(0.1);
for n=2:length(nun)
delete(nun_line); delete(nu_line);
nun_line=line([nun(n),nun(n)],[0,1],'Color','blue','LineStyle','-');
nu_line=line([nu(n),nu(n)],[0,1],'Color','red','LineStyle','-');
legend({'介质频率\it{\nu}\rm{_0}','谐振腔频率\it{\nu_n}','实际频率\it{\nu}'},'Location','best');
pause(0.1);
end
3.调Q激光器有关求解
调Q激光器,粒子数反转密度ΔN和光子流密度Φv的时间特性为:
这个常微分方程组无法解析求解,只能在给定初始条件下求出数值解。下面使用MATLAB的ode系列函数求解。代码中假设激光器的阈值增益gt=2.2e-4 cm-1,阈值粒子数反转ΔNt=1.6e9 cm-3。
clear;
gt=2.2e-2;
Nt=1.6e15;
N_init=20e15;
Phi_init=1e12;
y=@(t,x)[-2*gt*x(1)/Nt*x(2); 299792458*gt*(x(1)/Nt-1)*x(2)];
[t,x]=ode45(y,[0,5e-6],[N_init,Phi_init]);
[ax,line1,line2]=plotyy(t,x(:,1),t,x(:,2));
ylabel(ax(1),'\Delta\it{N}');
ylabel(ax(2),'\it{\Phi_{\nu}}');
xlabel('\it{t}\rm{/}\it{s}');
ax(1).YColor='r'; line1.Color='r';
ax(2).YColor='b'; line2.Color='b';
[max_Phi,idx]=max(x(:,2));
xlim(ax(1),[0,2*t(idx)]); xlim(ax(2),[0,2*t(idx)]);
ylim(ax(1),[0,1.2*N_init]); ylim(ax(2),[0,1.2*max_Phi]);
set(gca,'FontName','Times New Roman','FontSize',15);
结果如下图所示:
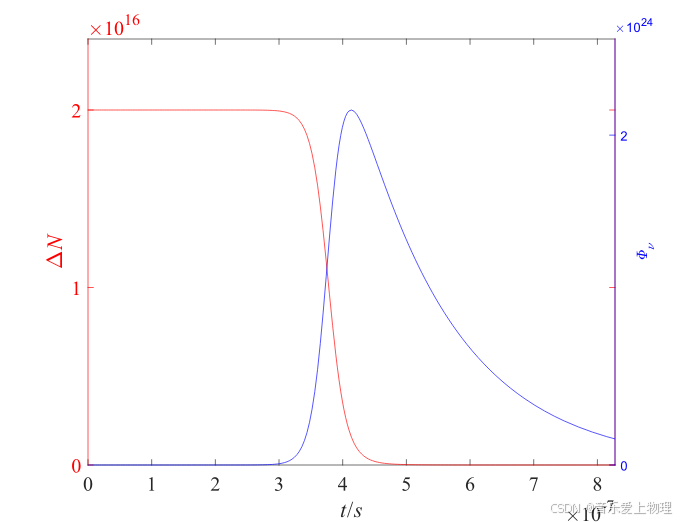




















 1618
1618

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








