（28）语义分割--cross-entropy loss和OhemCELoss

原创已于 2022-10-29 13:29:06 修改 · 928 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#python #人工智能 #机器学习

于 2022-10-28 13:05:08 首次发布

torch 专栏收录该内容

32 篇文章

订阅专栏

本文详细介绍了熵的概念及其在信息论中的应用，接着探讨了Sigmoid函数和二分类交叉熵，包括它们的定义、计算过程和PyTorch中的实现。随后讲解了softmax函数、多分类交叉熵及其在多分类问题中的应用。重点讨论了语义分割中的OhemCELoss损失函数，包括其实现细节和与二分类、多分类交叉熵的关系。

部署运行你感兴趣的模型镜像

1、主要参考

（1）大佬写的很好

https://www.jianshu.com/p/24376b18e5c7

（2）二分类和多分类大佬写的很好

交叉熵损失函数_沙子是沙子的博客-优快云博客_交叉熵损失函数

二分类交叉熵，多分类交叉熵，focal loss_jzdl的博客-优快云博客_二分类交叉熵

（3）二分类的定义和实现

PyTorch学习笔记——二分类交叉熵损失函数 - 知乎

（4）softmax和sigmod的关系见下面，写得很好

Softmax和Sigmoid函数的区别_ciki_tang的博客-优快云博客_softmax和sigmoid

（5）其它概念参考

Sigmoid函数_百度百科

2、什么是熵

参考某度

https://baike.baidu.com/item/%E7%86%B5/19190273?fr=aladdin

信息熵_百度百科

（1）熵 [shāng]，（英语：entropy）。泛指某些物质系统状态的一种量度，某些物质系统状态可能出现的程度。熵的概念是由德国物理学家克劳修斯于1865年提出。1923年，德国科学家普朗克（Planck）来中国讲学用到"entropy"这个词，胡刚复教授翻译时灵机一动，把“商”字加火旁来意译“entropy”这个字，创造了“熵”字（拼音：shāng）。

（2）1948年，香农将统计物理中熵的概念，引申到信道通信的过程中，从而开创了”信息论“这门学科。香农定义的“熵”又被称为“香农熵”或“信息熵”，即

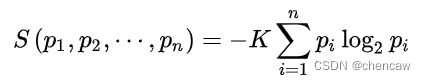
其中 i 标记概率空间中所有可能的样本，pi 表示该样本的出现几率，K是和单位选取相关的任意常数。

(3)上述公式中，如果i有32个取值范围，假设其中，p1，p2 ，　．．．，p32 分别是这 32 个球队夺冠的概率。

S = -(p1*log(2,p1) + p2 * log(2,p2) +　．．．　+p32 *log(2,p32))

注意：当所有样本等几率出现的情况下，熵达到最大值。

3、Sigmoid函数和二分类交叉熵

3.1 sigmoid函数

（1）sigmoid的函数如下图所示

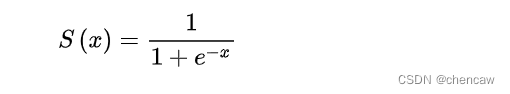
（2）sigmoid函数的作用是将输出压缩于[0, 1]之间

3.2 二分类交叉熵

3.2.1 二分类的交叉熵

（1）假设一个神经网络对应着二分类的输出，注意由于不是0就是1，所以1个神经网络输出。

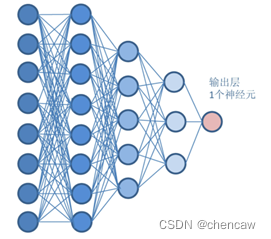
（2）上述网络对应N个样板的输入数据时，对应输出为[X1,X2,…,XN]，该输出取值范围很广，什么数据都有可能。

（3）经过sigmod函数以后，输出的值从[X1,X2,…,XN] 变为 [S1,S2,…,SN]

（4）假设真实的类别为[Y1, Y2,…YN]，注意Yi 不是1就是0，

（5）根据二分类交叉熵函数可以求得第i个输出的交叉熵如下所示：

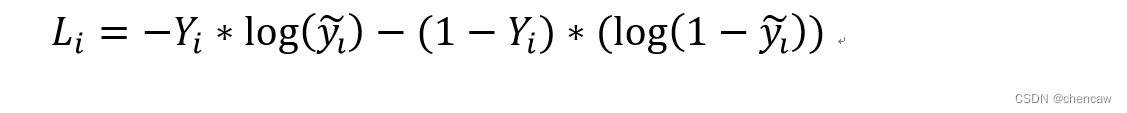
其中：对应上图中的神经网络； 不是1就是0，对应着真实标签； 的取值对应着sigmod函数的输出Si

（6）对所有N个数据的交叉熵求平均，就可得到该组数据的二分类交叉熵函数

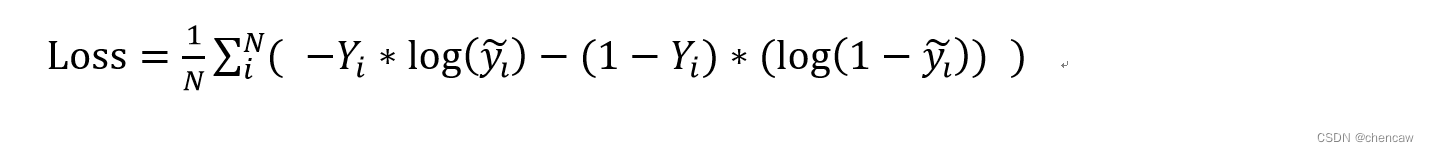
3.2.1 二分类交叉熵的实现过程

参考了

PyTorch学习笔记——二分类交叉熵损失函数 - 知乎

（1）方法1： nn.BCELoss()函数，该函数不自带Sigmoid函数

import torch
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(10, 5),
    nn.Linear(5, 1),
    nn.Sigmoid()
)
criterion = nn.BCELoss()

x = torch.randn(16, 10)  # (16, 10)
y = torch.empty(16).random_(2)  # shape=(16, ) 其中每个元素值为0或1

out = model(x)  # (16, 1)
out = out.squeeze(dim=-1)  # (16, )

loss = criterion(out, y)
print(loss.item())

（2）方法二：nn.BCEWithLogitsLoss函数，该函数自带了Sigmoid函数

import torch
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(10, 5),
    nn.Linear(5, 1),
)
criterion = nn.BCEWithLogitsLoss()

x = torch.randn(16, 10)  # (16, 10)
y = torch.empty(16).random_(2)  # shape=(16, ) 其中每个元素值为0或1

out = model(x)  # (16, 1)
out = out.squeeze(dim=-1)  # (16, )

loss = criterion(out, y)
print(loss.item())

4、softmax和多分类交叉熵

4.1多分类输出的神经网络

（1）比如：某神经网络的输出为3个分类，对应(狗，猫，鱼)，简单的网络结构如下图所示

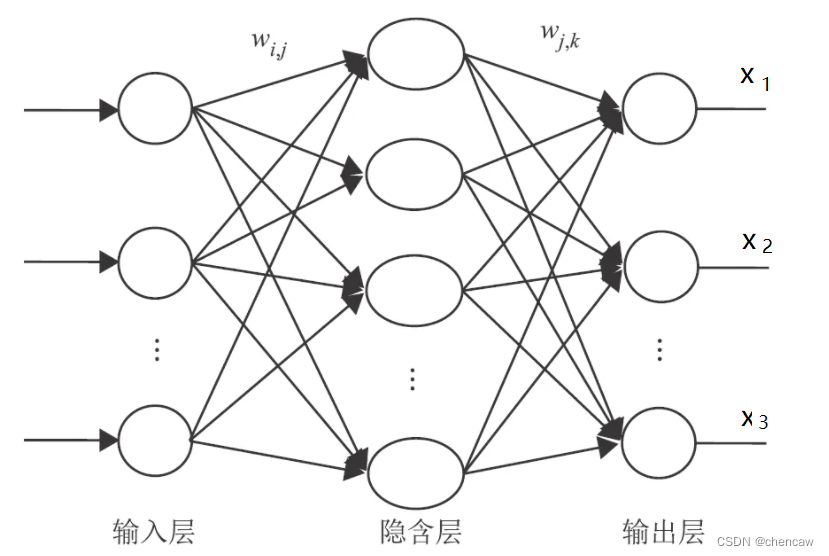
（2）神经网络的输出可能是怪怪的，什么数据都有；假设有2张图片输入，对应的神经网络输出如下：

类别（狗，猫，鱼）对应分类标签（0,1,2）
1) 假设第一张图片是类别猫，对应的输出为[-2, 0.6 ,1]；
2) 假设第二张图片是类别狗，对应的输出为[0.5, 1.2 ,-1.5]；

（3）这个时候怎么求他们的概率呢？

4.2 sofmax函数

softmax函数，又称归一化指数函数。它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。

（1）其公式定义为：

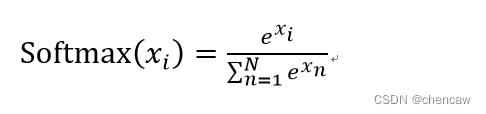
（2）原理：

1）通过自然对数换算所有的输出（PS：这样就没有负数了）；
2）所有换算过的输出累加；
3）每个输出/所有输出的和，换算成0--1之间分布的概率；
4）而后所有输出概率的概率和为1。

4.3 多分类交叉熵损失函数

（1）每一个具体类别物体的交叉熵。给定两个概率分布p和q，通过q来表示p的交叉熵为

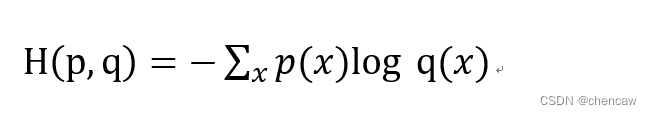
交叉熵刻画的是两个概率分布之间的距离， p代表正确答案， q代表的是预测值，交叉熵越小，两个概率的分布约接近。

（2）多分类总共交叉熵函数的定义如下（PS：没什么就是上面每个分类的交叉熵求一下和）：

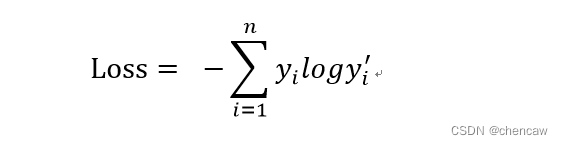
其中： 𝒚𝒊为标签值， 𝑦𝑖′ 为预值测

𝑦𝑖′ 就是softmax的输出

（2）独热编码

备注：类别（狗，猫，鱼）对应分类标签（0,1,2）；

𝒚𝒊标签取值注意：

狗的时候对应独热编码[1 0 0];

猫的时候对应独热编码[0 1 0];

鱼的时候对应独热编码[0 0 1]

4.4 对应上面神经网络图的计算交叉熵例子

（1）有2张图片输入，对应的神经网络输出如下：

类别（狗，猫，鱼）对应分类标签（0,1,2），对应独热编码[1 0 0]、[0 1 0]和[0 0 1]
1) 假设第一张图片是类别猫，对应的输出为[-2, 0.6 ,1]；
2) 假设第二张图片是类别狗，对应的输出为[0.5, 1.2 ,-1.5]；

（2）经过softmax计算后数值为(测试代码chenlosstest2.py)：

import torch
import torch.nn as nn

#输出类别（狗，猫，鱼）对应分类标签（0,1,2）
output = torch.FloatTensor([[-2, 0.6, 1],[0.5, 1.2, -1.5]])
Softmax = nn.Softmax(dim=1) #沿dim的每个切片和为1
s_output = Softmax(output)
print(s_output)

输出数值为：

tensor([[0.0289, 0.3897, 0.5814],
[0.3176, 0.6395, 0.0430]])

（3）具体每一个类的交叉熵计算过程如下：

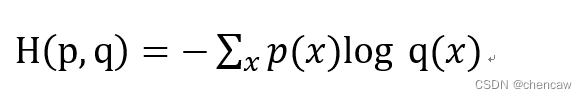
第一张图片是猫，所以L1：

L1 = H( (0,1,0),(0.0289, 0.3897, 0.5814) ) = -log(0.3897) = 0.9424

第二张图片是狗，所以L2：

L2 = H( (1,0,0),(0.3176, 0.6395, 0.0430) ) = -log(0.3176) = 1.1470

（4）所以多分类的整体交叉熵损失为：

Loss = L1 + L2 = 2.0894‬

（5）测试代码实现chenlosstest3.py，

方法一，使用函数NLLLoss函数，该函数不自带softmax和log功能

方法二，使用函数CrossEntropyLoss函数，该函数自带了softmax和log功能

import torch
import torch.nn as nn

#输出类别（狗，猫，鱼）对应分类标签（0,1,2）
output = torch.FloatTensor([[-2, 0.6, 1],[0.5, 1.2, -1.5]])
# Softmax = nn.Softmax(dim=1) #沿dim的每个切片和为1
# s_output = Softmax(output)
# print(s_output)

#target是真实的标签纸，这里对应类别（狗，猫，鱼）对应分类标签（0,1,2）
#至于独热编码计算，函数会搞定的
target = torch.tensor([1,0])

#方法一
NLLLoss = nn.NLLLoss()  #不带softmax和log
NLL_out = torch.log(torch.softmax(output, dim=-1))
loss_NLL_output = NLLLoss(NLL_out,target)
print("方法一： ",loss_NLL_output)

#方法二
loss_function = nn.CrossEntropyLoss()    #自带softmax和log
loss_cross_output = loss_function(output,target)
print("方法二： ",loss_cross_output)


# nllloss = nn.NLLLoss()
# predict = torch.Tensor([[2, 3, 1],
#                         [3, 7, 9]])
# predict = torch.log(torch.softmax(predict, dim=-1))
# label = torch.tensor([1, 2])
# nllloss_out = nllloss(predict, label)
# print(nllloss_out)

# cross_loss = nn.CrossEntropyLoss()

# predict = torch.Tensor([[2, 3, 1],
#                         [3, 7, 9]])
# label = torch.tensor([1, 2])
# cross_loss_out = cross_loss(predict, label)
# print(cross_loss_out)
# # output: tensor(0.2684)

tensor(1.0447)

注意：nn.CrossEntropyLoss计算的是model输出结果中多个样本的loss均值

也就是求了 .mean()

4、多分类和二分类的关系

二分类可以理解为多分类在n=2时候的特殊例子，标签不是0就是1，两个对象的概率和为1。

5、语义分割OhemCELoss 损失函数的实现

主要参考里的大佬真的讲的很细了，再应用一遍

https://www.jianshu.com/p/24376b18e5c7

bisenet中使用的 OhemCELoss比大佬的代码简单些，n_min参数由计算获得

5.1 OhemCELoss 的代码实现

（1）代码定义

class OhemCELoss(nn.Module):

    def __init__(self, thresh, lb_ignore=255):
        super(OhemCELoss, self).__init__()
        self.thresh = -torch.log(torch.tensor(thresh, requires_grad=False, dtype=torch.float)).cuda()
        # self.thresh = -torch.log(torch.tensor(thresh, requires_grad=False, dtype=torch.float))
        self.lb_ignore = lb_ignore
        self.criteria = nn.CrossEntropyLoss(ignore_index=lb_ignore, reduction='none')

    def forward(self, logits, labels):
        n_min = labels[labels != self.lb_ignore].numel() // 16
        loss = self.criteria(logits, labels).view(-1)
        loss_hard = loss[loss > self.thresh]
        if loss_hard.numel() < n_min:
            loss_hard, _ = loss.topk(n_min)
        return torch.mean(loss_hard)

（2）调用的例子

criteria_pre = OhemCELoss(0.7, lb_ignore)

5.2 具体细节

（1）定义了阈值

self.thresh = -torch.log(torch.tensor(thresh, requires_grad=False, dtype=torch.float)).cuda()

（1）其中 thresh 表示的是，损失函数大于多少的时候，会被用来做反向传播。需要注意一点，参数 thresh 是概率，即小于这个概率的预测值会参与计算损失。

（2）log操作将概率转化为其对应的 loss 。

（2）计算获得n_min参数值，像素点的个数整除16向下取整。

python中“//”是一个算术运算符，表示整数除法，它可以返回商的整数部分（向下取整）。

numel()函数：返回数组中元素的个数

n_min = labels[labels != self.lb_ignore].numel() // 16

n_min 表示的是，在一个 batch 中，最少需要考虑多少个样本。

（3）交叉熵函数的定义

self.criteria = nn.CrossEntropyLoss(ignore_index=lb_ignore, reduction='none')

（1）代码中的 logits 维度为 [N, C, H, W]，labels 维度为[N, H, W] 。上面的函数设置 reduction 为 none，保留每个元素的损失，返回的维度为N,H,W

（2）C维度的丢失，看多分类交叉熵的计算过程，相当于多个输出对应某标签

（4）逐个元素计算交叉熵损失

loss = self.criteria(logits, labels).view(-1)

将预测的损失拉平为一个长向量，每个元素为一个 pixel 的损失。

（5）将长向量中每个 pixel 的损失按从大到小排序

loss = self.criteria(logits, labels).view(-1)

（6）获取实际计算所得的所有大于该阈值的元素的交叉熵损失值

loss_hard = loss[loss > self.thresh]

（7）如果上式得到个数不够

if loss_hard.numel() < n_min:

因为我们最少也要考虑 n_min 个损失最大的 pixel

        if loss_hard.numel() < n_min:
            loss_hard, _ = loss.topk(n_min)

您可能感兴趣的与本文相关的镜像

PyTorch 2.5

PyTorch

Cuda

PyTorch 是一个开源的 Python 机器学习库，基于 Torch 库，底层由 C++ 实现，应用于人工智能领域，如计算机视觉和自然语言处理