【MATLAB例程】二维状态量的UKF例程，用于非线性滤波，简化版例程，用于普适性的非线性状态估计。附代码下载链接

二维状态量的UKF例程，MATLAB，用于非线性滤波，简化版例程，用于普适性的非线性状态估计，状态量和观测量都是非线性的，便于调试和修改。有中文注释

程序概述

这段代码实现了一个简化版的二位状态量的无迹卡尔曼滤波（$UKF$）的例程，主要用于给出一个普适性的二维滤波框架，便于后期修改为自己需要的滤波结构

核心功能

1. 模型初始化：设置时间序列、过程噪声和观测噪声的协方差矩阵，并初始化状态向量和观测值。
2. 运动模型：通过迭代过程生成真实状态和未滤波状态，同时计算观测值。
3. UKF 处理：
   • 生成 sigma 点和权重。
   • 预测下一状态和协方差矩阵。
   • 进行观测更新，校正状态估计。
4. 结果可视化：绘制真实状态、滤波后的状态、误差比较以及误差的累计概率分布图。

测试结果

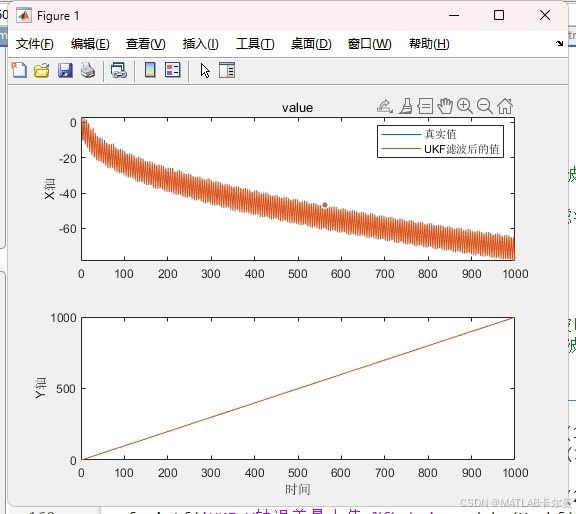
各维度状态量的曲线：

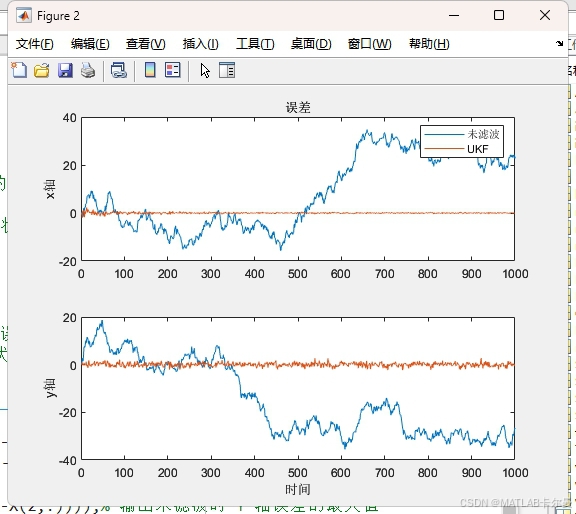
各维度的状态量误差曲线：

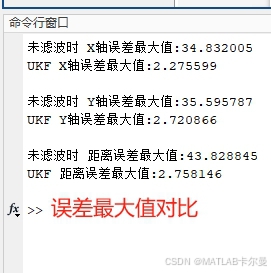
误差最大值对比：

MATLAB源代码

完整代码如下：

% 二维状态量的UKF例程，简化版的例程（没有严格的组合导航推导）
% 作者：matlabfilter
% 2025-08-24/Ver1
clear;clc;close all; %清空工作区、命令行，关闭小窗口
rng(0); %固定随机种子

%% 滤波模型初始化
% 定义时间序列
t = 1:1:1000;
% 过程噪声协方差矩阵和过程噪声
Q = 1*diag([1,1]);
w = sqrt(Q)*randn(size(Q,1),length(t));
% 观测噪声协方差矩阵和观测噪声
R = 1*diag([1,1]);
v = sqrt(R)*randn(size(R,1),length(t));
% 初始状态估计协方差矩阵
P0 = 1*eye(2);
% 初始化状态向量
X = zeros(2,length(t));
% 初始化扩展卡尔曼滤波状态向量
X_ukf = zeros(2,length(t));
X_ukf(:,1) = X(:,1); %给滤波后的状态量赋初值
Z = zeros(2,length(t));% 给观测值分配空间
Z(:,1) = [X(1,1)^2/20;X(2,1)] + v(:,1);% 定义初始观测值

%% 运动模型
% 初始化未滤波的状态向量
X_ = zeros(2,length(t)); %给未滤波的值分配空间
X_(:,1) = X(:,1); %给未滤波的值赋初值
% 运动模型迭代
for i1 = 2:length(t)
    % 计算真实状态值
    X(:,i1) = [X(1,i1-1) + (2.5 * X(1,i1-1) / (1 + X(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
        X(2,i1-1) + 1];
    % 计算未滤波的状态值
    X_(:,i1) = [X_(1,i1-1) + (2.5 * X_(1,i1-1) / (1 + X_(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
        X_(2,i1-1) + 1] + w(:,i1-1);
    % 计算观测值
    Z(:,i1) = [X(1,i1).^2 / 20;X(2,i1)] + v(i1);
end

%% UKF部分

完整代码的下载链接：
https://download.youkuaiyun.com/download/callmeup/91746518

或：