【matlab技巧】绘制PDF（概率密度函数）图像——以均匀分布、高斯分布、双高斯分布为例

在 MATLAB 中，可以使用 histogram 函数绘制噪声序列的概率密度函数 (PDF) 图像。
以下是一个示例，展示如何生成噪声序列并绘制其 PDF。

源代码

% 绘制PDF（概率密度函数）图像——以均匀分布、高斯分布、双高斯分布为例
% 2025-06-11/Ver1
% 作者：matlabfilter

clc;clear;close all;
% 生成噪声序列
n = 10000; % 噪声样本数量
%% 均匀分布
noise1 = rand(n, 1); % 生成均匀分布噪声

% 绘制概率密度函数 (PDF)
figure;
histogram(noise1, 'Normalization', 'pdf'); % 归一化为概率密度
hold on;

% 绘制标准均匀分布的理论 PDF
x = linspace(-4, 4, 100);
pdf_uniform = zeros(size(x)); % 预先分配空间
pdf_uniform(x >= 0 & x <= 1) = 1; % 在[a,b]区间内为常数

plot(x, pdf_uniform, 'r', 'LineWidth', 2); % 绘制理论 PDF
% pdf = normpdf(x, 0, 1); % 理论 PDF
% plot(x, pdf, 'r', 'LineWidth', 2); % 绘制理论 PDF

% 设置图形属性
title('均匀分布——噪声序列的概率密度函数 (PDF)');
xlabel('值');
ylabel('概率密度');
legend('样本 PDF', '理论 PDF');
%% 高斯分布
noise2 = randn(n, 1); % 生成标准正态分布噪声

% 绘制概率密度函数 (PDF)
figure;
histogram(noise2, 'Normalization', 'pdf'); % 归一化为概率密度
hold on;

% 绘制标准正态分布的理论 PDF
x = linspace(-4, 4, 100);
pdf = normpdf(x, 0, 1); % 理论 PDF
plot(x, pdf, 'r', 'LineWidth', 2); % 绘制理论 PDF

% 设置图形属性
title('高斯分布——噪声序列的概率密度函数 (PDF)');
xlabel('值');
ylabel('概率密度');
legend('样本 PDF', '理论 PDF');

%% 双高斯分布
p1 = 0.3;
p2 = 1 - p1; % 第二高斯分布的概率
% noise3= zeros(N, m);
for i1 = 1:n % 生成双高斯噪声
    if rand < p1
        noise3(i1,:) = normrnd(0, 1);
    else
        noise3(i1,:) = normrnd(20, 10);
    end
end
% noise = randn(n, 1); % 生成标准正态分布噪声

% 绘制概率密度函数 (PDF)
figure;
histogram(noise3, 'Normalization', 'pdf'); % 归一化为概率密度
hold on;

% 绘制标准正态分布的理论 PDF
x = linspace(-30, 70, 1000);
pdf = p1*normpdf(x, 0, 1) + p2*normpdf(x, 20, 10); % 理论 PDF
plot(x, pdf, 'r', 'LineWidth', 2); % 绘制理论 PDF

% 设置图形属性
title('高斯分布——噪声序列的概率密度函数 (PDF)');
xlabel('值');
ylabel('概率密度');
legend('样本 PDF', '理论 PDF');

运行结果

得到的三种分布示例如下：

均匀分布

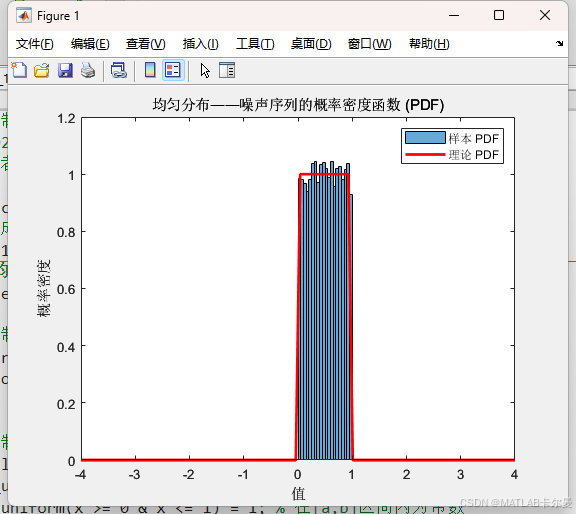
高斯分布

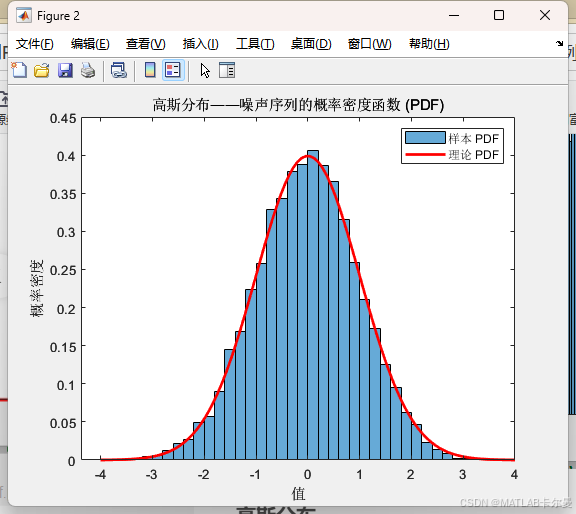
双高斯分布为例

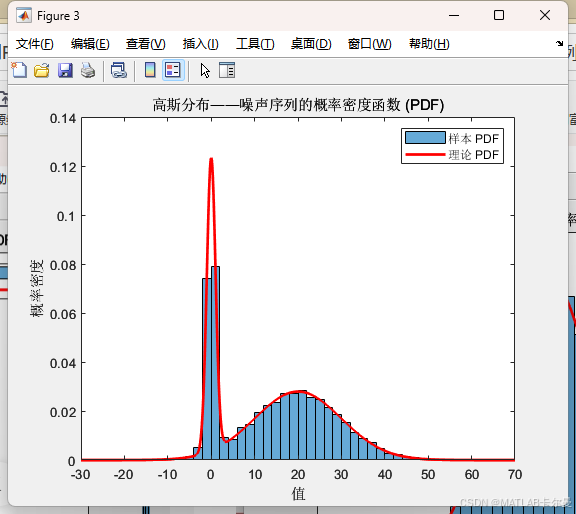
代码说明

1. 生成噪声序列：

   • 使用 randn 函数生成噪声序列。

2. 绘制 PDF：

   • 使用 histogram 函数绘制噪声序列的直方图，并通过 'Normalization', 'pdf' 选项将其归一化为概率密度。

3. 绘制理论 PDF：

   • 计算理论 PDF，并使用 plot 函数绘制。

4. 设置图形属性：

   • 添加标题、标签和图例，使用 grid 进行网格设置。

相关公式

以下是三种分布的理论公式，基于您提供的MATLAB代码参数推导得出：

1. 均匀分布（Uniform Distribution）

参数范围：$a=0$, $b=1$
概率密度函数（PDF）：
$$f_{\text{uniform}}(x)=\{\begin{array}{ll}1& \text{for }0\le x\le 1\\ 0& \text{otherwise}\end{array}$$

2. 高斯分布（Gaussian Distribution）

参数：均值 ( \mu = 0 )，标准差 ( \sigma = 1 )
概率密度函数（PDF）：
$$f_{\text{gaussian}}(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$$

3. 双高斯混合分布（Gaussian Mixture Distribution）

参数设定：

• 分量1：均值 ( \mu_1 = 0 )，标准差 ( \sigma_1 = 1 )，权重 ( p_1 = 0.3 )
• 分量2：均值 ( \mu_2 = 20 )，标准差 ( \sigma_2 = 10 )，权重 ( p_2 = 0.7 )

概率密度函数（PDF）：
$$f_{\text{mixture}}(x)=p_1\cdot f_1(x)+p_2\cdot f_2(x)$$
其中：
$$f_1(x)=\frac{1}{\sqrt{2\pi }{\sigma }_1}{e}^{-\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}}=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$$
$$f_2(x)=\frac{1}{\sqrt{2\pi }{\sigma }_2}{e}^{-\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2}}=\frac{1}{10\sqrt{2\pi }}{e}^{-\frac{(x-20{)}^2}{200}}$$

分布特性对比表

特性	均匀分布	高斯分布	双高斯混合分布
支撑集	([0, 1])	((-\infty, +\infty))	((-\infty, +\infty))
峰值位置	无峰值（常数）	(x=0)	(x=0) 和 (x=20)
峰值高度	1.0	(\approx 0.4)	(\approx 0.4) 和 (\approx 0.04)
方差	(\frac{(1-0)^2}{12} \approx 0.083)	(1)	(0.3 \times 1 + 0.7 \times 100 = 70.3)
偏度	(0)	(0)	正偏（右侧分布主导）

另有

另有绘制CDF（累计概率密度函数）的文章：

• 累积分布函数图（CDF）的介绍、matlab的CDF图绘制方法（附源代码）：https://blog.youkuaiyun.com/callmeup/article/details/137754111?spm=1011.2415.3001.5331

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者