Sage husa下的自适应粒子滤波（PF）代码

该 MATLAB 代码旨在比较传统粒子滤波（$PF$）与自适应粒子滤波（$APF$）的效果，特别是在三维状态跟踪的场景下。通过引入$Sage-Husa$算法，该代码实现了对观测噪声的自适应调整，以提高滤波器的性能。

介绍：Sage Husa自适应的APF三维滤波效果对比

该 MATLAB 代码旨在比较传统粒子滤波（PF）与自适应粒子滤波（APF）的效果，特别是在三维状态跟踪的场景下。通过引入Sage-Husa算法，该代码实现了对观测噪声的自适应调整，以提高滤波器的性能。

主要功能

1. 参数初始化：

   • 设置粒子总数、时间向量、过程噪声和观测噪声的协方差矩阵，并生成相应的噪声。
   • 初始化真实状态和观测值矩阵。

2. 真实状态生成：

   • 使用非线性动态模型更新真实状态，并计算相应的观测值。

3. 粒子滤波（PF）算法：

   • 预测步骤：对每个粒子进行状态预测，并计算基于当前观测的权重。
   • 归一化权重：对所有粒子的权重进行归一化处理。
   • 重采样步骤：根据权重重采样粒子，更新粒子集合。

4. 自适应粒子滤波（APF）算法：

   • 在粒子滤波的基础上，采用Sage-Husa算法动态更新观测噪声协方差，以适应不同状态下的观测噪声特性。

5. 结果可视化：

   • 绘制真实状态与滤波后的状态估计，以及对应的误差。
   • 通过累积分布函数（CDF）比较不同滤波方法的误差分布。

6. 性能评估：

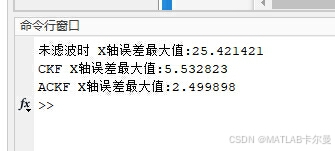
   • 输出未滤波、PF和APF在第一维状态量上的最大和平均误差，为算法的效果提供定量评价。

该代码为研究和应用粒子滤波及其自适应变体提供了一个有效的工具，适合在动态系统中的状态估计和跟踪任务。

MATLAB代码

部分代码如下：

% Sage Husa自适应的APF三维滤波效果对比
% 2024-12-23/Ver1
clear; clc; close all; % 清空工作空间、命令窗口和关闭所有图形窗口
rng(0); % 设置随机数生成器的种子，确保结果可复现
%% 参数设置
N = 100; % 粒子总数
t = 1:1:1000; % 时间向量，从1到1000
Q = 1*diag([1,1,1]); % 过程噪声的协方差矩阵
w_pf = sqrt(Q) * randn(size(Q,1), length(t)); % 生成过程噪声，维度与状态一致
R = 1*diag([1,1,1]); % 观测噪声的协方差矩阵
v_pf = sqrt(10*R) * randn(size(10*R,1), length(t)); % 生成观测噪声，维度与观测一致
P0 = 1 * eye(3); % 初始状态的协方差矩阵
X = zeros(3, length(t)); % 初始化真实状态矩阵
Z = zeros(3, length(t)); % 定义观测值矩阵
Z(:, 1) = [X(1, 1)^2 / 20; X(2, 1); X(3, 1)] + v_pf(:, 1); % 计算初始观测值

% 设定变量维度
X_ = zeros(3, length(t)); % 初始化未滤波状态矩阵
X_(:, 1) = X(:, 1); % 设置初始未滤波状态
w = zeros(3, N); % 初始化权重矩阵

for i1 = 2:length(t) % 遍历时间步
    % 生成真实状态

end

%% 初始化粒子群
for i1 = 1:N % 对每个粒子进行初始化

end
X_pf(:, 1) = sum(P, 2) / N; % 计算初始时刻所有粒子的几何中心位置
X_apf(:, 1) = sum(P, 2) / N; % 计算初始时刻所有粒子的几何中心位置

%% 粒子滤波PF
for k = 2:length(t) % 遍历每个时间步
    % 粒子滤波
    % 预测步骤
    for i = 1:N % 对每个粒子进行预测
        % 更新粒子位置

运行结果

状态曲线：

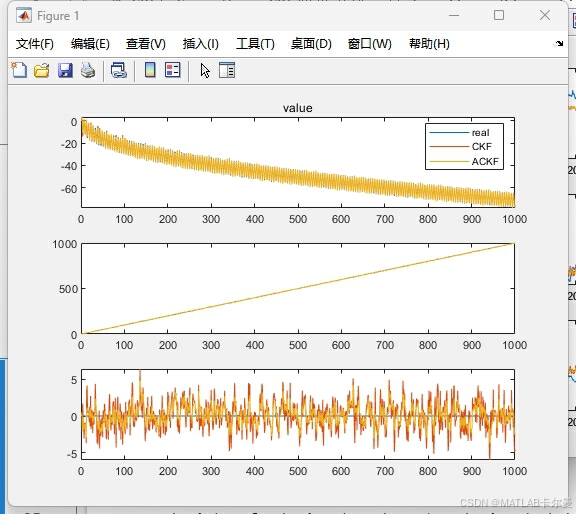
误差曲线：

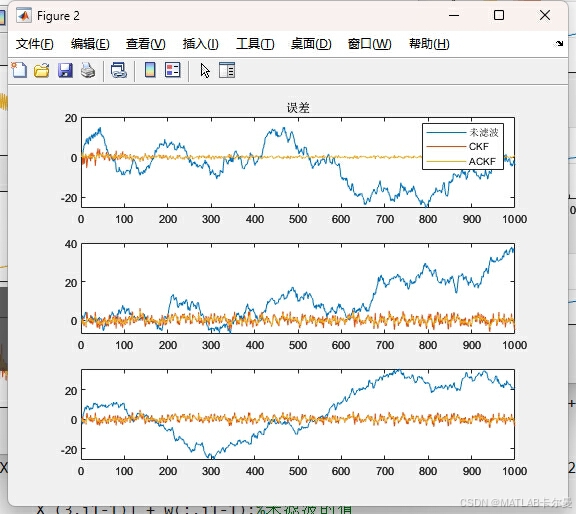
误差统计特性：

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击文末卡片联系作者