基于高阶平滑的加密音频可逆数据隐藏

基于高阶平滑的加密音频可逆数据隐藏

摘要

本文提出了一种针对加密音频文件的可逆数据隐藏方法，其中数据隐藏者在不了解原始内容的情况下，尝试将一些附加数据嵌入到由内容所有者分发的加密内容中。合法接收者使用预先协商的解密密钥可以解密加密内容，并获得与原始介质几乎相同的版本。此外，如果他/她还拥有预先协商的数据隐藏密钥，则可以提取嵌入的数据，从而完全恢复原始介质。目前存在多种媒体类型，近年来已有一些研究致力于在加密图像中隐藏数据。由于人类听觉系统比人类视觉系统更为敏感，本文采用高阶平滑度测量来保持声音的自然性，并让内容所有者在加密前预先计算声音恢复所需的关键信息。通过这两种机制，本方法生成的隐写音频质量退化较小，并能够以零误码率完全恢复原始音频。

关键词

可逆数据隐藏 · 加密音频 · 高阶平滑度

1 引言

数据隐藏技术在过去几十年中得到了广泛研究。它为多媒体增加了附加数据，可用于元数据记录、认证和隐蔽通信等用途。其中，可逆数据隐藏旨在提取附加数据后能够完全恢复宿主媒体，在生物识别系统或军事通信中具有良好的适用性，因为在这些应用场景中不允许对媒体进行任何失真或修改。数据可逆性的概念最早由Barton在1997年的专利中提出[1]。

鉴于可逆性是必须的，在设计一种优秀的可逆数据隐藏方法时还有四个额外目标：
- 不可感知性，或隐写信号质量的轻微下降。
- 高容量，或大嵌入载荷。
- 不可检测性，或良好的隐写数据隐蔽性。
- 效率，或较小的计算负载。

良好的设计原则可以在四个目标中的两个之间实现权衡。例如，较大的嵌入载荷显然会导致更大的质量退化，或者一种兼具高容量和小质量退化的良好设计方法通常需要更多的计算时间。

大多数现有的可逆数据隐藏方法都是在明文域中实现的，可以分为三类。第一类位于空间域。该领域的工作通常具有简单直接和高效率的优点。其中大部分又可进一步分为基于差值扩展的方法[2–4]（[4]用于音频）和基于直方图修改的方法[5–7]（[7]用于音频）。第二类位于频谱域。在[8]，Huang通过将原始音频转换到整数DCT（intDCT）域，在高频部分创建了一个嵌入空间，以隐藏额外的有效载荷数据。第三类位于压缩域。在[9]，Li利用编码比特流的一些特性，将有效载荷数据嵌入到压缩语音中。

总体而言，在明文域中，可以充分利用给定媒体的自然特性进行数据隐藏。但随着当今对隐私需求的不断增长，数据在分发或处理之前很可能会被加密。因此，最近提出了一些在密文域中设计和实现的隐藏方法[10–12]。在[10]，Zhang提出了一种新的草图方案，在该方案下设计了一种有效的方法，将附加数据嵌入到异或加密图像中。他首先将加密图像分割为非重叠块，然后对于每个块，分别通过翻转组A或组B中所有加密像素的3个最低有效位来嵌入一位‘0’或‘1’。组A和组B是互斥的，并由数据隐藏密钥确定。由于该工作基于对称加密系统构建，Zhang的工作保持了与在空间域中完成的工作相同的效率优势。在本文中，我们处理的是加密音频，并提出了一种改进方案以及一种具有不可感知性、效率和可接受容量的可逆数据隐藏方法。

人类听觉系统比人类视觉系统更敏感，因此即使对音频信号进行轻微修改也容易被察觉[7]。为了减小隐写音频质量的下降，我们为每个音频段/帧计算一种平滑度阈值，定义为NBI（翻转比特数）。显然，在一个音频帧中翻转更多样本的最低有效位会使该帧变得更不平滑，因此NBI被定义为满足修改后的音频帧比原始帧更不平滑的最小值。通过更优的平滑度度量，NBI可以更小，从而更好地适用于我们在音频上的数据隐藏工作。

在[10]，张定义了
$$
h = \sum_{u=2}^{s-1} \sum_{v=2}^{s-1} \left| p_{u,v} - \frac{p_{u-1,v} + p_{u,v-1} + p_{u+1,v} + p_{u,v+1}}{4} \right|,
$$
作为测试图像块中像素空间相关性的度量函数，其中 $ p_{u,v} $ 表示位于位置 $(u, v)$ 的像素值，$ s $ 表示块大小。较低的 $ h $ 函数值意味着更高的相关性和局部平滑性。

式(1)的一维版本可写为
$$
\tilde{h} = \sum_{l=2}^{f-1} \left| S_l - \frac{S_{l-1} + S_{l+1}}{2} \right|,
$$
其中 $ S_l $ 表示音频帧中第 $ l $ 个样本的值，$ f $ 表示帧大小。公式(1)和(2)均为二阶平滑度测量函数，当目标媒体为音频时，它们的性能已不再足够理想。因此，在本方案中考虑了 $ \tilde{h} $（或 $ h $）的高阶版本，实验结果表明，在公开可用的RWC音乐数据库上，隐写音频的质量下降可以忽略不计[15]。

2 方案与算法

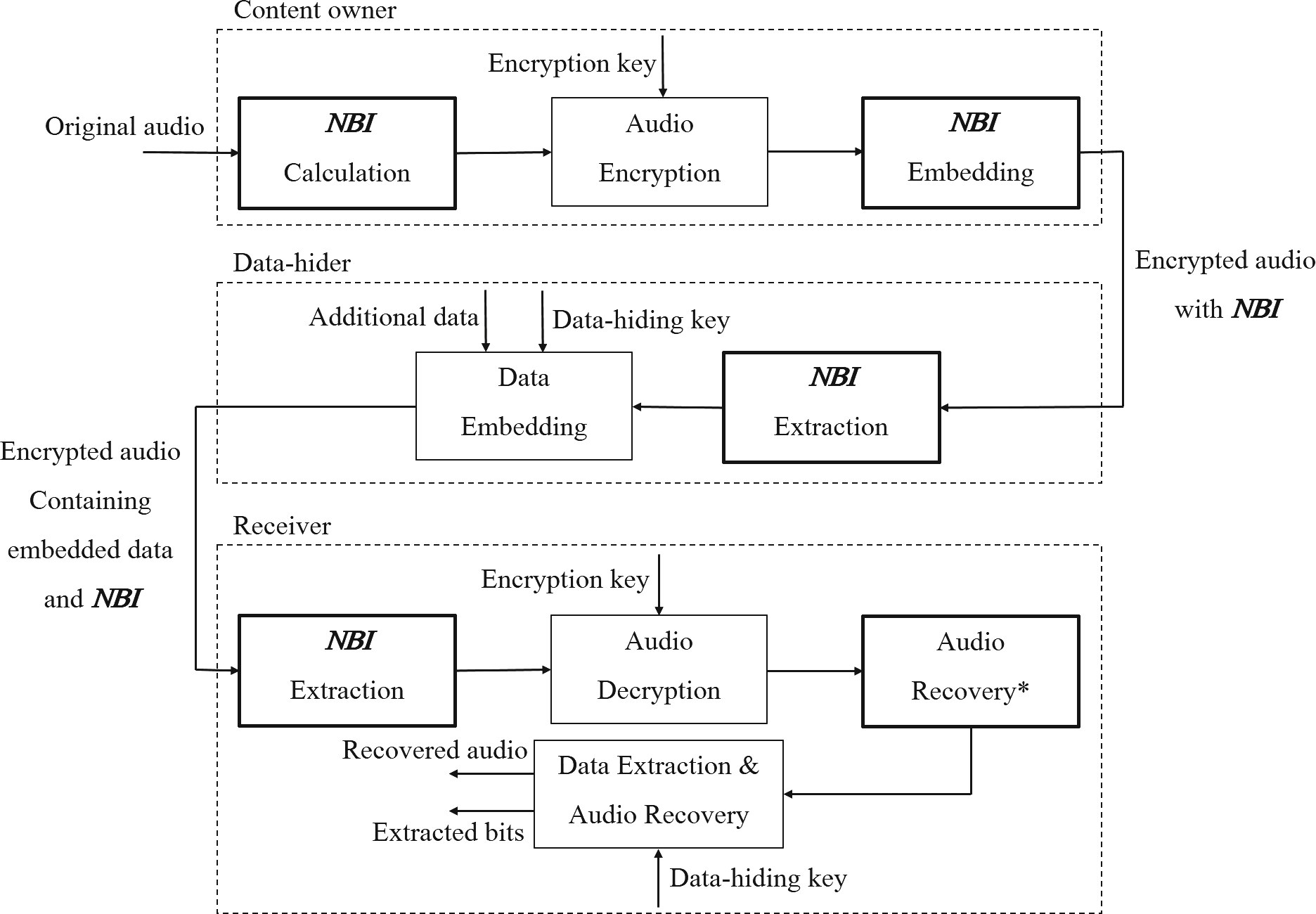
张[10]提出的方案的一个修改版本，其中（1）NBI信息从内容所有者传输到数据隐藏者，再传输到接收者，（2）提出了一些新的子过程，以及（3）目标媒体从图像更改为音频。

沿用类似的思想，内容所有者使用加密密钥对原始音频进行加密，然后数据隐藏者在不了解内容的情况下，基于数据隐藏密钥将一些附加数据嵌入到加密音频中。如果接收者拥有预先协商的加密/解密密钥，则他/她可以首先解密加密音频，得到一个高质量的嵌入数据但已解密的版本，其听感与原始音频非常相似。通过预先协商的数据隐藏密钥，他/她还可以进一步恢复原始音频并提取出嵌入的附加数据。本方案与[10]的主要区别在于，NBI信息由数据所有者预先计算，然后数据隐藏者借助该信息进行数据嵌入，从而获得显著更好的性能。这一改进的动机在于，人类听觉系统比视觉系统更为敏感[7]，因此在关注感知质量时，音频通常要求比图像更高的SNR（信噪比）值。注意，在图1中，边框较粗的功能模块是新提出的具体子过程，并采用星号符号来区分名称相似但功能不同的功能模块。

在接下来的大多数讨论中，给定的音频被分割成不重叠的帧，且每个帧由 $ f $ 个样本组成。也就是说，原始音频可以表示为一系列音频帧 $ F_k $，其中
$$
F_k = [S_{k,0}, S_{k,1}, …, S_{k,f-1}], \quad k = 0, 1, 2, …
$$
在公式(3)中，$ S_{k,l} $（$ 0 \leq l \leq f - 1 $）表示音频第 $ k $ 帧的第 $ l $ 个样本，其可以用二进制形式表示为
$$
S_{k,l} = \sum_{u=0}^{t-1} b_{k,l,u} \cdot 2^u.
$$
如果使用 $ t $ 位量化器对每个音频样本进行量化。换句话说，如果 $ t = 16 $，一个音频样本值将位于[-32768, 32767]范围内。

2.1 内容所有者端

如图1所示，内容所有者的工作可分为以下三个步骤。

NBI计算

在此步骤中，内容所有者预先计算NBI信息，该信息将由数据隐藏者用于数据隐藏。对于每一帧 $ F_k $，通过算法NBIk确定一个介于1和$ t $之间的整数，该过程由算法1实现。

函数 $ g $ 用于衡量音频的平滑度和/或自然度。直观上，自然音频中两个连续样本之间的差异是有限的，因此公式(2)是$ g $的一个候选，可进一步写成功能形式为
$$
h(A) = \frac{1}{2} \text{sum}(\text{abs}(d(d(A)))),
$$
其中 $ A $ 是一个输入音频帧（例如 $ A = F_k $）或一个音频样本数组，abs和sum分别表示求和和绝对值运算符，且
$$
d(A \equiv [S_1, S_2, S_3, …, S_n]) \equiv [S_2 - S_1, S_3 - S_2, …, S_n - S_{n-1}].
$$
此外，我们定义
$$
d^{(2)}(A) = d(d(A)), \quad d^{(n)}(A) = d(d^{(n-1)}(A)), \quad n = 3, 4, 5, …
$$
从公式5中省略标量1/2后，最终 $ g $ 可表示为
$$
g(A) = \text{sum}(\text{abs}(d^{(2)}(A))).
$$
的值 $ g(F_K) $ 随着 $ F_k $ 变得更加平滑而变小。有关 $ g $ 函数选择的更多讨论，请参见第3.2节以了解详细信息。

简而言之，算法1中的步骤5到步骤11对所有 $ F_k $ 的样本的最低有效位进行了反转。图2展示了对该操作在正弦波上执行的结果，从图2中可以明显看出，随着 $ m $ 的值增大，输出波形的波动也随之变大。对于给定函数 $ g $，计算出具有可能最小值的NBIk可帮助数据隐藏者以非常好的性能进行嵌入工作，即在生成的隐写音频中实现非常小的质量下降。

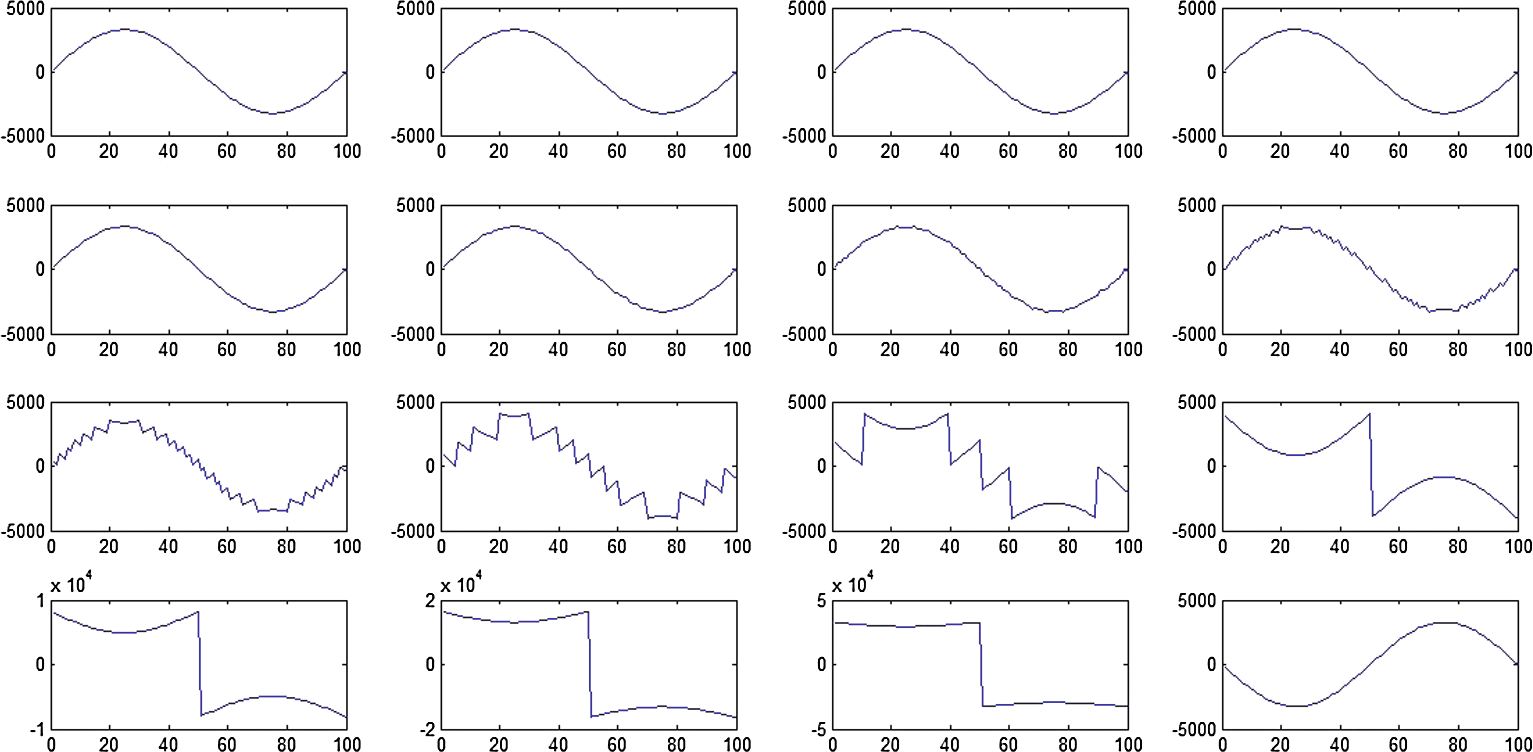
对正弦波的16位100个样本的所有最低有效位进行反转 $ m $（$ 1 \leq m \leq 16 $）后的结果波形。$ m $ 按照扫描线顺序（即从左到右、从上到下）从1变化到16。

如图1所示，必须产生额外的通信开销，以将NBI信息/序列从数据所有者端传输到数据隐藏者端，且该开销与帧大小成反比，因为当帧大小减小时，需要传输的NBI数量增加。然而，可以将NBIk的比特嵌入到加密音频帧 $ F_k $ 中，以消除该开销（详见第2.1节）。

音频加密

为了保持密文的大小与明文相同，采用标准流密码对目标音频进行加密。密文音频样本的相应比特位 $ B_{k,l,u} $ 由以下方式确定
$$
B_{k,l,u} = b_{k,l,u} \otimes r_{k,l,u}, \quad 0 \leq l \leq f - 1, \quad 0 \leq u \leq t - 1,
$$
其中 $ r_{k,l,u} $ 是加密密钥，“$\otimes$”表示异或操作符。

NBI嵌入

生成的NBI序列可嵌入到加密音频中，从而消除传输开销。一个NBIk的大小取决于音频量化器的分辨率，即每个量化样本的比特数。$ t $ 比特的量化器会产生取值范围为1到 $ t $ 的NBIk，存储它需要 $ \lceil \log_2 t \rceil $ 比特。也就是说，NBIk可以用二进制形式表示为：
$$
NBI_k = \sum_{u=0}^{\lceil \log_2 t \rceil - 1} c_{k,u} \cdot 2^u.
$$
对于正常设置，$ \lceil \log_2 t \rceil $ 远小于帧大小 $ f $，一种将 $ \lceil \log_2 t \rceil $ 比特的NBIk嵌入到 $ F_k $ 的位图中的方法在算法2中给出。简而言之，$ F_k $ 中彼此不相邻的一些样本的最高有效位被NBIk的比特所覆盖。最低有效位用于数据隐藏，因此不作修改。

2.2 数据隐藏方

如图1所示，数据隐藏者的工作可分为以下两个步骤。

NBI提取

数据隐藏者首先通过逆向执行算法NBI来获得序列，即算法2，也就是算法3。

算法2

w ← ⌊f / ⌈log₂ t⌉⌋
for l = 0 to ⌈log₂ t⌉ − 1 do
    B̃ₖ,ₗ⋅w,ₜ₋₁ ← cₖ,ₗ
end for

算法3

w ← ⌊f / ⌈log₂ t⌉⌋
for l = 0 to ⌈log₂ t⌉ − 1 do
    cₖ,ₗ ← B̃ₖ,ₗ⋅w,ₜ₋₁
end for
NBIₖ ← Σ cₖ,ᵤ ⋅ 2ᵘ

数据嵌入

利用NBI序列和预先协商的数据隐藏密钥，数据隐藏者通过首先将帧内的所有样本（例如 $ F_k $）划分为两个互不相交的集合（根据数据隐藏密钥确定），即集合-0和集合-1，然后执行算法4来将隐写消息的每一位嵌入到加密音频的每一帧中，从而嵌入隐写数据。

算法4

if 要嵌入的比特为 0 then
    反转 Set-0 中所有样本的 NBIₖ 最低有效位
else
    反转 Set-1 中所有样本的 NBIₖ 最低有效位
end if

2.3 接收者端

如图1所示，接收者完成的工作可分为以下四个步骤。

NBI提取

接收者首先获取与数据隐藏者相同的NBI序列。

音频解密

利用内容所有者发送的加密/解密密钥 $ r_{k,l,u} $，接收者可以通过以下操作恢复明文：
$$
b_{k,l,u} = B_{k,l,u} \otimes r_{k,l,u}.
$$
正如张在[10]中所解释的，数据隐藏者在密文域中翻转的比特在解密后于明文域中仍将保持翻转。也就是说，
$$
b’ {k,l,u} = B {k,l,u} \otimes r_{k,l,u} = b_{k,l,u} \otimes r_{k,l,u} \otimes r_{k,l,u} = b_{k,l,u}, \quad u = 1, 2, …, \text{NBI} k,
$$
且满足以下方程：
$$
b’ {k,l,u} + b_{k,l,u} = 1, \quad u = 1, 2, …, \text{NBI}_k.
$$

从嵌入了NBI的受损版本中进行音频恢复

接收者在上述解密步骤之后，从NBI-受损版本中恢复音频。由于仅考虑最高有效位是否被修改，NBI嵌入导致的一个样本值的变化可能为 $ 2^{t-1} $ 或 0。基于自然信号的高空间相关性，提出了算法5。

算法5

w ← ⌊f / ⌈log₂ t⌉⌋
for l = 0 to ⌈log₂ t⌉ − 1 do
    v1 ← Σ bₖ,ₗ⋅w,ᵤ ⋅ 2ᵘ   for u = 0 to t−2
    v2 ← 2^(t−1) + Σ bₖ,ₗ⋅w,ᵤ ⋅ 2ᵘ   for u = 0 to t−2
    interp ← (Sₖ,ₗ⋅w−1 + Sₖ,ₗ⋅w+1) / 2
    if |v1 − interp| ≥ |v2 − interp| then
        bₖ,ₗ⋅w,t−1 ← 1
    else
        bₖ,ₗ⋅w,t−1 ← 0
    end if
end for

数据提取和音频恢复

在已知预先协商的数据隐藏密钥的情况下，接收者可以进一步提取隐写消息并完全恢复音频。然而，必须知晓NBI信息。相应的数据提取和音频恢复过程如下。

与数据嵌入过程相同，将解密音频分割为非重叠帧，并且每个帧根据数据隐藏密钥划分为两个互斥的集合集合-0和集合-1。为了从特定帧中提取嵌入的隐写位并联合恢复原始帧，通过比较该帧的两个修改版本的空间相关性来进行，如算法6所述。

算法6

given a frame Fₖ
F₀ₖ ← 反转 Fₖ 中 Set-0 的所有样本的 NBIᵢ 最低有效位
F₁ₖ ← 反转 Fₖ 中 Set-1 的所有样本的 NBIᵢ 最低有效位
if g(F₀ₖ) > g(F₁ₖ) then
    return 比特 1 和 F₁ₖ
else
    return 比特 0 和 F₀ₖ
end if

根据NBI的含义或算法1中的计算可知，具有较大 $ g $-函数值的帧恰好是算法1的步骤11中的 $ m $，其中 $ \text{NBI}_k $，而具有较小 $ g $-函数值的帧则是由内容所有者创建的原始音频帧。注意，在算法6中，$ g(F₀ₖ) $ 与 $ g(F₁ₖ) $ 之间不存在相等情况，因为 $ \tilde{F}_k $ 中的 $ g(\tilde{F}_k) > g(F_k) $ 已预先确定。

3 实验

3.1 评估

采用分段信噪比（segSNR）测试工具[13]和感知音频质量评估（PEAQ）软件[14]来测量隐写音频的客观质量下降。后者基于ITU-R BS.1387标准，并输出客观差异等级（ODG），该等级是一种损伤标度，其中“0”对应“不可感知”，“-1”对应“可感知但不令人烦恼”，“-2”对应“轻微烦人”，等等。

3.2 实验设置

我们准备了10段20秒长的单声道音频片段（参见表1），包括语音、流行歌曲、新闻、器乐音乐等，作为宿主音频，并使用由‘0’、‘1’组成的随机序列作为隐写数据来测试我们的算法。每段宿主音频的采样率为44100，包含16位样本。

函数 $ g $ 和帧大小 $ f $ 是需要调整的两个主要因素。前者根据图1中方案的基本目标确定：实现隐写音频的质量下降最小化。翻转某些样本的最低有效位可被视为一种理想的数据隐藏方法，因为它为试图非法提取音频中隐藏信息的攻击者提供了较小的线索。基于该方法，更小的NBI意味着更小的质量下降，因此我们选择能为每一帧产生更小 $ g $ 值的函数以获得更小的NBIk。考虑到自然音频的平滑度特性，式(8)是一个候选方案，它计算离散信号二阶导数绝对值的求和。同样地，
$$
g_n(A) = \text{sum}(\text{abs}(d^{(n)}(A)))
$$
计算离散信号的 $ n $ 阶导数绝对值的求和。在式(14)中，当 $ n $ 增大时，会引入更多邻近样本作为参考。

如图3所示，NBI随着 $ n $ 的增大而减小。我们在此选择 $ n = 4 $ 以兼顾可接受的质量下降（见图4）和计算效率。固定函数 $ g $ 后，帧大小 $ f $ 可进一步调整。直观上，隐藏容量和/或嵌入率EBR(比特/样本)将随 $ f $ 的减小而增加，即
$$
\text{EBR} = k \cdot \frac{1}{f},
$$
其中 $ k $ 是比例常数，且为了不失一般性，我们可以在接下来的讨论中设 $ k = 1 $。然而，如果NBI序列的长度增加，将会引入更多的通信成本和信息泄露。

我们在这里使用NBI率NBIR（比特/样本）来表示额外的通信开销，并且我们有
$$
\text{NBIR} = \frac{4}{f} = 4 \cdot \text{EBR},
$$
因为每个NBI占用4比特。当然，如果使用霍夫曼编码对NBI序列进行编码，则上述开销将进一步降低。为了便于比较，表2给出了每个测试音频在 $ g_4 $ 和 $ f = 50 $ 情况下的熵（即NBI的理论最优平均码长）。

如图4所示，随着 $ f $ 的减小，隐写音频的质量下降变得更加明显。我们在此选择 $ f = 30 $ 以提供可接受的质量下降、效率和零误码率。

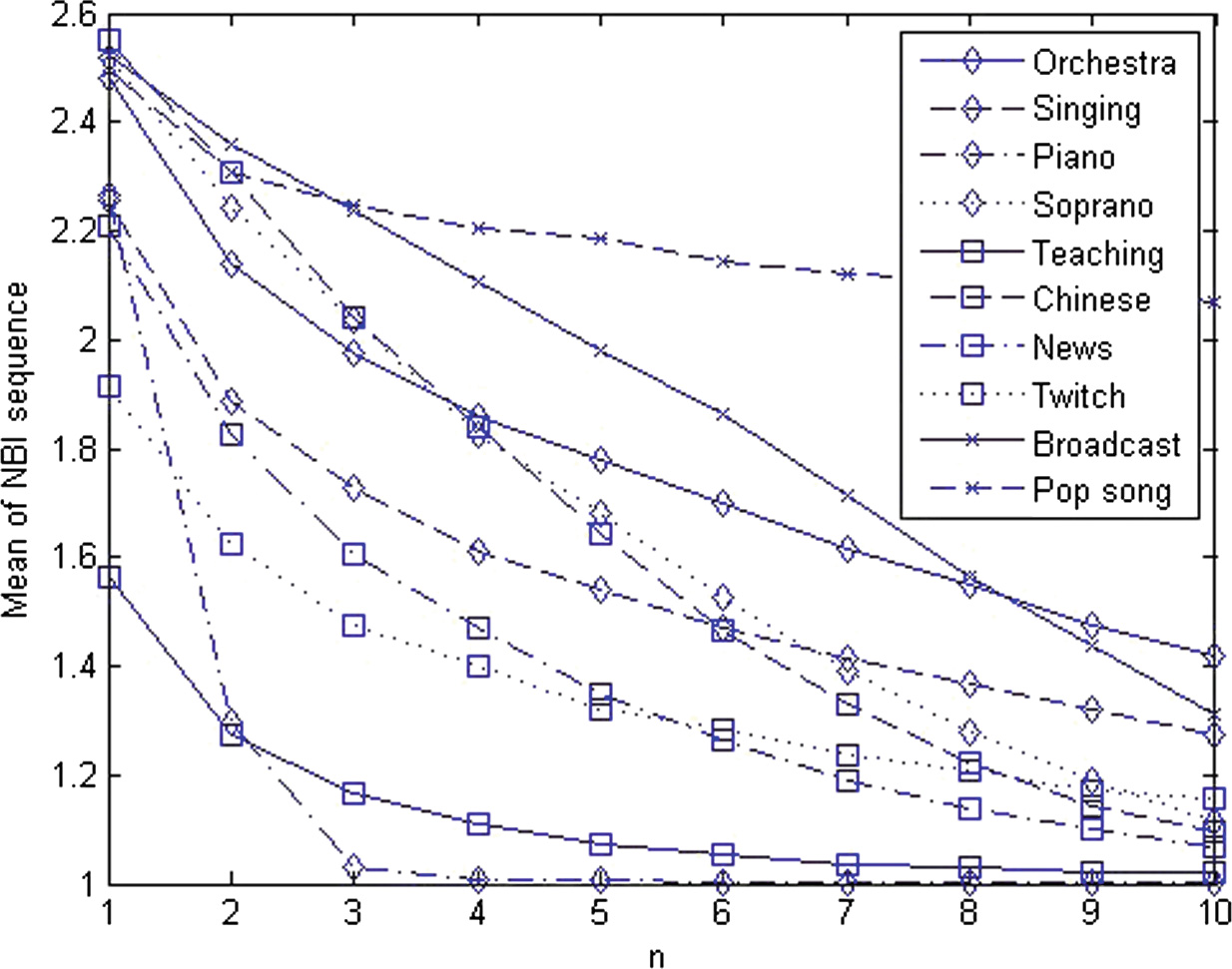
10个测试音频的 NBI序列均值，对应 $ n $，见公式(14)，帧长50。

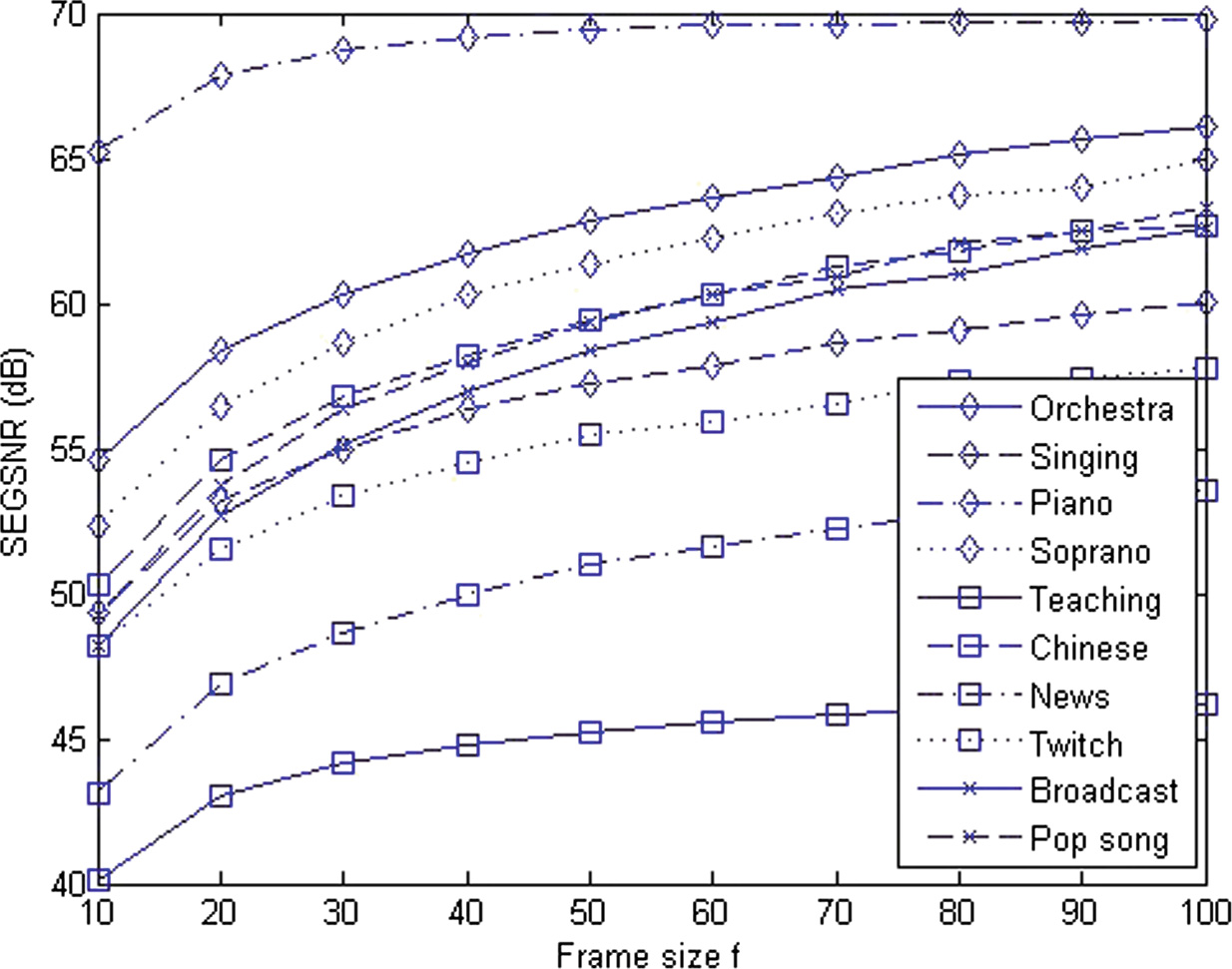
在10个测试音频片段上（见表1）分段信噪比随帧长的变化，其中函数由公式(14)定义。

表2. 每个测试音频在 $ g = g_4 $ 和 $ f = 50 $ 条件下的 NBI 的一些概率和熵值

索引	P{NBI= 1}	P{NBI= 2}	P{NBI= 3}	熵(比特)
1	0.5502	0.2079	0.1272	1.8265
2	0.6403	0.1962	0.0998	1.5334
3	0.9906	0.0093	0	0.0765
4	0.5787	0.2027	0.1074	1.8007
5	0.9234	0.0539	0.0146	0.4871
6	0.5485	0.2115	0.1312	1.8014
7	0.6694	0.2239	0.0800	1.3197
8	0.7523	0.1450	0.0665	1.1865
9	0.5115	0.1930	0.1176	2.0694
10	0.5070	0.1858	0.1177	2.1624

3.3 结果

给定 $ g_4 $ 和 $ f = 30 $，表3显示了10个测试音频的实验结果。

表3. 对应于给定的10个测试音频 $ g = g_4 $ 和 $ f = 30 $ 的隐写音频的质量测试。同时显示误码率和嵌入率

Tag	segSNR(dB)	ODG	误码率	EBR(bps)
管弦乐队	60.30	0.011	0	0.0333
歌唱	54.91	-0.063	0	0.0333
钢琴	68.74	-0.020	0	0.0333
女高音	58.60	-0.308	0	0.0333
教学	44.18	-0.058	0	0.0333
中文	56.76	-0.138	0	0.0333
News	48.62	0.069	0	0.0333
Twitch	53.36	0.017	0	0.0333
广播	55.12	-0.113	0	0.0333
流行歌曲	56.39	-0.500	0	0.0333

3.4 在音乐数据库上的测试

我们进一步在公开可用的RWC音乐数据库上评估了我们的方法[15]，其中包含100种不同类型的音频（单声道，16位/样本，采样率为44100）。我们发现，在某些音频中可能存在较小的帧数不足，无法提供足够的NBI（如果帧大小不够大）。为解决此问题并保持可接受的容量，在这种情况下我们采用一个小的附加技巧（设置NBI= 0）。

在进行数据嵌入时，不再根据NBI反转最低有效位，而是反转固定数量的最低有效位，使样本远离原点。在数据提取时，计算样本与其原点之间距离的求和值进行比较，求和值较小者被判定为原始帧。

为了实现零误码率，我们设置 $ g_4, f = 50 $ 并在NBI= 0时反转7个最低有效位。图5和图6分别显示了在RWC数据库上进行的分段信噪比和客观差异等级结果。

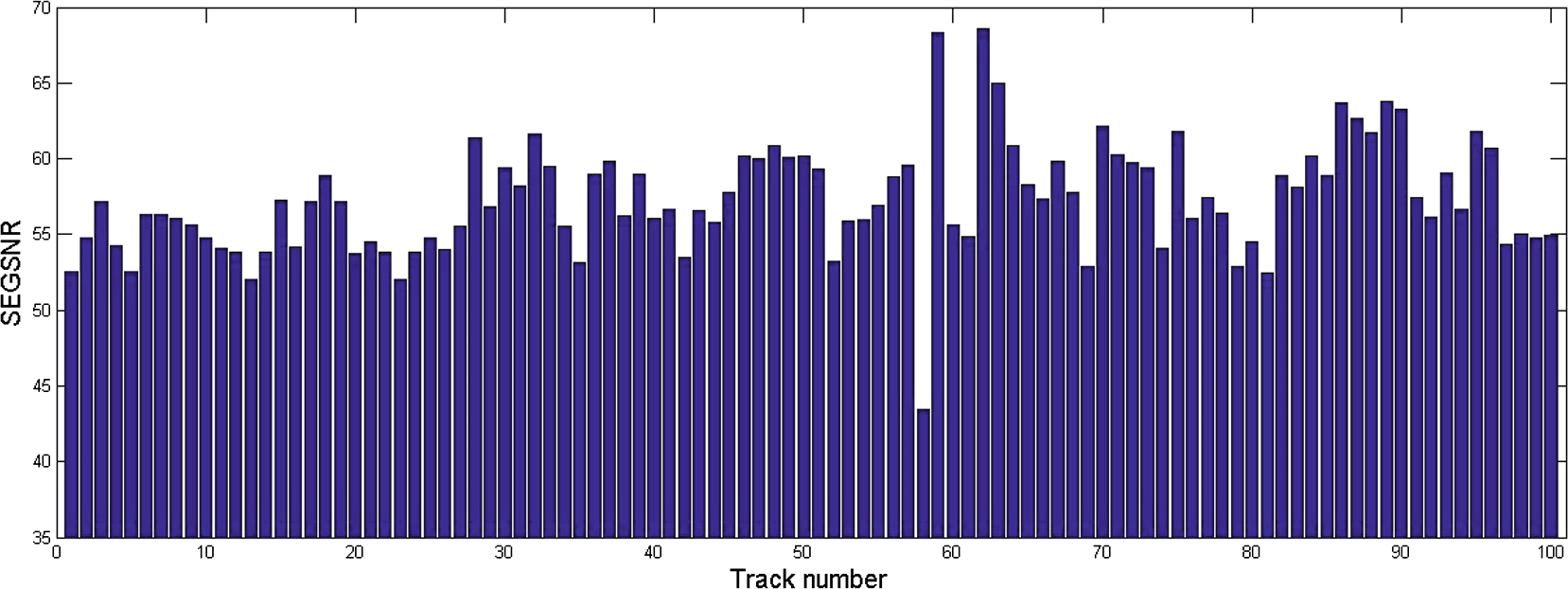
RWC音乐数据库中100个音频的分段信噪比。

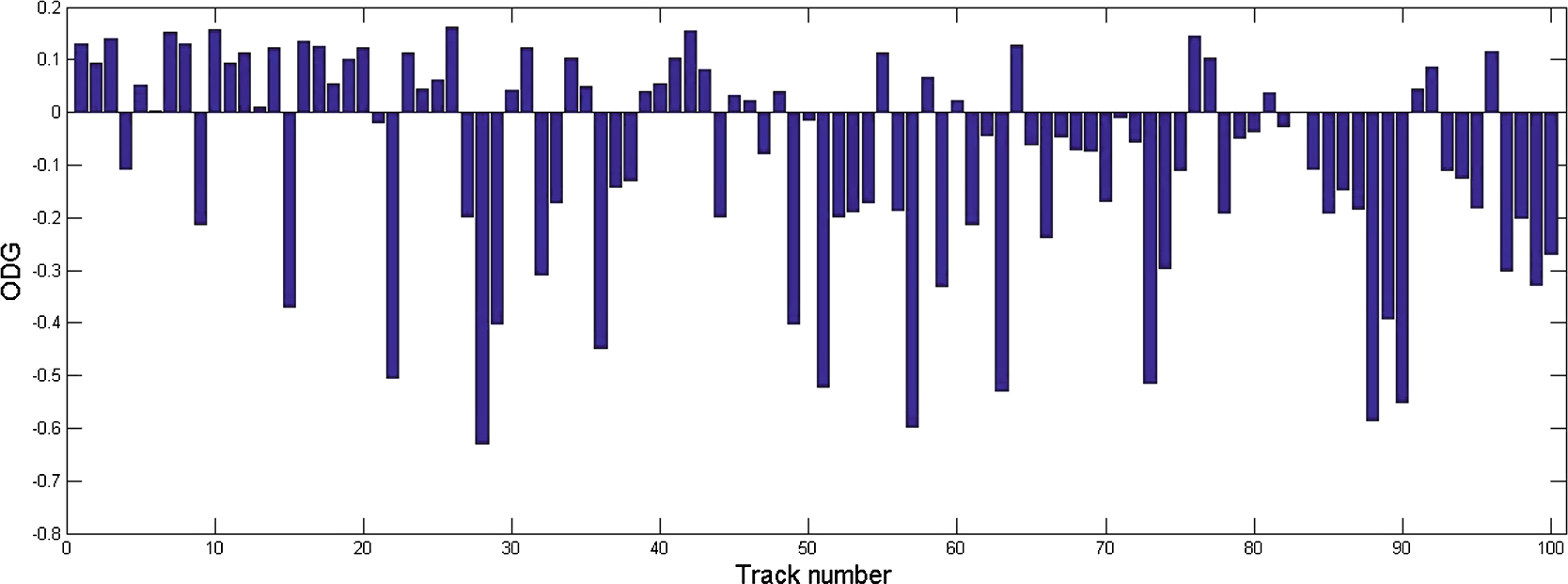
RWC音乐数据库中100个音频的客观差异等级。

4 结论

本文提出了一种新的用于加密音频的可逆数据隐藏方法。利用NBI信息，即使数据隐藏者不了解原始内容，仍能将隐写数据理想地嵌入到加密音频中。在解密和恢复过程后，由隐写数据引起的缺陷几乎不可察觉（平均ODG约为-0.09，如图6所示）。如果接收者拥有预先协商的数据隐藏密钥，则可以进一步无误差地恢复原始音频并提取隐写消息。

如上所述，NBI信息在整个过程中起着重要作用。NBIk随帧 $ F_k $ 自然度变化的值将使 $ F_k $ 或音频的质量下降限制在较小范围内。NBIk可被视为信号段的一个特征，而NBI序列的熵可被视为整个音频的一个特征。NBI序列熵的物理意义及其可能的应用值得进一步研究，当然也是我们未来的研究方向之一。

非法接收者在执行解密过程之前提取隐写数据的可能性是未来工作中另一个有趣的话题。