隐私感知的智能家居数据上传优化

隐私感知的传感器数据上传管理以安全接收智能家居服务

摘要

近年来，配备大量传感器和物联网设备的智能家居已广泛普及。然而，当智能家居用户享受老年人监护等智能家居服务时，需要将隐私敏感数据上传至可能不受信任的云服务器，而服务质量（用户收益）取决于上传数据的数量/频率。本文旨在最小化隐私泄露风险并最大化用户通过服务获得的收益，提出一种新颖的隐私感知数据管理方法，该方法应用于由配备传感器的智能家居、边缘计算服务器和云服务器组成的智能家居系统。我们构建了一个组合优化问题，综合考虑边缘服务器资源约束、用户预算以及活动的k‐匿名性和用户偏好，在每个时隙中确定最优的数据类型（原始数据或在边缘识别的活动标签）和上传频率的选择。由于该问题是NP难的，我们提出一种启发式算法，以贪心方式选择目标函数值更优的方案，从而获得半最优解。通过使用智能家居开放数据集进行实验，我们验证了建议方法优于仅使用云服务器的传统方法。

Index Terms— 智能家居，隐私，风险，收益，优化

一、引言

智能家居由多种传感器和电器组成，以支持自动生活日志。大多数智能家居系统将数据存储并在具有大容量内存和强大处理器的云服务器[1]–[3]中进行处理。尽管该方法已被广泛采用，但在将大量智能家居的数据传输到云服务器[4]时，仍存在较大的延迟和功耗问题。因此，边缘计算或雾辅助的云计算环境因其能够减轻云服务器和广域网[5]–[8]的负载与延迟而受到广泛关注。此外，在基于云的方法中，数据在可能不可信的云服务器1,上被存储/累积并随后进行处理/分析，因而存在数据泄露的潜在风险。

这可能导致隐私泄露，因为攻击者可以利用诸如定位数据、家用电器功耗等有意义的数据，通过机器学习[9]构建模型以重新识别用户。为应对该问题，可采用全同态加密（FHE）技术[10]，该技术能够在不解密的情况下对数据执行算术运算，从而实现

我们假设存储在云服务器中的数据可能会因网络攻击、管理员疏忽管理等原因而泄露。

在云服务器上使用机器学习进行活动识别、异常检测等安全操作。然而，全同态加密（FHE）需要巨大的计算能力，难以在实现智能家居服务时实际应用。

为了保护用户的隐私，我们假设用户通过上传在家庭中感知到的数据来获得服务，且上传的数据可能会发生泄露。因此，必须考虑从泄露的数据中对用户进行重新识别的风险。在[11],中，我们提出了一种威胁模型，攻击者可以通过从外部短时间物理观察用户家庭中的活动，并将其与存储在不可信云服务器上的活动数据进行匹配，从而重新识别用户。然而，如果在同一个时隙内，多个家庭中发生的相同日常生活活动（ADLs）数量较多，则相较于数量较少的情况，攻击者更难识别用户（例如，中午有30个智能家居用户都在“吃午饭”，比仅有2个用户在“工作”更难以区分）。这一理念被称为 k-anonymity[12]。

在本文中，我们提出了一种新颖的隐私感知数据管理方法，用于由三部分组成的智能家居系统：配备传感器的智能家居、边缘计算服务器和云服务器。利用边缘服务器的好处不仅在于减少传输延迟和计算时间，而且与基于云的方法相比，通过仅向云端发送分析结果并丢弃原始数据，降低了用户被重新识别的风险。为了在保持服务收益的同时保护隐私，我们采用了以下思路：（i）上传数据类型（原始数据或在边缘识别的活动标签）和上传频率的选择；（ii）基于时隙的风险与收益评估；（iii）在服务持续时间内（例如1天、1周等）每个时隙中综合权衡风险与收益后作出最优选择决策。

我们将该问题建模为一个组合优化问题，以输出每个时隙中数据类型和上传频率的选择，同时考虑边缘服务器资源和用户预算的约束，以及活动的k‐匿名性和用户偏好。我们还提出并开发了一种启发式算法来求解半最优解。

此外，我们使用智能家居开放数据集CASAS[13]来评估建议方案。我们将建议方法的性能与两种传统方法进行了比较（即不使用边缘服务器的建议方法和另一种方法）

II. 相关工作与挑战

用户的隐私问题促使大量研究人员提出多种具有隐私评估功能的智能家居系统。在[14],中，Chakravorty提出了一种智能家居框架，该框架通过基于启发式的k匿名化算法来保护聚合数据中的个人标识符。

在考虑与隐私相关的控制优化方法时，一些研究聚焦于隐私保护与资源消耗之间的优化。例如，Yang[15]提出了一种隐私保护方法，用于保护能耗数据中的活动存在性，并通过使用在线算法提出了隐私保护与成本之间的优化。[16], Park通过实施虚假活动来防御基于指纹和时序的窃听（FATS）攻击，实现了隐私保护，并提供了隐私保护与能效之间权衡的优化。Zhang的工作[17]中发现了个体隐私与系统性能之间权衡的优化，该研究在给定的差分隐私要求下构建了一个优化问题。此外，Liu[18]提出了一种针对流量分析攻击的差分隐私框架，并考虑了能耗和资源约束。在具有社区层级结构的基于云的智能家居系统中，Lee[19]通过将智能家居数据类型划分为识别值、敏感数据和非敏感数据来实现隐私保护，并考虑了智能家居数据分析所带来的收益。

据我们所知，目前尚无物联网系统在考虑预算和资源约束的同时，兼顾风险与收益之间的权衡。

III. 隐私感知传感器数据上传的建议方法

A. 智能家居系统概述

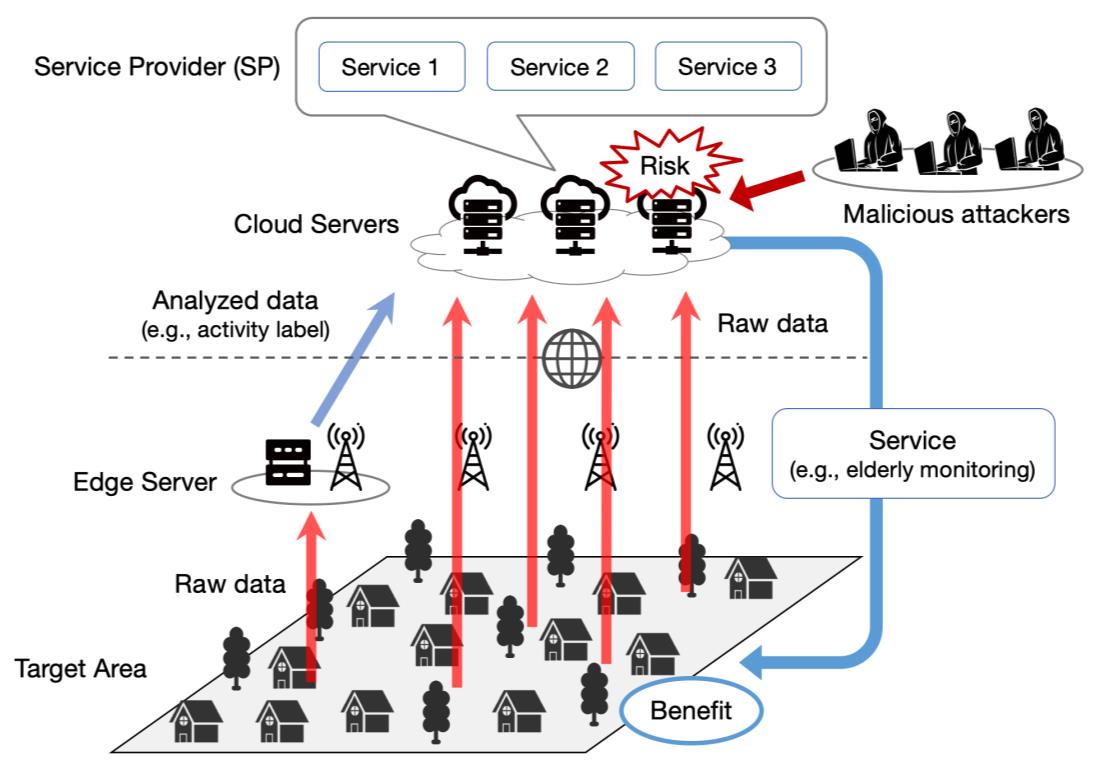
我们假设的智能家居系统由三部分组成：智能家居、边缘计算服务器和云服务器，如图1所示。每个智能家居都配备有多种类型的传感器、执行器和电器，在居民生活期间生成原始数据，并将这些数据上传到服务器。在我们的系统中，存在两种类型的服务器：云服务器和边缘服务器。云服务器作为中心化服务器，用于训练/应用活动识别模型，并提供老年人监护、活动生活记录、异常检测、上下文感知服务等服务。边缘服务器则在本地端执行隐私感知数据处理，将原始传感器数据转换为活动标签。

B. 威胁模型

如图1所示，我们假设不可信云服务器可用于提供智能家居服务，并且将来自智能家居的数据存储和累积到云服务器时存在潜在风险。由于服务提供商内部或外部的攻击者可能窃取敏感数据，一些关注隐私的住户可能不愿意上传他们的数据。另一方面，不关心隐私的住户可能更愿意上传所有数据以获得服务提供商的完整服务。然而，如果攻击者能够访问他们上传的数据，则他们面临被重新识别的风险。

C. 假设

1) 关于目标区域、家庭和活动的假设：

设 A表示目标住宅区， H表示区域 A内的智能家居集合。下文中，家庭、住户、用户和居住者术语可互换使用，并用 h ∈ H表示。当居住者在每个家庭 h ∈ H中时，可能发生的活动类型集合为 Act 。设 T={τ1, τ2,…, τn}表示一天中的时间槽集合。例如，我们将一天的时间划分为8个时间段：(0‐3)、(3‐6)、(6‐9)、(9‐12)、(12‐15)、(15‐18)、(18‐21)、(21‐0)。在家庭 h中，活动 Act在时隙 τ期间产生的数据包括传感器数据。

2) 货币成本和预算的假设：

我们假设每个家庭在上传数据/使用边缘服务器以接收服务时需支付一定成本。预算根据每个家庭的情况而定，家庭 h的预算用 Budgeth表示。每个用户 h在将数据上传到云服务器时都必须支付一定成本。此处，当用户使用边缘服务器分析原始数据并将分析后的数据（活动标签）上传至云服务器时，所需支付的成本更高，因为边缘服务器的资源量有限。令x h,τ ∈{raw, label}表示用户选择上传原始数据或标签数据（通过使用边缘服务器）到云服务器的选择。

此外，在每个时间槽中，成本不仅取决于边缘资源的使用情况，还取决于在该时间槽内使用的频率。我们用yh,τ表示频率，用 Cost money( x h,τ, yh,τ)表示成本。所有时间槽累积的成本总和 T不得超过每个家庭 h ∈ H的预算Budgeth 。支付所带来的好处

3) 关于风险、收益和计算成本的假设：

我们假设，当智能家居数据在时隙 τ传输到云端时，每个住户 h的隐私泄露风险由 R(h, τ)表示。该风险取决于四个因素：数据类型、上传频率、用户偏好以及k‐匿名性。

关于数据类型，假设原始数据比标签数据具有更高的隐私风险，因为原始数据包含的信息比标签数据更丰富。例如，当用户在打开灯光的同时洗澡时，通过物理观察及其数据状态，原始传感器数据容易重新识别出用户。考虑到上传频率，假设较高的上传频率比低上传频率具有更高的风险。设 r(x, y)表示用户选择数据类型 x和数据上传频率 y时的潜在风险。

此外，用prefh,τ表示的用户偏好反映了用户 h在时隙 τ期间接收服务的精确程度。具体而言，用户需要决定其希望在该时隙内对活动进行监控的频率。由于用户无法直接指定频率，系统将根据用户设定的偏好后续确定该频率。例如，在老年人监控服务中，如果用户希望夜间被监控的时间间隔比白天更短，则该偏好将在图2中设置为 “h0”。鉴于用户设定的不同偏好级别，我们可以假设高偏好时隙可能包含敏感数据。因此，当时隙的偏好越高时，该时隙中的风险也越高。

关于 k‐匿名性，如果过去某个活动在时隙 τ发生的 k值足够大，则可以降低风险。换句话说， k值与隐私风险成反比。

令 u(x, y)表示数据粒度为 x、上传频率为 y时上传数据的效用。令 B(h, τ)表示智能家居 h中的居住者在时隙 τ内从服务中获得的收益。该收益 B(h, τ)可以

可以被视为每个住户 h 上传数据的效用 ux, y。然而，上传频率的差异会影响效用 ux, y，因为较高的上传频率可能激励服务提供商构建/提供更精确和有效的服务。此外，用户偏好prefh,τ也会影响收益，因为居住者可能希望在特定时间槽获得更好的服务，而对其他时隙的服务质量不关心。

此外，我们假设当数据被发送到边缘服务器以获取活动标签时，边缘服务器会消耗计算成本Costcomp(xh,τ, yh,τ)。而且，在不同的上传频率或时间粒度下，上传的数据量xh,τ越大，计算成本的总和就会显著增加，但其总和在每个时隙 τ内不得超过本地边缘服务器资源 LocalResource的容量。

D. 问题表述

为了构建优化问题，表I中提供了符号表示。

变量	定义
a ∈ A	目标住宅区
h ∈ H	目标区域的住户 a τ ∈ T 活动发生的时间段
act(h, τ)*	过去在 τ进行的活动类型集合 h
xh,τ ∈{raw, label}	数据粒度
yh,τ	时间粒度。例如，每10秒、5分钟或1 小时可以作为上传频率。
prefh,τ* ∈[0, 1]	用户 h在该时间段上传数据的偏好时隙 τ
k(act(h, τ) τ)* ∈[0, 1]	活动类型的k‐匿名性因子，即 h在 τ进行的活动过去
r(x, y)* ∈[0, 1]	数据粒度的潜在风险
u(x, y)* ∈[0, 1]	数据 r(x, y)在每个x和y处的可用性（带来的收益程度） 通过提供数据，经由服务接收
Cost comp(xh,τ, yh,τ)*	粒度为 x和 y的数据的计算成本 单位时间
Cost money(xh,τ, yh,τ)*	粒度为 x和每单位 y的数据的货币成本 时间
LocalResource	目标区域的总计算资源 a ∈ A
Budgeth	每个住户的总预算 h

1) 风险函数：

风险函数 R(h, τ) 表示当用户选择数据粒度 x和时间粒度y时的潜在风险。基于对风险的假设，可定义如下：

$$
R(h, τ)= \frac{r(x, y) \cdot pref_{h,\tau}}{k(act(h, τ), τ)}
$$

2) 收益函数：

收益函数 B(h, τ) 表示用户从服务中获得的服务效益，即由智能家居数据产生的服务效用。因此，其表述如下：

$$
B(h, τ)= u(x, y) \cdot pref_{h,\tau}
$$

3) 约束：

在此问题描述中，需要考虑两个约束：计算成本和货币成本。每个时隙 τ 上所有选择的计算成本之和必须小于或等于该时隙的本地边缘资源总量 LocalResource。

因此，可以定义计算成本约束：

$$
\forall\tau \in T, \sum_{h\in H} cost_{comp}(x_{h,\tau}, y_{h,\tau}) \leq LocalResource
$$

此外，我们考虑每个家庭 h所选选择的货币成本。因此，货币成本约束可以定义为：

$$
\forall h \in H, \sum_{\tau\in T} cost_{money}(x_{h,\tau}, y_{h,\tau}) \leq Budget_h
$$

4) 目标函数：

为了在用户的风险与收益之间实现最优权衡，我们推导出公式(1)和(2)，将目标函数定义如下：

$$
\text{Maximize } \alpha\sum_{h\in H}\sum_{\tau\in T} B(h, τ)−(1−\alpha)\sum_{h\in H} \sum_{\tau\in T} R(h, τ)
$$

subject to (3)−(4)

其中 α表示收益函数的权重因子（介于0和1之间）， 1−α表示风险函数的权重因子。我们假设 B和 R均在 0到1之间进行了归一化处理。

E. 优化算法

上一节中提出的优化问题是一个组合优化问题，预计是NP难的，因为它是多维背包问题的一个特例，而该问题是NP难的[20]。因此，我们采用启发式优化算法算法 1来求解半最优解。

算法1 启发式优化算法

1: 输入: HT ← H × T, C← X × Y, Ch∗ ← ∅, NCh← ∅ ∀h ∈ H, TotalCostτ ← 0 ∀τ ∈ T
2: 输出: C ∗ h , h ∈ H
3: 当 HT ≠ ∅ 执行
4: 对每个 h ∈ H 执行
5: (ch , τ h) ← 获取最佳时隙选择(h, C, NC h)
6: 如果 Cost(c) ≤ Budgeth ∧ TotalCostτ+ Cost(c) ≤ MaxResource τ 然后
7: C ∗ h ← C ∗ h ∪{(ch , τ h)}
8: TotalCost τ ← TotalCost τ + Cost(c)
9: Budgeth ← Budgeth − Cost(c)
10: HT ← HT(h, τ)
11: else
12: NC h ← NC h ∪(ch , τ h)
13: 结束如果
14: 结束循环
15: 结束循环

在算法1中，对于每个家庭 h，选择目标函数值最高的选择 c h和时隙 τ h的组合（第4–5行）。该选择的搜索通过函数 GetBestSlotChoice完成，如算法2所示，该算法用于为家庭 h找到目标函数值最大的选择和时隙组合。第4行中的ObjectiveFunction是公式5中定义的函数。

算法 2 用于寻找最佳时隙和选择组合的算法

1: 函数 获取最佳时隙选择(h, C, NCh)
2: ch← 0, τh← 0, fh← 0, CT ← C × T
3: 对于每个 (c, τ) ∈ CT\NCh 执行
4: f← 目标函数(h, c, τ)
5: if f > fh then
6: fh← f, ch← c, τh← τ
7: end if
8: 结束循环
9: return (ch, τh)
10: 结束 函数

在算法1的第6–12行中，检查约束条件。然后采用该选择，并计算该时隙的边缘资源总成本时隙 τ和家庭 h的预算在满足约束条件时被更新（第8‐9行），并且当前家庭与时隙的配对将从HT中移除（第10行）（第 6行）。否则，该选择会被包含进 NCh，以防止集合中的项目未被选中。因此，在下一次搜索中，该选择与时隙的配对不会被选中用于 h（第11‐12行）。此过程以贪婪方式重复进行，直到所有家庭h以及时隙 τ的配对都被分配了选择（第3‐15行）。

四、评估

A. 评估场景

1) 智能家居场景的定义：

为了评估我们的建议方法，我们使用来自CASAS的公开数据集[13]设置了目标区域和智能家居。我们选择了名为“hh101”的数据集，该数据集包含一个住户在60天实验中的数据，涉及76种传感器数据和30种活动标签。为了将该数据集应用于我们的场景，我们将一个住户的60天实验数据视为60个住户的一天数据，以考虑活动的 k‐匿名性。此外，所有住户根据预算金额被划分为3个组。

2) 仿真配置：

我们在表II中展示了实验所用的参数。如前所述，我们有60个住户/用户（即 |H| = 60），其中一些参数（如风险值和效用值）具有不同的假设值，以便根据假设区分每个上传决策。

参数	值（们）
住户数量 (|H|)	60
高、中、低预算家庭的数量	20, 20, 20
每个高、中、低预算家庭的初始预算 (Budget h)	600, 300, 150
每个时隙的总边缘资源 (LocalResource)	2000
以高、中、低频率上传原始数据的风险值	64, 32, 16
以高、中、低频率上传标签数据的风险值	8, 4, 2
以高、中、低频率上传的效用值（原始数据与标签数据之间无差异）	80, 40, 20
每种低、中、高上传频率的上传成本（标签）	60, 30, 6
每种低、中、高上传频率的上传成本（原始）	40, 20, 4
高、中、低偏好的取值	0.25, 0.5, 1.0
加权系数 (α)	0.6

B. 结果

本节描述了建议方法的评估结果，并将其与两种传统方法的结果进行比较：云1（风险感知的基于云的方法，与建议方法相同但不使用边缘服务器获取活动标签）和云2（非风险感知）

基于云的方法，该方法与风险感知的基于云的方法相同，但其目标函数仅为最大化收益。

图3显示了三种方法在三个预算类别下的目标函数值。建议方法在所有预算类别中均优于传统方法。相反，云2（非风险感知的基于云的方法）导致最低目标函数值。从图4可以看出，我们的建议方法在所有预算组中为每个住户实现了最高的目标函数值。

此外，建议方法得出的选择比传统方法具有更低的风险和更高的效益值。尽管使用k‐匿名性来降低风险值，但其他因素的影响也有所体现（见图5）。

图6展示了三种方法在三个预算类别和三种偏好下时间槽的平均风险和效益值的比较。建议方法与其他方法的收益相似，但风险远低于其他方法。云1（部分风险感知）的结果优于云2（无风险感知），但差异不大。

图7中对原始数据和标签数据上传的三种不同风险比率（8:1、4:1、2:1）的比较表明，较高的风险比率在不同的上传频率下更倾向于标签选择而非原始数据选择。原始数据选择在1:4的比率下逐渐增加，并在1:2的比率下达到最多，且在不同的上传频率选择中表现更为多样。这意味着不同的风险比率会影响各预算组之间的选择。

V. 结论

在本文中，我们首先定义了威胁模型，即智能家居用户隐私可能因将所有传感器数据上传至不可信的云服务器以获取自动生活日志和老年人监护等智能家居服务而遭到侵犯（通过重识别攻击）。此外，我们发现，在限制数据上传时，隐私保护与所获得的服务效益之间存在权衡。同时，我们提出了一种新颖的隐私感知的传感器数据上传管理方法，该方法可最小化隐私泄露风险，并最大化用户所获得的服务效益。建议方法的创新之处在于利用边缘服务器，仅将分析后的数据上传至云服务器，从而降低上传原始数据带来的风险。

通过使用CASAS智能家居开放数据集进行的实验，我们证实了建议方法优于仅利用云服务器或未考虑风险因素的传统方法。因此，我们发现通过类似我们所提出的基于信息技术的系统来支持用户在数据上传方面的决策非常重要。