基于混沌映射的图像加密

基于混沌映射的彩色数字图像加密技术及软件实现

1. 引言

随着网络技术和多媒体技术的快速发展，多媒体通信已成为获取信息的重要手段，它已经成为人们生活中不可或缺的一部分：各种形式的数字信息通过网络进行便携式快速传输，电子商务、电子政务通过它为我们提供了多种服务，但同时也带来了信息安全风险问题[1]。据统计，全球几乎每20秒就发生一次黑客入侵事件，根据美国联邦调查局调查，仅美国每年因信息安全问题造成的经济损失就超过170亿美元[2]。如今，信息安全技术不仅关系到个人通信隐私、企业的商业秘密乃至企业的生存，还关系到一个国家的安全性[3, 4]。因此，信息安全技术正受到全社会越来越广泛的关注[5]。

随着多媒体技术、信息存储技术的快速发展以及网络带宽限制的放宽，越来越多的数字图像通过互联网传输，并逐渐成为获取信息的重要手段[6‐9]。网络上的图像中，有些包含无关信息，而有些则至关重要，可能涉及个人隐私、企业利益、军事机密和国家安全。另一方面，互联网的普及以及互联网技术的发展使得这些图像信息易于被访问和收集，无论这种收集是善意还是恶意、合法还是非法，其安全性传输逐渐成为公众关注的问题，图像传输的可靠安全处理也成为当前研究的重要方向[10, 11]。

目前图像加密技术的研究主要集中在同一空间内对图像进行重新编码，即图像置乱加密技术。通常通过增加密钥长度和多重加密循环等方式来提高抗破译能力。另一种方法是将加密后的图像、密度图和密钥存储在不同的空间中，即基于秘密共享的秘密图像分割与加密技术。从当前研究来看，这类加密算法具有有效性且难以解密。本文提出了一种基于混沌映射的数字彩色图像加密算法。该算法结合了灾变与混沌映射，提出了基于Logistic映射的彩色图像加密算法，并对两种加密算法进行了性能比较与分析。

2. 数字图像加密技术与密码系统

A. 密码系统

图像加密密码起源于早期的经典理论，该理论对现代密码学的发展具有重要作用。图像加密密码系统通常被称为密码文，其框图如图1所示，由五个部分[12]组成：

加密器	( ) , e C f M K 	解密器
加密密钥Ke 发送方		解密密钥Kd 接收方
		1 (C, ) d M f K − =

(1) 明文空间M，即所有明文的集合；
(2) 密文空间C，即所有密文的集合；
(3) 密钥空间K，即所有密钥的集合，密钥K通常由加密密钥Ke和解密密钥Kd组成；
(4) 加密算法E，即由M到C的加密变换，称为加密函数f(.)；
(5) 解密算法D，即通过从C到M的逆向变换进行解密，其中M=f(c, kd)为解密函数，要求f(.)为可逆函数。

B. 数字图像及其数学表示

从视觉角度来看，图像是一种通过各种不同形式和手段观察客观世界而获得的间接效果，能够直接或客观地反映自然景物或事物实体，从而在人眼中产生视觉感知。它是人们自出生以来获取最重要且最丰富的信息的最大对象[14]。

首先，最直观的方法是使用二维矩阵来表示数字图像，其中矩阵的行和列的元素即为各个像素的值。数字图像的元素显示在计算机屏幕坐标像素点上，该矩阵对应于数字图像中像素灰度值（通常为256）或颜色值[15‐17]的位置。例如，一个Ge x 像素的数字图像，其像素灰度值或颜色值由行列矩阵Ge F表示，如图2所示：

C. 数字图像的基本统计

(1) 图像信息量
如果一幅图像有q个灰度值，其概率分别为p₁, p₂, p₃,…,pi，根据香农定理，该图像的信息量由公式(1)给出：

$$
H = -\sum_{i=1}^{q} p_i \log_2 p_i \tag{1}
$$

H通常称为熵，当图像中各灰度值出现的概率相等时，图像的熵达到最大值。例如，一个8位数字图像的信息量可用公式(2)表示：

$$
H = -\sum_{i=0}^{255} p_i \log_2 p_i \tag{2}
$$

(2) 图像平均灰度
表示图像中所有像素灰度值的平均灰度的算术平均值，它反映了不同物体图像的平均反射强度，通用公式(3)：

$$
\bar{f} = \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} f(i,j) \tag{3}
$$

(3) 图像灰度方差
方差反映了图像中各像素灰度值相对于图像平均灰度的离散程度总值，是衡量图像信息熵大小的主要度量之一，也是图像统计特性中最重要的统计量。图像信息量越大，方差越大，按公式(4)计算。

$$
\sigma^2 = \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} (f(i,j) - \bar{f})^2 \tag{4}
$$

范围是图像灰度值的最小值与最大值之间的差值，即

$$
\text{range} = \max(f(i,j)) - \min(f(i,j)) \tag{5}
$$

3. 基于混沌映射的彩色图像加密算法

A. 混沌映射模型

一维混沌多项式模型可以用以下N次的比值表示：

$$
T_{N+1}(x(n)) = 2\alpha T_N(x(n)) - (1-\alpha)^2 T_{N-1}(x(n)) \tag{6}
$$

取模型范围为[0,1]，存在一个控制参数α，其表示为切比雪夫多项式类型，n表示时间，N是大于1的整数。

Xn(N+1) 是 N−1阶模型映射，因为在区间 [0,1] 内有 N−1 个极点。根据施瓦茨导数定理，我们可以看到 X(n + l) 最多具有 N + 1 周期吸引轨道。该映射在单周期内具有最稳定的固定点，或者说是遍历性的。

映射的不变测度公式如下：

$$
\mu(x) = \frac{1}{\pi \sqrt{x(1-x)}}, \quad 0 < x < 1 \tag{7}
$$

公式(7)中，参数α的(n + 1)可以表示如下：

$$
\alpha = \frac{\sum_{k=0}^{N-2} C_k^{(N)}}{\sum_{k=0}^{N-1} C_k^{(N)}} \tag{8}
$$

本文提出了一种基于灾难协同混沌模型的新型彩色图像加密算法：

$$
\begin{cases}
x_1(n+1) = \tan(3 \arctan(x_1(n))) \
\Phi_{3,3,2}(x_1,x_2,x_3) = \tan(3 \arctan(x_2(n))) \
x_3(n+1) = \tan(2 \arctan(x_3(n))) \cdot f(x_1(n),x_2(n))
\end{cases} \tag{9}
$$

B. AES加密算法，解密算法

AES加密算法的解密流程图如图3所示。可以看出，在解密时，只需将加密过程中执行的所有操作进行逆向操作，并采用逆向方案和密钥调度即可。AES算法具有其自身特性，即解密与加密具有基本相同的结构，因此存在逆等效密码，这相当于通过一系列逆变器变换将原始交换AES算法逆码化以实现解法，这些逆变换按与 AES加密算法相同的顺序执行。

仅仅是密钥扩展不同，即扩展原始密钥的应用，然后将其应用于除第一轮和最后一轮之外的所有轮密钥。这被称为直接解密算法解密算法D。在此算法中，仅步骤与加密本身不同，但步骤的顺序并未以相同方式出现，以便

差分和线性密码分析的诞生为迭代分组密码设计奠定了理论基础。目前，对于一个新的分组密码，只有在提供了能够抵御差分和线性分析的证据之后，才可能被认真考虑。当然，差分和线性分析不仅可用于攻击。一个分组密码应当能够抵抗各种可预见的密码分析。然而，在大多数情况下，抵御差分和线性分析已成为分组密码的主要评判标准，而其他已知的攻击手段则作为次要考虑因素，通常只需对原始设计进行轻微修改即可抵御。

4. 实验与分析

A. 密钥敏感性分析

通过敏感性分析计算密钥，仅采用不同的初始值、不同的控制参数和不同的迭代值。不同的密钥值 $ x_2 = 0.003600660015037 $，$ \mu_2 = 3.90153455419664 $，$ N_2 = 3001 $。结果如图4所示。

对50幅不同内容的数字彩色图像使用不同的密钥组进行了两类数据的密钥敏感性分析，分析结果如图4和图5所示。与上述两图类似的数据结果客观真实。可以看出，加密算法通过密钥敏感性分析得到的相关系数是极小甚至为负，这表明本文提出的加密算法对密钥极为敏感，安全性高，是一种优秀的加密算法。

B. 安全分析

标准批次的安全分析，本节主要进行以下安全分析项目：密钥空间分析、减法密集速度分析、直方图分析、明文密文相关性分析、密钥敏感性分析、相邻像素相关性分析、差分攻击。

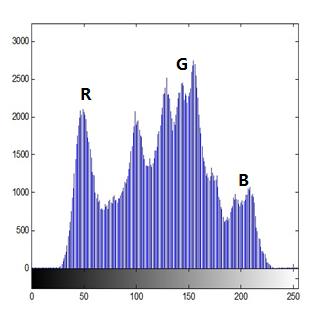
如果目标图像是彩色图像，由于彩色图像具有红、绿、蓝三个通道分量，因此需要为该彩色图像分别绘制红、绿、蓝三个通道的三幅直方图。公式如下：

$$
p’(z) = \frac{1}{D_{R,G,B}} \int\int_{(x,y)\in R,G,B} p(z|x,y) \, dx\,dy \tag{10}
$$

红、绿、蓝代表彩色图像的红色、绿色和蓝色通道。对于一个良好的图像加密算法，加密图像直方图是平滑的，可进行统计分析而不绘制加密图像的像素分布。因此，要加密的彩色图像必须满足加密后的彩色图像直方图三个通道均平滑。利用上述公式，我们可以绘制出原始图像和加密lena图像的直方图，如图6所示：

绘制了20组不同密钥下20种不同内容的数字彩色图表加密后的直方图，绘制结果与图7完全一致，所有加密密文的分布直方图均平滑。明文lena和密文lena图像之间的相关系数如表1所示。

表1. 明文和密文Lena图像之间的相关系数

明文/密文	Red 通道	Blue 通道	绿色 通道
红色通道	0.0078	-0.0015	-0.0016
蓝色通道	0.008	-0.002	-0.003
绿色通道	0.007	-0.003	0.002

使用本文所述数字加密算法对内容完全不同的彩色图像进行加密，采用50组不同的密钥，得到9个密文图像的相关系数。从50组数据的相关系数表中可以看出，每组相关系数的数值都非常小，可以说接近于零，因此可以得出结论：本文所使用的加密算法对数字彩色图像进行加密后得到的密文图像几乎是随机的图像。

5. 结论

随着互联网技术和数字多媒体技术的快速发展，公众可以快速获取各种数字多媒体信息图像，网络上的视频传输涉及个人、企业、医疗机构、军事、国家等主体，这些主体都希望图像信息在存储和传输过程中安全可靠，不受威胁，对信息完整性、图像传输时间、隐私性和可靠性提出了更高的要求。本文通过仿真实验表明，该算法能够在加解密算法速度与安全性之间取得良好平衡，具有高安全性以及快速的加密算法加解密速度，适用于实时视频通信和安全通信，并提出了两种基于混沌映射的彩色图像加密算法进行对比与性能分析。