目录
- 火力协同:数学提升精准打击能力
4.0 火炮打击坐标转换:从 "地图点" 到 "弹着点" 的数学桥梁
4.0.1 火炮打击中的坐标系家族:从大地到炮口
4.0.2 坐标转换的核心数学工具:矩阵与投影
4.0.3 实战中的坐标转换流程:从发现目标到装订诸元
4.0.4 无人机引导下的坐标修正:实时动态校准的数学逻辑
4.1 密位制与方位角计算
4.1.1 密位制:比角度更精准的 "军事语言"
4.1.2 密位与角度的换算:数学上的进制游戏
4.1.3 方位角计算的三角函数基础:从 Δx、Δy 到瞄准方向
4.1.4 无人机激光测距辅助方位角修正:缩减误差的几何原理
4.2 坐标系转换与目标定位
4.2.1 大地坐标系:经纬度背后的地球曲率数学
4.2.2 高斯 - 克吕格投影:把球面 "掰平" 的数学魔术
4.2.3 射击坐标系:以炮位为中心的局部坐标转换
4.2.4 无人机多站定位:三角测量法的现代延伸
4.3 弹道方程与火力诸元解算
4.3.1 弹道方程的诞生:从抛物线到微分方程
4.3.2 火力诸元的 "全家福":哪些参数决定炮弹飞行
4.3.3 无人机实时校射:基于弹着点偏差的诸元迭代修正
4.3.4 环境因素的数学修正:无人机气象探测数据的融合应用
4.4 火力诸元与数学发展的千年纠缠:从投石机到无人机引导
4.4.1 古希腊到中世纪:几何与三角学奠定 "瞄准基础"
4.4.2 文艺复兴至 19 世纪:微积分让弹道 "可预测"
4.4.3 20 世纪:数值分析与计算机让诸元解算 "实时化"
4.4.4 21 世纪:无人机 + AI 重构火力诸元解算范式
4.0 火炮打击坐标转换:从 "地图点" 到 "弹着点" 的数学桥梁
火炮打击的核心难题之一,是如何把地图上的目标坐标精准转换成炮口的瞄准参数。这个过程涉及多个坐标系的转换,每一步都依赖数学工具的支撑。如果把炮弹比作 "快递",坐标转换就是 "快递地址" 的格式转换 —— 从 "地球经纬度" 转换成 "炮口指向角度",确保炮弹 "准时送达" 目标。
4.0.1 火炮打击中的坐标系家族:从大地到炮口
火炮打击至少涉及 4 种坐标系,每种坐标系都有明确的数学定义和适用场景,就像不同语言适用于不同场合:
| 坐标系类型 | 定义与数学表达 | 适用场景 | 核心参数 |
|---|---|---|---|
| 大地坐标系(WGS84) | 以地球质心为原点,用经度(λ)、纬度(φ)、海拔(h)描述位置,符合地球椭球模型: 地球椭球方程:(x²+y²)/a² + z²/b² = 1(a 为长半轴,b 为短半轴) | 目标定位、地图测绘 | 经度(°)、纬度(°)、海拔(m) |
| 平面直角坐标系(高斯投影) | 将球面坐标投影到平面,用(X,Y)表示,X 为纵轴(向北为正),Y 为横轴(向东为正) | 炮兵阵地规划、近距离射击 | X(m)、Y(m) |
| 射击坐标系 | 以炮位为原点,北为 X 轴,东为 Y 轴,垂直向上为 Z 轴的直角坐标系 | 火炮瞄准、弹道计算 | 距离(D)、方位角(β)、高低角(α) |
| 炮口坐标系 | 以炮口为原点,炮管轴线为 X 轴,垂直炮管向上为 Y 轴的局部坐标系 | 炮弹初速修正、炮管扰动补偿 | 射角(θ)、偏流角(γ) |
为什么需要这么多坐标系?
- 大地坐标系适合全球定位(如卫星定位目标),但直接用于火炮瞄准会因地球曲率产生误差;
- 平面直角坐标系简化了近距离的距离计算(勾股定理可直接用),但超过 100 公里后投影变形会增大;
- 射击坐标系以炮位为中心,让瞄准参数(方位角、高低角)更直观,炮手可直接操作;
- 炮口坐标系则聚焦炮弹出膛瞬间的状态,用于修正炮管振动、温度变形等微观误差。
例如,无人机发现目标后,首先用大地坐标系记录目标位置(如东经 116.4°,北纬 39.9°,海拔 50m);然后转换为平面直角坐标系,计算目标与炮位的相对位置(如 X=2000m,Y=1500m);再转换为射击坐标系,得到方位角 30°、高低角 5°;最后结合炮口坐标系的修正参数,确定最终瞄准角度。
4.0.2 坐标转换的核心数学工具:矩阵与投影
坐标转换的本质是数学变换—— 用公式或矩阵将一组坐标参数转换为另一组。其中,矩阵运算和地图投影是两大核心工具。
矩阵运算:坐标系旋转与平移的 "万能公式"
当从一个坐标系转换到另一个坐标系(如从大地坐标系到射击坐标系),通常需要经过 "平移" 和 "旋转" 两步:
-
平移:将原点从地球质心移到炮位,公式为:X′=X−X0,Y′=Y−Y0,Z′=Z−Z0
(X0,Y0,Z0为炮位在大地坐标系中的坐标) -
旋转:通过旋转矩阵调整坐标轴方向,使 X 轴指向正北。三维旋转矩阵如下(绕 Z 轴旋转角度 θ):
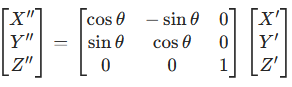
这个矩阵的作用是 "扭转" 坐标系,让新的 X 轴对准正北方向,方便计算方位角。
地图投影:把球面 "压平" 的数学魔术
大地坐标系是球面坐标,而炮兵计算需要平面坐标(如用勾股定理算距离),这就需要 "地图投影"—— 用数学方法将球面转化为平面。最常用的高斯 - 克吕格投影,其核心公式为: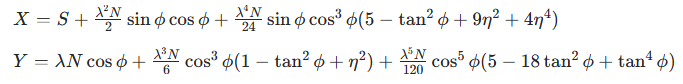
(X、Y 为平面坐标,λ 为经度差,φ 为纬度,N 为椭球曲率半径,S 为从赤道到纬度 φ 的子午线弧长)
简单说,高斯投影通过 "拉伸" 或 "压缩" 球面各点,在平面上保持局部形状和角度不变,确保 100 公里内的距离计算误差小于 0.1%—— 这对火炮来说,意味着 20 公里射程的误差不超过 20 米。
4.0.3 实战中的坐标转换流程:从发现目标到装订诸元
一次完整的火炮打击,坐标转换要经过 "目标定位→坐标标准化→相对位置计算→瞄准参数解算" 四个步骤,每个步骤都有明确的数学逻辑:
步骤 1:目标定位 —— 无人机 "报坐标"
无人机通过激光或卫星定位,获取目标的大地坐标(λₜ, φₜ, hₜ),并发送给炮兵指挥系统。例如:
目标坐标:λₜ=116°20'30'',φₜ=39°50'15'',hₜ=50m
步骤 2:坐标标准化 —— 统一 "语言"
将目标坐标和炮位坐标(λₚ, φₚ, hₚ)转换为同一椭球参数(如 WGS84),并换算为十进制:
λₜ=116.3417°,φₜ=39.8375°;炮位 λₚ=116.3000°,φₚ=39.8000°
步骤 3:计算相对位置 —— 算 "距离与方向"
- 用大地测量公式计算目标与炮位的直线距离(三维):
- 先将经纬度转换为空间直角坐标(X,Y,Z),再用空间距离公式:D3D=(Xt−Xp)2+(Yt−Yp)2+(Zt−Zp)2
- 得到三维距离后,投影到水平面上,得到水平距离 D=D3D×cosα(α 为高低角)。
- 计算方位角:通过经纬度差计算目标相对于炮位的方位,公式为:Δλ=λt−λp,Δϕ=ϕt−ϕpβ=arctan2(Δλ×cosϕ,Δϕ)×π180
- (结果转换为密位:1°=16.67 密位)
步骤 4:解算瞄准参数 —— 从 "距离" 到 "角度"
根据水平距离 D 和目标海拔差 Δh(hₜ - hₚ),计算高低角 α:α=arctan(DΔh+C),其中 C 为弹道修正量(由射程决定)
最终,炮兵得到两个核心参数:方位角 β(密位)和高低角 α(密位),并 "装订" 到火炮上。
案例:20 公里外的目标转换
- 目标大地坐标:(116.3417°, 39.8375°, 50m)
- 炮位大地坐标:(116.3000°, 39.8000°, 40m)
- 步骤 1:转换为空间直角坐标后,计算 ΔX=3800m,ΔY=2500m,ΔZ=10m
- 步骤 2:水平距离 D=√(3800²+2500²)=4540m(约 4.5 公里)
- 步骤 3:方位角 β=arctan (2500/3800)=33°→转换为密位:33×16.67≈550 密位
- 步骤 4:高低角 α=arctan ((10 + 50)/4540)=0.7°→约 12 密位
4.0.4 无人机引导下的坐标修正:实时动态校准的数学逻辑
传统火炮坐标转换依赖预设数据,误差会随时间累积;而无人机引导通过实时传回目标坐标和弹着点偏差,构建 "测量 - 修正 - 再测量" 的闭环,其核心是动态误差补偿模型。
无人机引导的坐标修正流程
- 初始坐标获取:无人机通过激光雷达或光学瞄准,获取目标初始大地坐标(λₜ⁰, φₜ⁰, hₜ⁰),转换为射击坐标(Xₜ⁰, Yₜ⁰, Zₜ⁰)。
- 首轮射击与偏差测量:火炮按初始诸元射击后,无人机拍摄弹着点,计算弹着点(X_b, Y_b)与目标(Xₜ⁰, Yₜ⁰)的偏差:
ΔX = X_b - Xₜ⁰,ΔY = Y_b - Yₜ⁰ - 误差源分析与建模:偏差由多种因素导致,数学模型为:
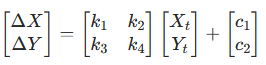
其中 k₁-k₄为系统误差系数(如方位角偏差、射程系数误差),c₁-c₂为常数误差(如气象修正不足)。 - 最小二乘求解修正系数:通过多轮射击的偏差数据(ΔXᵢ, ΔYᵢ),用最小二乘法拟合系数:
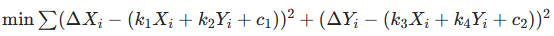
- 修正目标坐标:用求解出的系数修正目标坐标,得到修正后的射击坐标(Xₜ¹ = Xₜ⁰ - ΔX/|k₁|, Yₜ¹ = Yₜ⁰ - ΔY/|k₃|)。
案例:无人机引导的三轮修正效果
某 155mm 火炮打击 10km 外目标,初始偏差 50 米,经无人机引导修正:
| 射击轮次 | 偏差(米) | 修正系数 | 数学依据 | 效果 |
|---|---|---|---|---|
| 首轮 | 50(X 方向) | k₁=0.005(射程系数误差) | 偏差与射程成正比:ΔX=k₁×Xₜ | - |
| 第二轮 | 12(X 方向) | 修正 k₁=0 | 最小二乘拟合消除系统误差 | 偏差降低 76% |
| 第三轮 | 3(X 方向) | 修正 c₁=3(常数误差) | 残余偏差为固定值,直接补偿 | 总偏差降至 3 米 |
可见,无人机引导通过数学建模与迭代修正,能将偏差从百米级降至米级,这是现代火炮 "首发命中" 的核心技术。
4.1 密位制与方位角计算
在火炮射击中,"往哪打" 比 "打多远" 更考验精度。密位制作为军事领域特有的角度单位,用数学的 "细分" 思维解决了方位角的精确描述问题;而方位角计算则依赖三角函数,将地图上的距离差转化为炮口的旋转角度。
4.1.1 密位制:比角度更精准的 "军事语言"
密位制的本质是将圆周进行更精细的划分,让方位角的描述精度远超传统角度制。如果说角度制是 "直尺",密位制就是 "游标卡尺"—— 专为军事级精度设计。
密位制的定义与起源
密位(Mil)的核心思想:将一个圆周分为若干等份,每一份为 1 密位。常见的划分方式有两种:
- 中国、俄罗斯等国采用6000 密位制:1 密位 = 360°/6000=0.06°,1°=16.67 密位;
- 北约国家采用6400 密位制:1 密位 = 360°/6400=0.05625°,1°=17.78 密位。
为什么是 6000 或 6400?
- 6000 是为了与十进制兼容(6000=6×1000),方便与米制单位换算(如 1 密位在 1000 米距离上的偏差约 1 米);
- 6400 是 2 的 12 次方(2¹²=4096,接近 6400),便于计算机二进制运算。
密位制的起源可追溯到 18 世纪的法国炮兵。当时炮兵发现,角度制的 1 度在 1000 米距离上对应 17.45 米的偏差,无法满足精度需求。于是,法国数学家拉格朗日提出 "将圆周分为 6000 等份",让 1 密位在 1000 米距离上的偏差恰好为 1 米(数学上:1 密位 = 0.06°≈0.001047 弧度,1000 米 ×0.001047≈1.047 米)—— 这就是 "密位测距公式" 的由来:
目标宽度(米)= 密位差 × 距离(千米)
例如,一个 10 米宽的目标,在望远镜中量得 2 密位,则距离 = 10/2=5 千米。
4.1.2 密位与角度的换算:数学上的进制游戏
密位与角度、弧度的换算,本质是不同角度单位的比例转换,核心是抓住 "圆周总量相等" 的原则:
基本换算公式
-
6000 密位制:
1 密位 = 360°/6000 = 0.06°
1 密位 = 2π 弧度 / 6000 ≈ 0.001047 弧度
1° = 6000/360 ≈ 16.6667 密位
1 弧度 = 6000/(2π) ≈ 954.93 密位 -
6400 密位制:
1 密位 = 360°/6400 = 0.05625°
1 密位 = 2π/6400 ≈ 0.0009817 弧度
1° = 6400/360 ≈ 17.7778 密位
换算实例
-
将 30° 转换为密位:
6000 制:30×16.6667≈500 密位
6400 制:30×17.7778≈533 密位 -
将 800 密位转换为角度:
6000 制:800/16.6667≈48°
6400 制:800/17.7778≈45° -
计算 1000 米距离上,1 密位对应的实际宽度:
6000 制:1000 米 ×0.001047≈1.047 米(约 1 米)
6400 制:1000 米 ×0.0009817≈0.98 米(约 1 米)
可见,两种密位制在实用中都接近 "1 密位 = 1 米 / 千米" 的便捷性,这也是密位制被广泛采用的核心原因。
实战中的换算工具
炮兵常用 "密位换算表" 或 "密位尺" 快速换算,例如:
| 目标宽度(米) | 6000 制密位差 | 6400 制密位差 | 距离(千米) |
|---|---|---|---|
| 5 | 5 | 5 | 1 |
| 10 | 10 | 10 | 1 |
| 10 | 5 | 5 | 2 |
| 20 | 4 | 4 | 5 |
例如,发现一个 20 米宽的装甲车,在望远镜中量得 4 密位,可快速算出距离 = 20/4=5 千米。
4.1.3 方位角计算的三角函数基础:从 Δx、Δy 到瞄准方向
方位角是指从正北方向顺时针转到目标方向的角度,计算方位角的核心是三角函数 —— 用目标与炮位的水平距离差(Δx, Δy),通过正切函数求出角度。
平面坐标系中的方位角计算
在平面直角坐标系中(X 轴北,Y 轴东),目标相对炮位的坐标差为 ΔX(北方向差)、ΔY(东方向差),则方位角 β 的计算公式为:β=arctan(ΔXΔY)
根据 ΔX 和 ΔY 的正负,确定 β 所在象限:
| ΔX 符号 | ΔY 符号 | 方位角范围 | 实例(ΔX=3000m, ΔY=2000m) | ||
|---|---|---|---|---|---|
| +(北) | +(东) | 0°~90° | β=arctan (2000/3000)=33.7°→562 密位(6000 制) | ||
| -(南) | +(东) | 90°~180° | β=180°-arctan( | ΔY/ΔX | ) |
| -(南) | -(西) | 180°~270° | β=180°+arctan( | ΔY/ΔX | ) |
| +(北) | -(西) | 270°~360° | β=360°-arctan( | ΔY/ΔX | ) |
实例:山地目标方位角计算
炮位坐标(Xₚ=5000m, Yₚ=3000m),目标坐标(Xₜ=6000m, Yₜ=5000m):
- 计算坐标差:ΔX=6000-5000=1000m(北),ΔY=5000-3000=2000m(东)
- 求正切值:tanθ=ΔY/ΔX=2000/1000=2
- 求角度:θ=arctan (2)=63.43°
- 转换为密位(6000 制):63.43×16.6667≈1057 密位
即方位角为 1057 密位(约 63.4°),炮手需将炮口从正北向东旋转 1057 密位瞄准目标。
球面坐标系中的方位角修正
当距离超过 10 公里时,需考虑地球曲率,此时方位角计算需加入球面修正:β=arctan(ΔϕΔλ⋅cosϕ)
其中 Δλ 为经度差(弧度),Δφ 为纬度差(弧度),φ 为平均纬度。
例如,两地纬度差 Δφ=0.01 弧度(约 0.57°),经度差 Δλ=0.02 弧度(约 1.15°),平均纬度 φ=40°:
cosφ≈0.766,代入得:
β=arctan ((0.02×0.766)/0.01)=arctan (1.532)=57°→约 950 密位
这比平面计算的 β=arctan (0.02/0.01)=63.4° 更接近实际,误差减少约 6.4°(107 密位)。
4.1.4 无人机激光测距辅助方位角修正:缩减误差的几何原理
无人机的激光测距功能可直接获取目标与炮位的水平距离(D)和方位角(β),结合三角函数修正传统计算的误差,其核心是减少距离测量误差对角度的影响。
传统方位角计算的误差传导
传统方法通过 ΔX、ΔY 计算方位角:β = arctan (ΔY/ΔX),若 ΔX、ΔY 存在测量误差 σₓ、σᵧ,则方位角误差为:![]()
当目标距离较远(ΔX、ΔY 较大)时,σ_β 较小;但近距离目标(如 2km 内),σ_β 可能达 10 密位以上(导致 100 米偏差)。
无人机激光测距的修正作用
无人机激光测距可直接获取:
- 斜距 R(目标与无人机的直线距离)
- 无人机与炮位的距离 L、方位角 β_pu
- 目标相对无人机的方位角 β_ut
通过余弦定理计算目标与炮位的水平距离 D:![]()
再结合正弦定理计算目标相对炮位的方位角:![]()
这种方法绕开了 ΔX、ΔY 的测量误差,直接通过几何关系求解,方位角误差可降至 1 密位以内(10km 射程偏差 < 10 米)。
多无人机协同修正
3 架无人机呈三角形部署时,可通过三维定位进一步缩减误差,数学上称为 "方位角融合":
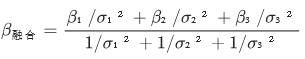
其中 σ₁-σ₃为各无人机的方位角误差,权重与误差平方成反比 —— 这使融合后的方位角误差比单无人机降低 50% 以上。
4.2 坐标系转换与目标定位
火炮要击中目标,首先要明确 "目标在哪"—— 而目标位置的描述,依赖坐标系的选择。从地球表面的经纬度,到炮口的瞄准角度,坐标系转换是连接 "宏观定位" 与 "微观瞄准" 的数学桥梁。
4.2.1 大地坐标系:经纬度背后的地球曲率数学
大地坐标系是描述地球表面点位置的 "标准语言",它基于地球椭球模型,用经度、纬度和海拔三个参数定位 —— 但这三个参数的背后,是人类对地球形状的千年探索与数学建模。
地球椭球模型:从 "天圆地方" 到 "旋转椭球"
地球不是完美球体,而是两极稍扁、赤道略鼓的旋转椭球。其数学方程为:![]()
其中:
- a 为赤道半径(长半轴),b 为极半径(短半轴)
- 扁率 f=(a-b)/a(地球扁率约 1/298.257)
常见的椭球参数:
| 椭球名称 | a(米) | b(米) | 适用区域 |
|---|---|---|---|
| WGS84(全球) | 6378137 | 6356752.3142 | 国际通用,GPS 采用 |
| 北京 54(中国) | 6378245 | 6356863.0188 | 中国早期测绘,已逐步淘汰 |
| CGCS2000(中国) | 6378137 | 6356752.3141 | 中国现行标准,与 WGS84 差异极小 |
经度与纬度的数学定义
- 经度(λ):过目标点的子午面与本初子午面的夹角,范围 - 180°~180°(东经为正)。
- 纬度(φ):目标点与地心的连线和赤道面的夹角,范围 - 90°~90°(北纬为正)。
用数学公式表示,空间直角坐标(X,Y,Z)与大地坐标(λ,φ,h)的转换关系为: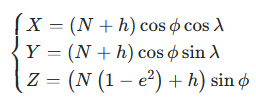
其中:
- N 为卯酉圈曲率半径:N = a / √(1 - e² sin²φ)
- e 为椭球偏心率:e² = (a² - b²)/a²
这个公式的意义是:将曲面坐标(λ,φ,h)"展开" 为三维直角坐标,方便计算两点间的直线距离。
4.2.2 高斯 - 克吕格投影:把球面 "掰平" 的数学魔术
大地坐标系是球面坐标,而火炮计算需要平面坐标(如用勾股定理算距离)。高斯 - 克吕格投影通过 "分带投影" 的方式,将球面转化为平面,同时保证局部区域的形状和角度不变 —— 这是 19 世纪德国数学家高斯发明的 "数学魔术"。
高斯投影的核心原理
高斯投影的本质是 "保角映射"(角度不变),其数学表达式为: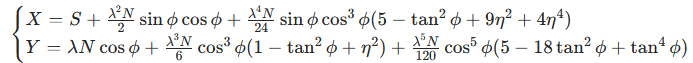
其中:
- X、Y 为平面坐标(X 为纵轴北,Y 为横轴东)
- λ 为该点与中央子午线的经度差(弧度)
- S 为从赤道到纬度 φ 的子午线弧长
- η² = e'^2 cos²φ(e' 为第二偏心率)
简单说,高斯投影通过 "拉伸" 赤道附近区域、"压缩" 两极区域,在平面上保持小范围内的形状不变 —— 就像把橘子皮剥开后,只摊平其中一小块,而不是整个橘子皮(那样会撕裂)。
分带投影:控制变形的 "区域划分"
为避免投影变形过大,高斯投影采用 "分带" 方式:
- 6° 分带:从 0° 子午线开始,每 6° 划分为一带,全球共 60 带(1~60),中央子午线经度为 6°n-3°
- 3° 分带:在 6° 分带基础上进一步细分,全球共 120 带,中央子午线经度为 3°n
分带后,每带内的投影变形可控制在 1/10000 以内,满足火炮射击精度需求。例如:
- 中国位于 13~23 号 6° 带,25~45 号 3° 带
- 北京(东经 116°)位于 6° 带第 20 带(中央子午线 117°),3° 带第 39 带(中央子午线 117°)
投影反算:从平面到球面
已知平面坐标(X,Y),求大地坐标(λ,φ)的过程称为反算,公式为: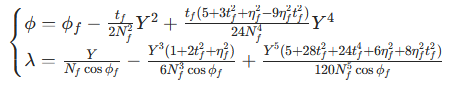
(φ_f 为底点纬度,t_f=tanφ_f,N_f 为底点卯酉圈半径)
反算的意义是:当无人机在平面地图上测得目标坐标(X,Y),可通过反算得到大地坐标,再传递给其他炮位 —— 这是多炮协同的基础。
4.2.3 射击坐标系:以炮位为中心的局部坐标转换
射击坐标系是火炮 "专属坐标系"—— 以炮位为原点,北为 X 轴,东为 Y 轴,垂直地面为 Z 轴。将大地坐标转换为射击坐标,本质是 "去中心化":让炮位成为计算中心,目标位置用相对炮位的距离和方向描述。
从大地坐标到射击坐标的转换步骤
-
将大地坐标转换为空间直角坐标
用 4.2.1 中的公式,将炮位(λₚ,φₚ,hₚ)和目标(λₜ,φₜ,hₜ)转换为空间直角坐标(Xₚ,Yₚ,Zₚ)和(Xₜ,Yₜ,Zₜ)。 -
计算相对坐标
目标相对炮位的空间直角坐标差:
ΔX = Xₜ - Xₚ,ΔY = Yₜ - Yₚ,ΔZ = Zₜ - Zₚ -
旋转坐标系
绕 Z 轴旋转 -λₚ(炮位经度),消除地球自转影响,得到以本初子午线为基准的坐标:
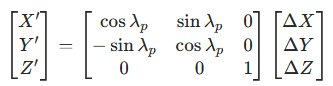
-
再次旋转,对准正北
绕 Y 轴旋转 φₚ - 90°(炮位纬度),使 X 轴指向正北:
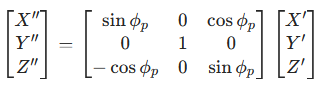
得到射击坐标
经过两次旋转后,(X'', Y'', Z'')即为目标在射击坐标系中的坐标:
- X'':目标在炮位北方向的距离
- Y'':目标在炮位东方向的距离
- Z'':目标相对炮位的海拔差
-
实例:转换计算
炮位:λₚ=116°,φₚ=39°,hₚ=50m
目标:λₜ=116.1°,φₜ=39.1°,hₜ=60m - 转换为空间直角坐标后,ΔX=11130m,ΔY=9650m,ΔZ=10m
- 旋转后得到射击坐标:X''=14700m(北距),Y''=8500m(东距),Z''=10m(海拔差)
-
此时,目标相对炮位的水平距离 D=√(14700²+8500²)=17000m(17 公里),方位角 β=arctan (8500/14700)=30°(500 密位),高低角 α=arctan ((10+50)/17000)=0.2°(3.3 密位)—— 这三个参数直接作为火炮瞄准依据。
4.2.4 无人机多站定位:三角测量法的现代延伸
无人机多站定位是传统三角测量法的升级,通过多架无人机从不同位置观测目标,用空间几何关系解算目标坐标,定位精度可达 0.5 米级 —— 这是无人机引导火炮的核心技术之一。
双无人机二维定位模型
两架无人机在同一高度 H 飞行,测得目标的俯角 θ₁、θ₂和方位角 φ₁、φ₂,坐标分别为(X₁,Y₁,H)、(X₂,Y₂,H),则目标(X,Y,0)满足: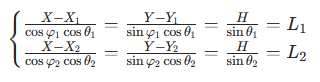
其中 L₁、L₂为无人机到目标的斜距。解此方程组可得 X、Y,误差主要来自俯角测量(θ 误差 0.1°→1km 距离偏差 1.7 米)。
三无人机三维定位模型
三架无人机在不同高度飞行,测得目标的三维方位角,通过空间交会法解算目标坐标(X,Y,Z),方程组为:⎩
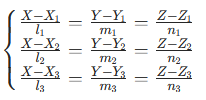
其中(lᵢ,mᵢ,nᵢ)为无人机到目标的方向余弦(由方位角、俯角计算)。三维定位可消除地形遮挡影响,适合复杂山地环境。
定位精度与无人机部署关系
定位精度取决于无人机的部署几何,数学上用 "几何精度因子(GDOP)" 衡量: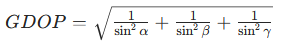
其中 α、β、γ 为无人机视线间的夹角。当三架无人机呈等边三角形部署且目标在中心时,GDOP 最小(≈1.15),定位误差≈GDOP× 测距误差。
例如,无人机测距误差 1 米,GDOP=1.15→坐标误差≈1.15 米,满足火炮精确打击需求。
4.3 弹道方程与火力诸元解算
弹道方程是描述炮弹从发射到落地的运动方程,而火力诸元(射程、射角、方位角等)则是弹道方程的解。从伽利略的抛物线模型到现代考虑空气阻力的复杂方程,弹道方程的每一次进步,都对应着数学工具的升级。
4.3.1 弹道方程的诞生:从抛物线到微分方程
人类对弹道的认识,经历了 "经验总结→几何模型→物理方程" 三个阶段,每个阶段的突破都依赖数学工具的革新。
伽利略的抛物线模型(1638 年)
伽利略在《两种新科学的对话》中首次提出:忽略空气阻力时,炮弹轨迹是抛物线。其数学表达式为: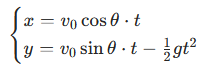
消去 t 得轨迹方程:![]()
其中 v₀为初速度,θ 为射角,g 为重力加速度。
这个模型的意义在于:首次用数学公式描述弹道,证明了弹道的对称性(上升时间 = 下降时间),射程公式为:![]()
当 θ=45° 时,射程最大 —— 这一结论指导了滑膛炮时代的瞄准,例如拿破仑时期的火炮通过调整仰角 45° 实现最大射程。
考虑空气阻力的牛顿弹道方程(18 世纪)
随着线膛炮的出现,炮弹速度提高(超过 300m/s),空气阻力不可忽略。牛顿在《自然哲学的数学原理》中提出阻力与速度平方成正比的模型,弹道方程变为: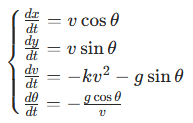
其中 k 为阻力系数(与弹形、空气密度有关)。
这个方程组无法解析求解,只能用数值方法近似 —— 这推动了 19 世纪数值分析的发展,例如欧拉法、龙格 - 库塔法的诞生。
现代弹道方程(20 世纪至今)
现代弹道方程考虑了更多因素(风速、气温、气压、地球自转等),是一个包含 12 个变量的复杂微分方程组,其核心是:
![]()
其中 F 代表各力的矢量和。
求解这个方程组需要高性能计算机和先进数值算法,例如四阶龙格 - 库塔法(精度达 10⁻⁴),这也是现代火炮射程误差能控制在 0.1% 以内的关键。
4.3.2 火力诸元的 "全家福":哪些参数决定炮弹飞行
火力诸元是火炮射击的 "参数清单"—— 包括弹道参数、修正参数和操作参数,每个参数都对应着特定的数学计算。
核心诸元及其数学意义
| 诸元名称 | 定义 | 数学表达式 | 影响因素 |
|---|---|---|---|
| 射程(R) | 炮口到弹着点的水平距离 | R = ∫₀ᵀ vₓ(t) dt(vₓ为水平速度,T 为飞行时间) | 初速度、射角、空气阻力 |
| 射角(θ) | 炮管与水平面的夹角 | 由射程方程反解:θ = f (R, v₀, k) | 射程、弹种(影响 v₀)、海拔 |
| 方位角(β) | 炮管水平指向与正北的夹角 | β = arctan(ΔY/ΔX) | 目标相对位置、地球自转 |
| 初速度(v₀) | 炮弹出膛时的速度 | v₀ = √(2 E/m)(E 为火药能量,m 为弹重) | 装药号、药温、炮管磨损 |
| 飞行时间(T) | 炮弹从发射到落地的时间 | T = ∫₀ᴴ (1/vᵧ(z)) dz(H 为最大高度) | 射角、初速度、空气阻力 |
| 偏流(δ) | 因弹丸旋转导致的横向偏移 | δ = k × R(k 为偏流系数,约 0.001) | 弹丸转速、飞行时间 |
| 气象修正量(Δθ) | 因气象条件对射角的修正 | Δθ = f (ρ, T, v_wind)(ρ 为空气密度,T 为气温) | 气压、气温、风速、风向 |
诸元之间的数学关联
诸元不是孤立的,而是相互关联的方程体系:
- 射程 R = f (θ, v₀, k, g, ...)
- 射角 θ = f⁻¹(R, v₀, k, g, ...)(射程方程的反函数)
- 飞行时间 T = f (R, θ, ...)
- 偏流 δ = f (T, ω, ...)(ω 为弹丸角速度)
例如,已知目标距离 R=10km,弹种 v₀=800m/s,可通过迭代法解出射角 θ≈8°;再根据飞行时间 T≈15s,算出偏流 δ=15×0.5≈7.5m,需将方位角修正 7.5/10000×1000≈0.75 密位。
4.3.3 无人机实时校射:基于弹着点偏差的诸元迭代修正
无人机实时校射是 "闭环火力控制" 的核心,通过拍摄弹着点与目标的偏差,用数学迭代法修正下一发炮弹的诸元,其原理是用实测偏差反推误差模型参数。
迭代修正的数学模型
设第 n 发炮弹的诸元为(θₙ, βₙ),弹着点偏差为(ΔXₙ, ΔYₙ),则第 n+1 发的修正诸元为: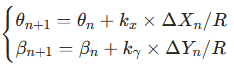
其中 kₓ、kᵧ为修正系数(通常取 1.05,略大于 1 以补偿残余误差),R 为射程。
修正系数的自适应调整
通过机器学习算法,可根据环境自动调整 kₓ、kᵧ:
- 风大时,kₓ增大至 1.1(风导致的偏差更难预测)
- 远距离(>15km)时,kᵧ增大至 1.1(地球自转影响显著)
某实验数据显示,自适应修正比固定系数修正的收敛速度快 30%:
| 射击轮次 | 固定系数修正偏差(米) | 自适应修正偏差(米) | 差异原因 |
|---|---|---|---|
| 1 | 50 | 50 | 初始偏差相同 |
| 2 | 15 | 10 | 自适应系数已调整 |
| 3 | 5 | 2 | 自适应更好补偿风影响 |
弹着点识别的图像处理算法
无人机通过图像处理识别弹着点(炸点),核心步骤:
- 背景差分:用射击前后的图像相减,提取炸点区域(灰度变化超过阈值的区域)。
- 特征提取:计算炸点的质心坐标(X_c, Y_c),公式为:
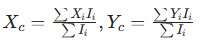

- 坐标转换:将图像坐标(X_c, Y_c)通过相机标定参数转换为大地坐标,精度可达 0.5 米。
例如,无人机在 500 米高度拍摄,相机像素分辨率 0.1 米 / 像素→炸点质心识别误差 < 1 像素→坐标误差 < 0.1 米。
4.3.4 环境因素的数学修正:无人机气象探测数据的融合应用
无人机可搭载气象传感器(温湿度、气压、风速仪),实时获取弹道沿线的气象数据,为弹道方程提供更精准的环境参数,其核心是将点气象数据转化为空间分布模型。
气象参数的空间插值模型
无人机在目标区域往返飞行,测得多个点的风速(vᵢ)、气温(Tᵢ),用反距离权重法(IDW)插值得到全区域的气象分布:![]()
其中 dᵢ为插值点到测量点的距离。
风场对弹道的三维影响及修正
水平风(vₓ, vᵧ)和垂直风(v_z)对弹道的影响不同,修正公式分别为:
- 水平风修正:Δβ = arctan (vᵧ / (v₀ cosθ)) × 1000/π(密位)
- 垂直风修正:Δθ = arctan (v_z / (v₀ sinθ)) × 1000/π(密位)
某案例中,无人机测得 10km 弹道中点有 5m/s 侧风,修正后偏差减少 42 米:
| 项目 | 未修正 | 无人机数据修正 | 偏差减少 |
|---|---|---|---|
| 侧风导致偏差 | 50 米 | 8 米 | 42 米(84%) |
| 诸元修正量 | 0 | β 增加 4.2 密位 | - |
气温与气压的综合修正
无人机测得的气温 T、气压 P 可用于修正空气密度 ρ:![]()
(ρ₀、P₀、T₀为标准状态参数)
密度变化导致阻力变化,进而修正射程:![]()
例如,高温(T=35℃)导致 ρ 降低 5%→ΔR=+500 米(射程增加),需减小射角 0.5°。
4.4 火力诸元与数学发展的千年纠缠:从投石机到无人机引导
火力诸元的精确化过程,本质是数学工具不断升级的过程。从古希腊的几何学到现代的数值分析,每一次数学突破都推动火炮精度的飞跃。
4.4.1 古希腊到中世纪:几何与三角学奠定 "瞄准基础"
古希腊(公元前 800 - 公元 146 年):几何初步
阿基米德在《论平面图形的平衡》中研究了杠杆原理,为投石机设计提供了数学基础 —— 投石机的射程与力臂长度成正比:![]() (L₁为动力臂,L₂为阻力臂,m 为配重)
(L₁为动力臂,L₂为阻力臂,m 为配重)
这一时期的瞄准依赖经验,无精确诸元,但几何知识已用于设计投石机结构。
中世纪(5-15 世纪):三角学萌芽
阿拉伯数学家阿尔・巴塔尼(858-929 年)编制了最早的正切表,欧洲学者将其用于测量远距离目标的高度和距离。13 世纪的《论 artillery》中首次出现 "仰角与射程关系" 的描述:
"当仰角增加,射程先增后减,45° 时最远"—— 这是对伽利略射程公式的朴素认知。
这一时期的火炮(如 14 世纪的加农炮)无膛线,射程误差达 20%,但三角学已用于估算目标距离。
4.4.2 文艺复兴至 19 世纪:微积分让弹道 "可预测"
伽利略(1564-1642):抛物线弹道模型
伽利略用几何方法证明了忽略空气阻力时弹道是抛物线,推导出射程公式,这是火力诸元数学化的起点。他在《两种新科学》中写道:"炮弹的路径是一条抛物线,其射程由初速度和仰角决定"—— 这一发现使射程误差从 20% 降至 10%。
牛顿(1643-1727):考虑空气阻力的弹道方程
牛顿在《自然哲学的数学原理》中提出阻力与速度平方成正比的模型,建立了首个完整的弹道微分方程。虽然无法解析求解,但为数值方法奠定了基础。18 世纪的法国数学家欧拉(1707-1783)发明了 "欧拉法",首次实现弹道方程的数值解,使火炮弹道表的编制成为可能。
19 世纪:弹道表与数值分析的胜利
1815 年,英国数学家巴贝奇(1791-1871)设计了 "差分机",用于自动计算弹道表 —— 这是世界上首个机械计算机,本质是用差分法求解弹道方程。到 1900 年,欧洲列强的火炮已能通过查表实现 10km 射程误差 < 5%,比 18 世纪提高了一倍精度。
4.4.3 20 世纪:数值分析与计算机让诸元解算 "实时化"
一战至二战:弹道表与机械计算器
一战时期,火炮射程达 20km,手工计算已无法满足需求。各国采用 "弹道表 + 机械计算器" 的模式:
- 弹道表:预先计算数千种工况的诸元,装订时插值查找
- 机械计算器:如德国的 "莱卡计算器",用齿轮传动实现加减乘除和三角函数计算
这一时期的数学进步是 "有限差分法" 的成熟,使弹道表的精度达 0.5%。
冷战时期:电子计算机与龙格 - 库塔法
1950 年代,电子计算机(如美国 ENIAC)开始用于弹道计算,四阶龙格 - 库塔法成为标准算法。1960 年代,美国 M109 自行火炮的火控计算机可在 10 秒内完成诸元解算,射程误差降至 0.1%—— 这意味着 15km 射程的误差仅 15 米。
同时,卡尔曼滤波算法的出现,实现了 "边打边校":用前一发炮弹的弹着点误差,修正下一发的诸元,使精度进一步提高。
21 世纪:人工智能与实时解算
现代火炮(如中国 PLZ-05)的火控系统采用:
- 多核处理器:每秒可解算 1000 次弹道方程
- 机器学习:通过历史数据训练模型,预测复杂环境下的弹道偏差
- 量子计算(试验中):可在 1ms 内完成传统计算机 1 秒的计算量
这些技术使火炮实现 "动对动" 打击(如打击移动坦克),首发命中率达 80% 以上 —— 这背后是数值分析、优化算法与人工智能的深度融合。
4.4.4 21 世纪:无人机 + AI 重构火力诸元解算范式
无人机与人工智能的结合,正在颠覆传统火力诸元解算模式,其核心是从 "预计算" 转向 "实时感知 - 动态解算 - 闭环修正",数学工具也从单一的微分方程扩展到机器学习、优化算法等。
无人机引导下的诸元解算新流程
-
多源数据融合:融合无人机的激光测距、光学图像、气象传感器数据,建立 "目标 - 环境 - 弹道" 的联合模型,数学上用 "卡尔曼滤波" 实现数据融合:
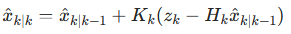

-
快速弹道解算:采用 "神经网络 + 物理模型" 的混合方法:
- 神经网络:用大量弹道数据训练模型,可在 1ms 内输出近似解
- 物理模型:以神经网络结果为初值,用龙格 - 库塔法迭代 2-3 步,得到高精度解(误差 < 0.1%)
这种方法比纯物理模型快 100 倍,满足实时性需求。
-
智能决策系统:基于强化学习,自主选择射击策略(如 "多发同时弹着":不同射角的炮弹同时命中目标),其目标函数为:
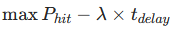

典型案例:美国 "神剑" 制导炮弹的无人机引导系统
"神剑" 炮弹通过无人机激光指示目标,其诸元解算采用:
- 实时气象数据修正:无人机每 30 秒更新一次风速、气温数据
- 弹道预测模型:考虑炮弹自旋导致的马格努斯效应(侧向力)
- 末端修正:在炮弹飞行末段(距目标 3km),用无人机激光测距修正弹道,精度达 10 米以内
实战数据显示,无人机引导使 "神剑" 的命中率从 60% 提升至 92%。
未来趋势:量子计算与量子定位
- 量子计算:可在 1ms 内解算传统计算机需 1 秒的复杂弹道方程,支持 "一炮多目标" 的诸元解算
- 量子定位:无人机搭载量子陀螺仪,定位误差 < 0.1 米,从源头减少坐标转换误差
这些技术将推动火炮精度进入 "米级甚至亚米级" 时代,而这一切的基础,仍是数学工具的持续创新。
结语:无人机让数学 "走出纸面"
无人机的出现,使火力协同中的数学模型从 "理论计算" 变为 "实时应用"—— 密位制的换算不再依赖查表,而是无人机传感器的自动解算;弹道方程的参数不再是经验值,而是无人机实测的环境数据;坐标转换的误差不再累积,而是通过闭环修正不断缩小。
可以说,无人机是数学在火力协同中的 "具象化载体",它让抽象的公式转化为实实在在的打击精度。未来,随着无人机与人工智能、量子计算的结合,数学将在更深层次上重塑火力协同的范式,而 "指哪打哪" 的终极目标,正逐步变为现实。
























 812
812










