第二章优化算法_加权天数-优快云博客

本文链接：https://blog.youkuaiyun.com/blzhizhuang/article/details/118686606

1 Mini-batch梯度下降

1 Mini-batch梯度下降

1 Mini-batch梯度下降的过程

我们将所有的m个样本称为batch，通过向量化方式同时计算m个样本，如果m很大，每次迭代要消耗很长的时间，因为每次都要对所有样本进行运算，我们将这种算法称为Batch Gradient Descent。

为了解决这个问题，可以将batch分成若干个子集，称为mini-batches，然后分别在单一子集上进行样本训练，这种方法被称为Mini-batch Gradient Descent。

假设总的训练样本个数为m=5000000,维度为 $(n_{x},m)$ ，将其分成5000个子集，记每个mini-batch为 $X^{{t}}$ ,维度为 $(n_{x},1000)$ ,相应的输出记为 $Y^{t}$ ,其维度为(1,1000)。

Mini-batches Gradient Descent的实现过程大体如上所示，即先划分T个子集，然后对每个子集进行训练，循环至整个训练集都训练完毕，经过T次循环后所有m个样本集都进行了梯度下降运算，这个过程我们称之为进行了一个epoch,对于batch梯度下降算法而言一个epoch只进行一次梯度下降过程，而对于Mini-batches而言进行T次梯度下降过程。

值得一提的是，对于Mini-batches Gradient Descent可以进行多次epoch训练，并且可以打乱分组重新划分T组子集以获得最优效果。

2 Mini-batches的原理

从上图可以看出Mini-batches在进行迭代时，代价函数曲线会出现振荡现象，但是整体的下降趋势不会发生改变。之所以会存在振荡情况是由于由于划分子集的缘故，导致不同的训练子集出现了个体差异，有部分子集中存在噪声。

上图中蓝色的线是批量梯度下降，紫色的线是随机梯度下降，而绿色的就是这两种算法的折衷，mini-batch gradient descent，它每次迭代过程都能向最优店前进，并且振动幅度较小。

mini-batch gradient descent算法的m一般建议设为2的幂，如果样本总体m较小时建议直接采取批梯度下降。

2 指数加权平均

1 指数加权平均概念

上图是半年内某市的气温变化，将散点图在二维平面上表示出来，似乎温度数据有噪声并且抖动较大，我们需要通过一些处理以便后续操作，这里可以通过移动平均对每天气温进行平滑处理。

设第一天的 $V_{0}=0$ ,这就是第0天的气温值。

第一天的气温与第0天有关： $V_{1}=0.9V_{0}+0.1\theta _{1}$ 其他天数依此类推

有第t天与t-1天的迭代表达式：

由此获得的气温曲线如下所示

这张处理数据的方法被称为指数加权平均，其一般形式如下

$V_{t}=\beta V_{t-1}+(1-\beta )\theta _{t}$

上面的公式里 $\beta$ =0.9，它决定了指数加权平均的天数，这个值表达为 $\frac{1}{1-\beta }$ 。

2 理解指数加权平均

上面是指数加权平均的一般形式，可以发现 $\theta$ 均是原始数据值而 $(1-\beta )$ 类似于指数曲线，从右向左呈指数下降， $V_{t}$ 就是这两个向量的点乘，也就是说指数加权平均就是按照指数趋势对原始数据进行了衰减。

3 指数加权平均的偏差修正

上文中我们得到的指数加权平均结果如上图绿色曲线所示，但实际情况如紫色曲线所示，观察图像会发现在一开始紫色曲线低于绿色，后面趋于重合，之所以出现这种情况是由于我们将 $V_{0}$ 初始化为了0，所以初始值会偏小，解决这个问题要进行偏移校正，即每次计算完 $V_{t}$ 后，都将 $V_{t}$ 除以 $(1-\beta ^{t})$ ，一开始t较小， $(1-\beta ^{t})$ 小于1，会上抬紫色曲线使之与绿色曲线，而到了后面 $(1-\beta ^{t})$ 的值已经接近于1，此时依旧重合，也就达到了我们的目的。

3 优化梯度下降算法

1 动量梯度下降算法

动量梯度下降算法收敛速度快于传统梯度下降算法，做法是在每次训练时，对梯度做指数加权平均处理，然后用得到的梯度值更新权重W和常数项b，实现过程如下所示：

原始的梯度下降算法如上图蓝色折线所示，在这个过程中，梯度下降的振动比较剧烈，尤其对于wb的数值范围差较大的情况，这种情况是由于每个点的梯度是独立存在的，因此形成了折线的效果，前进较慢，类似于前面的气温例子，因此我们可以使用指数加权平均，使梯度与之前的方向产生关联，从而减少振荡，使前进平滑，更容易达到最小值处。

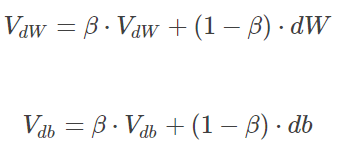
从动量的角度分析，我们可以把 $V^{dW}$ 看作速度V，DW看成加速度a，上述公式实际上就是说当前速度由之前的速度和现在的加速东共同影响，也就是说当前速度是渐变的而非瞬变的，这也就保持了迭代过程的平稳性和准确性，一般设初速度和加速度为0， $\beta$ 初始化为0.9，实际应用的结果比较好。

2 RMSprop

RMSprop是另一种优化梯度下降速度的算法，其参数表达式如下所示：

上图中令水平方向为W的方向，竖直方向为b的方向，从图中可知梯度下降过程在垂直方向上振荡幅度较大，竖直方向较小，因此上述表达式中DW较小，db较大，因此 $S_{b}$ 较大，而 $S_{W}$ 较小，下面的表达式中W方向的下降速度会变快，b方向的会变慢，因此可以防止振荡，在上述表达式中存在分母为零的可能，因此可以在分母上增加一个极小常数 $\varepsilon$ ：