第七章 Logistic回归

最新推荐文章于 2023-12-04 21:02:36 发布
原创 最新推荐文章于 2023-12-04 21:02:36 发布 · 603 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文详细介绍了Logistic回归的背景及其在分类问题中的应用。内容包括分类问题的阐述，Logistic回归的假设函数（使用sigmoid函数），决策边界的定义，代价函数的改写以适应非凸问题，以及高级优化算法如共轭梯度法、BFGS和L-BFGS在Logistic回归中的应用。此外，还讨论了一对多方法解决多元分类问题的策略。

1 分类问题

      在前面几章中我们用线性回归解决了一些问题

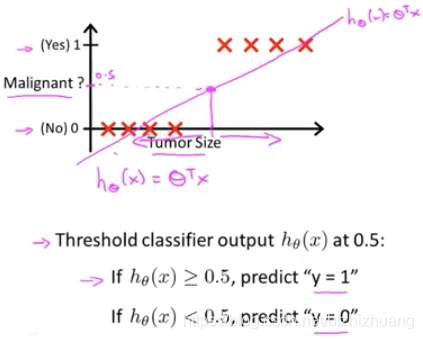
      在上图的分类中我们以0.5作为阈值，大于等于0.5肿瘤为恶性，反之为良性，但是这种情况并不适用于肿瘤大小继续增加的情况：

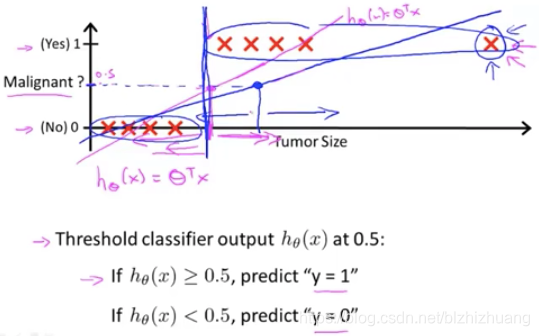
      这里即使样本中标签只有0和1两个值，但是应用线性回归算法后所得的函数结果很有可能远超0和1之间，为此引入了Logistic回归，它应用的范围就是y的取值只在0，1两个离散值之间。

2 假设函数

      由于Logistic回归的取值只在0和1之间，因此假设函数的输出变量同样应该在0和1之间，具体而言：

      h_{\theta }(x)=g(\theta ^{T}x) 

    

最低0.47元/天 解锁文章
多元有序logistic回归_案例分析 | 有序多分类logistic回归及SPSS操作
weixin_42398056的博客
01-11 2万+
一．案例(案例来源：中华护理杂志2018年10期)关于轻度认知障碍(MCI)老年人精神行为症状及影响因素的调查研究。关于轻度认知障碍(MCI)老年人精神行为症状及影响因素的调查研究。方法：采用神经精神问卷(NPI-Q)知情者版，对60名社区初筛为MCI老年人的家属进行调查，根据回收到的有效数据分析MCI老年人精神行为症状的发生情况并研究其影响因素，以期为今后对MCI精神行为症状的预防和干...
用excel做logistic回归分析_用Excel做回归分析的详细步骤
weixin_39557087的博客
12-19 1万+
一、什么是回归分析法“回归分析”是解析“注目变量”和“因于变量”并明确两者关系的统计方法。此时，我们把因子变量称为“说明变量”，把注目变量称为“目标变量址(被说明变量)”。清楚了回归分析的目的后，下面我们以回归分析预测法的步骤来说明什么是回归分析法：回归分析是对具有因果关系的影响因素(自变量)和预测对象(因变量)所进行的数理统计分析处理。只有当变量与因变量确实存在某种关系时，建立的回归方程才有意义...
逻辑回归(Logistic Regression)
西红柿爱喝水的博客
12-23 1354
变量表；逻辑回归模型；代价函数；求解模型参数；一对多。
机器学习——Logistic回归
m0_65098690的博客
12-04 1955
logistic回归的目的是寻找一个非线性函数sigmoid的最佳拟合参数，从而来相对准确的预测分类结果。为了找出最佳的函数拟合参数，最常用的优化算法为梯度上升法，当然我们为了节省计算损耗，通常选择随机梯度上升法来迭代更新拟合参数。并且，随机梯度上升法是一种在线学习算法，它可以在新数据到来时完成参数的更新，而不需要重新读取整个数据集来进行批处理运算。总的来说，logistic回归算法，其具有计算代价不高，易于理解和实现等优点；此外，logistic回归算法容易出现欠拟合，以及分类精度不太高的缺点。
spss进行多元线性回归并分析表格（转载）
热门推荐
woniuhuihui的博客
03-24 2万+
1.如何使用spss进行多元线性回归。 2.分析生成结果，并判断回归是否可行。 一、使用spss进行多元线性回归： 1.输入数据 二、表格结果分析： R方是检验回归是否成功的重要要素之一，DW是残差独立性检验，衡量标准如下： 再看下一个表格： F的值是F检验的结果，他对应的P就是表格中的sig具有重要意义，表格中p=0.015<0.05表明支持原假设，也就是说线性回归方程显著，F检验就是判断回归方程是否显著的。对应的下面的T检验就是判断回归方程的各个变量
回归——逻辑回归
路的博客
07-18 1365
逻辑回归是研究二分类因变量观与一些影响因素之间关系的一种多变量分析方法。但如果因变量是多个类别的，则要用到多分类逻辑回归去研究因变量与一些影响因素之间的关系。输入：因变量 Y 为分类变量，自变量 X 为至少一项定量变量或定类变量。 输出：逻辑回归系数估计以及分类预测的效果评价。根据年龄、月收入、性别、家庭人口等影响因素（自变量）来研究工薪群体的上下班交通工具是公交地铁、自行车、还是私家车（因变量）......
医学统计学第十六章Logistic回归分析.ppt
最新发布
07-29
7. Logistic回归模型的假设检验包括似然比检验等方法，用于检验模型的拟合效果和各个变量的统计显著性。 8. Logistic回归分析的实例中，通过病例-对照研究数据，可以计算得出各个自变量的回归系数估计值，并给出95%...
PyTorch Logistic 回归
02-05
3. Logistic 回归与PyTorch的结合：在PyTorch中实现Logistic回归，需要定义一个单层的神经网络模型，其中包含一个输入层和一个输出层。输出层使用sigmoid函数来确保输出值在(0,1)范围内。 4. 模型构建步骤：首先...
全套清华大学数据分析 统计学 系列课程 06 第六章 Logistic回归 逻辑斯的回归与最大熵模型（共54页）.rar
09-29
**第六章 Logistic回归 逻辑斯的回归与最大熵模型** 在数据分析和统计学领域，Logistic回归是一种广泛应用的预测建模技术，它主要用于处理二分类问题。本章内容源自清华大学的系列课程，全面讲解了Logistic回归的...
logistic回归二分类
10-31
在吴恩达的网易云公开课《深度学习》的第二周课程中，他详细讲解了Logistic回归的原理及其在实际中的应用，特别强调了如何利用Python和NumPy库来实现这一算法。 首先，我们需要理解Logistic回归的核心思想。它不是...
logistic回归因变量的类型_回归分析多分类Logistic回归 ——因变量是多分类变量的回归分析...
weixin_32677301的博客
02-03 1万+
多分类Logistic回归——因变量是多分类变量的回归分析　　【例】研究者将高血压患者按照其生活习惯分类，分成有抽烟习惯的高血压、有饮酒习惯的高血压和没有上述两个习惯的高血压。同时测量其甘油三酯水平和是否有糖尿病，以观察甘油三酯和糖尿病的危害作用。表1　高血压患者分类即相关危险因素资料　　高血压类型的赋值为：高血压+吸烟=1、高血压+饮酒=2、高血压=3；甘油三酯分类并赋值：正常(&lt...
回归分析中变量的赋值
05-15
回归分析中变量的赋值，讲述关于数学建模中变量赋值的问题
机器学习 回归篇（1）——多元线性回归
Cyrus_May的博客
05-08 1506
机器学习 回归篇（1）——多元线性回归摘要线性回归简介python实现运行结果及可视化 摘要 线性回归简介 线性回归问题的重点在于如何求解回归函数的截距和系数。 1、构建代价函数（也叫损失函数）：平均平方误差。 2、通过最小二乘法或其他优化算法进行求解，因为线性回归的代价函数为凸函数，所以一般的经典优化算法用于求解都是适用的，如梯度下降法、单纯形法等等。 python实现 CyrusLinearR...
机器学习（五）logistic回归进行二分类以及多分类（Python代码）
m0_52043037的博客
12-07 7017
   logistic回归虽然名为回归，但实际用于分类问题。   本文将会介绍logistic回归、梯度上升算法以及logistic回归的二分类及多分类问题。  接收输入后能够输出类别。   在二分类中，输出的为0或1。在多分类中，输出的类别就为1，…，n。（多分类可以看作是多个二分类的结合，后文中会介绍）  简要流程如下：       1.回归；       2.求和；       3.Sigmoid。  具体流程为：首先对输入的数据进行回归（即在输入数据的每个特征上都乘一个回归系数），然后将结果相加，将
09- 逻辑回归算法 (LogisticRegression) (算法)
March_A的博客
02-13 603
逻辑回归就是在多元线性回归基础上把结果(result)缩放到 0 ~ 1 之间。hx越接近 1 越是正例，hx越接近 0 越是负例，根据中间 0.5 将数据分为二类。其中hx 就是概率函数~逻辑回归中对应一条非常重要的曲线S型曲线，对应的函数是Sigmoid函数：它有一个非常棒的特性，其导数可以用其自身表示：我们知道分类器的本质就是要找到分界，所以当我们把 0.5 作为分类边界时，我们要找的就是即 ​时，​ 的解~我们知道二分类有个特点就是正例的概率 + 负例的概率 = 1。
一些多元逐步回归的注意事项
SANMUV1ncent的博客
11-27 2348
一些多元逐步回归的注意事项
用excel做logistic回归分析_【数据分析】基础篇，EXCEL回归分析
weixin_36446697的博客
12-04 7623
题记：22:08分，我决定还是写一篇，速度写一篇，赶紧睡觉。最近太忙，痛恨疫情，疫情来了之后真的变成了997工作了。好吧，看看极速下，半小时能不能发一篇原创呢~【什么是回归分析】简单来说：确定变量之间是否存在相关关系。【解决什么问题】简单来说：依据一个或多个变量，预测或控制另外的变量，且估计这种预测的精准度有多高。同时需要注意预测的有效性。【一般怎么做】上学时候一般用SPSS等来做，常见...
用excel做logistic回归分析_利用Excel进行统计分析——入门篇
weixin_35702533的博客
12-28 7625
利用Excel进行统计分析——入门篇。就像大鱼小鱼不能离开水一样，我们这些做科研的医学专业人才，也几乎离不开SPSS了。但SPSS时不时耍个小脾气，突突然就罢工不干了，这可让醉心于科研的我们情何以堪。没电了，还可以用蜡烛或者直流电顶上，但若SPSS罢工了，我们可怎么办?别急， Excel可以帮我们的忙哦。大家可能会说，平常经常用Excel，也没发现统计分析的模块啊。这个嘛，在一些简单设置之后，Ex...
python变量的作用_python变量的作用与定义规则
weixin_39616339的博客
11-23 407
变量的作用：Variables are used to store information to be referenced and manipulated in a computer program. They also provide a way of labeling data with a descriptive name, so our programs can be understoo...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值