第十章 神经网络参数的反向传播算法

目录

1 代价函数

2 反向传播算法

3 理解反向传播

4 梯度检测

5 随机初始化

6 组合到一起

---

1 代价函数

      神经网络一般被定义为两种类型，二元分类和多元分类，假设训练集有m个训练样本，每个包含一组输入输出量x,y。L代表神经网络总层数，在这里设为4层。 表示每层的处理单元个数。

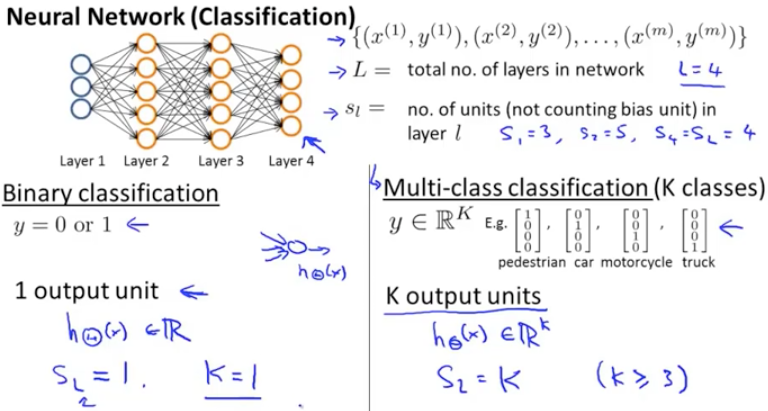
      上图中左边是二分类问题，即输出层有一个输出神经元；右边为多类别分类问题，也就是说会有K个不同的类，输出为K维向量。

      相应于前面的讨论，这里我们要讨论拟合神经网络参数的代价函数，在神经网络中，我们使的代价函数是前面所学Logistic回归中代价函数的一般形式，但是神经网络具有多个输出单元的特性，因此在这里需要做出相应的改变：

      Loistic回归代价函数仅有一个输出单元，即,但神经网络中的 表示第k个输出单元的第i个元素，上式中的求和项为K个输出单元之和。而正则项就是所有参数平方和与 之积。

2 反向传播算法

      正如前几章所学到的，要使代价函数最小化，需要代价函数的值和代价函数关于参数的偏导数，下面从一个训练样本的情况开始：