第二章单变量线性回归_单变量线性回归假设函数-优快云博客

本文链接：https://blog.youkuaiyun.com/blzhizhuang/article/details/118071295

本文讲解了单变量线性回归中的模型表述、假设函数、代价函数以及关键的梯度下降算法。通过实例演示如何利用梯度下降法调整模型参数以最小化平方误差，适合初学者理解线性回归优化过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1 模型表述

从上一章中，我们学习了回归问题，即给出输入，输出连续结果。这一章中我们将就单变量线性回归问题展开讨论，下面首先引入一个根据房屋面积预测房屋价格的例子

我们设定一个数据集作为训练集，由房屋价格和房屋面积组成

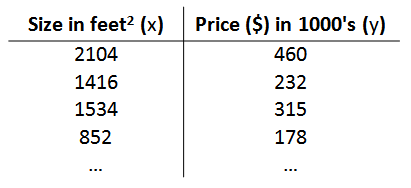
此外，就变量命名做如下约定：

$m$ :训练集样本数量

$x$ : 表示输入变量，也叫输入特征

$y$ :表示输出变量，也叫目标变量

$\left ( x^{i},y^{^{i}} \right )$ ：表示一个训练样本，其中i代表训练样本的行号

通过训练集的学习可以获得一个假设h(hypothesis)，一般表述为一个函数的形式。

2 假设函数

在单变量线性回归中假设函数为： $h_{\theta }(x)=\theta _{0}+\theta _{1}x$ ，其中 $\theta _{0}$ ， $\theta _{1}$ 为模型参数。根据不同的模型参数选取会获得不同的假设函数。

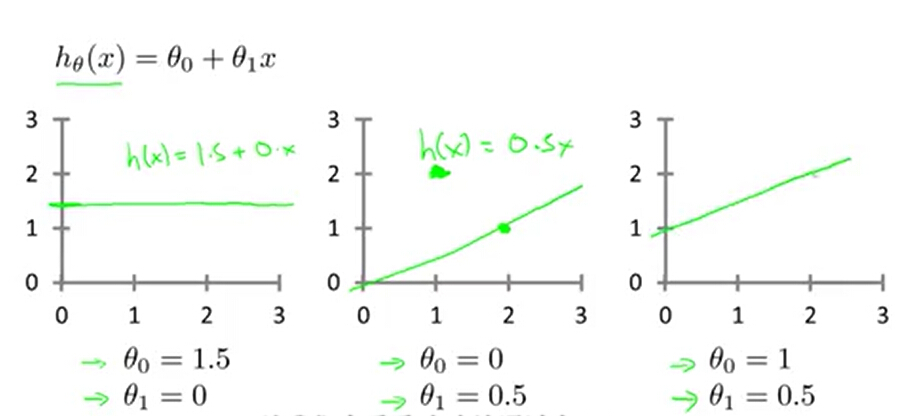
我们需要选取与训练数据拟合程度最高的结果，从代数的角度来看就是要求使假设函数的值最接近y的取值。

3 代价函数

为了使假设函数的值最接近y的取值，我们引入了一个平方误差函数作为代价函数，函数定义为为每个样本的假设函数与y值之差的平方求和，再乘上一个1/2m的系数。

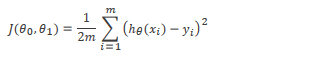
引入代价函数后问题就转化为了求 $J(\theta _{0}^{},\theta _{1} )$ 最小值的问题，为此我们使用梯度下降算法，这个算法可以自动的获取令 $J(\theta _{0}^{},\theta _{1} )$ 最小化的模型系数取值。

4 梯度下降算法

首先确定一个 $\theta _{0}$ $\theta _{1}$ 的初始值，然后通过不断迭代 $\theta _{0}$ $\theta _{1}$ 的值，且每次迭代后J的值降低，最终使J达到最小值，同时确定此时 $\theta _{0}$ $\theta _{1}$ 的值。

梯度下降算法的工作原理

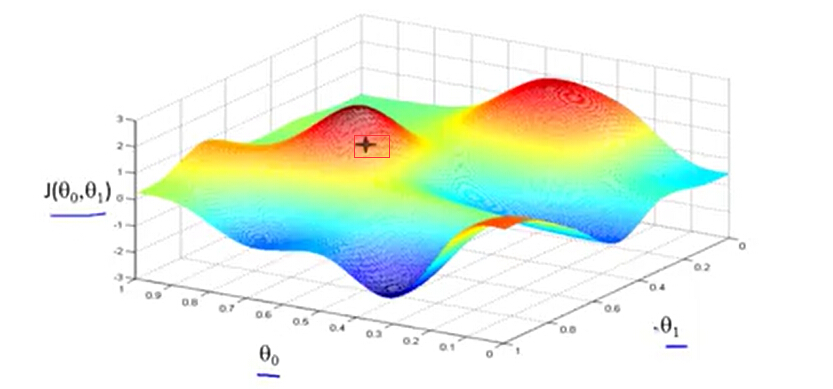
如上图所示，首先对 $\theta _{0}$ $\theta _{1}$ 赋初值（一般可以设为0），即图中标红框点，然后从该点向下移动，而且保证每次移动的方向都是下降最快的方向，最终可以到达图中最凹位置，也就是代价函数最小值的位置。

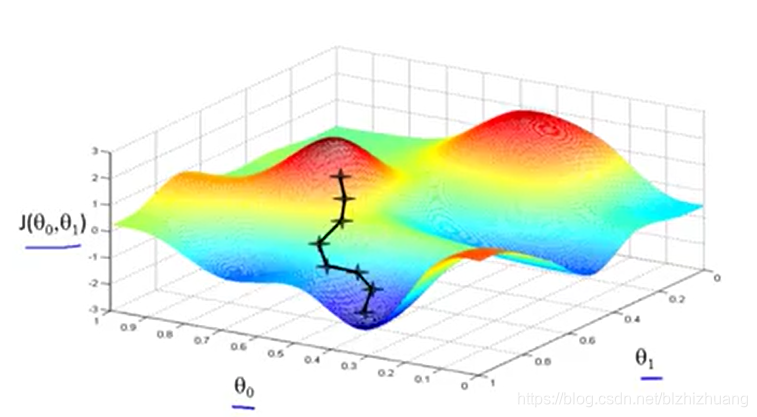
每次移动的方向是下降最快的方向，在数学角度，这个方向被称为梯度的方向，也就是J的导数的方向，对于线性回归而言也就是直线斜率。此外，每次移动的步长同样需要考虑，在这里我们将其定义为学习率 $\alpha$ 。总而言之，在每走一步的过程中 $\theta _{0}$ $\theta _{1}$ 的更新都沿着该点梯度的负方向，而学习率控制着每次更新的步长，公式表述如下图所示：

线性回归中梯度下降的实现

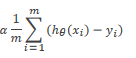单变量线性回归中应用梯度下降算法的过程中，首先对 $J(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}$ 求 $\theta _{0}$ $\theta _{1}$ 的偏导， $\theta _{0}$ 的偏导数为， $\theta _{1}$ 的偏导数为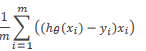。然后带入梯度下降公式中，每一步循环更新。具体公式如下图所示：