求连通块个数（并查集思路）

最新推荐文章于 2025-06-25 20:37:04 发布

夕林山寸

最新推荐文章于 2025-06-25 20:37:04 发布

阅读量3.2k

点赞数 1

CC 4.0 BY-SA版权

分类专栏： # 数据结构----并查集

本文链接：https://blog.youkuaiyun.com/bjfu170203101/article/details/88724145

数据结构----并查集专栏收录该内容

21 篇文章

订阅专栏

本文介绍了在复习DFS时遇到的连通块问题，探讨了如何利用并查集这一数据结构来解决此类问题，特别是针对给定输入n和m，找到最大连通块中节点数量的算法实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

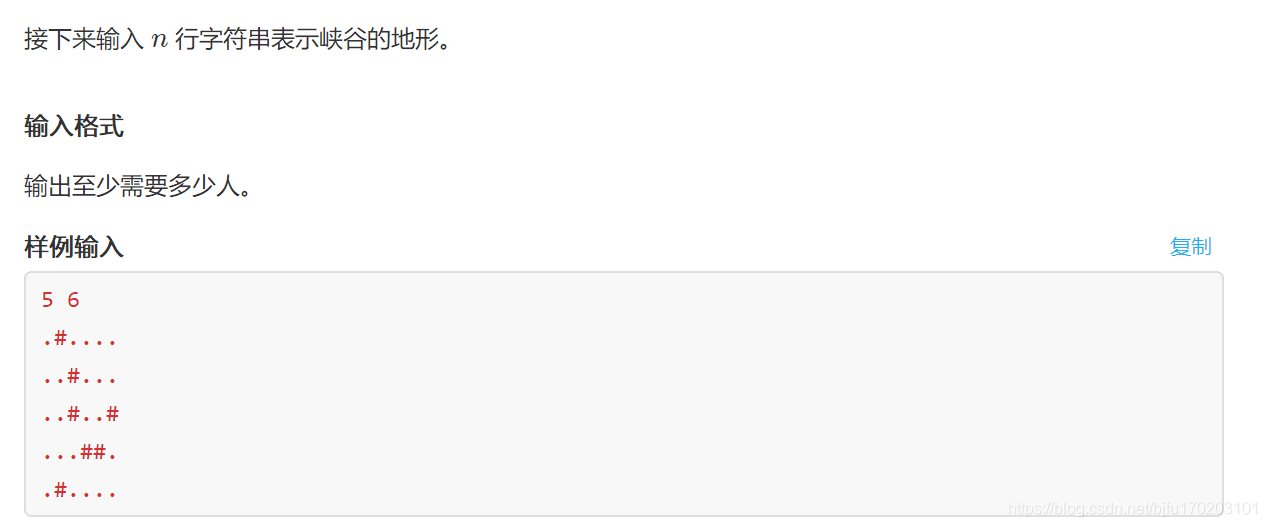
今天复习DFS时做到连通块的题，突然发现并查集也可以搞我就试试没想到还真能弄。。。。

#include <iostream>
#include <string>
using namespace std;
const int M=10000+100;
string s[110];
int fa[M];
int get(int x)
{
    if(fa[x]==x)
        return x;
    return fa[x]=get(fa[x]);
}
void merge(int x,int y)
{
    fa[get(x)]=get(y);
}
int main()
{
    for(int i=0;i<M;i++)
        fa[i]=i;
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++)
        cin>>s[i];
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            if(s[i][j]=='#')
            {
                if(s[i+1][j]=='#')
                    merge(i*m+j,(i+1)*m+j);
                if(s[i][j+1]=='#')
                    merge(i*m+j,i*m+j+1);
            }
        }
    int cnt=0;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            int num=i*m+j;
            if(fa[num]==num&&s[i][j]=='#')
                cnt++;
        }
    cout<<cnt<<endl;
    return 0;
}
/*
5 6
....S*
.**...
.*..*.
*..**.
.T....
*/

下面这道输入n，m 1-1000；求最大连通块中节点个数。并查集实现

#include <iostream>
#include <string>
using namespace std;
const int M=1000000+100;
string s[1100];
int fa[M],sum[M];
int get(int x)
{
    if(fa[x]==x)
        return x;
    return fa[x]=get(fa[x]);
}
void merge(int x,int y)
{
    int gx=get(x),gy=get(y);
    if(gx!=gy)
    {
        fa[gx]=gy;
        sum[gy]+=sum[gx];
    }
}
int main()
{
    for(int i=0;i<M;i++)
        fa[i]=i,sum[i]=1;
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++)
        cin>>s[i];
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            if(s[i][j]=='#')
            {
                if(s[i+1][j]=='#')
                    merge(i*m+j,(i+1)*m+j);
                if(s[i][j+1]=='#')
                    merge(i*m+j,i*m+j+1);
            }
        }
    int ma=0;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            int num=i*m+j;
            if(fa[num]==num&&s[i][j]=='#')
                {
                    ma=max(sum[num],ma);
                    //int q=get(num);
                }
        }
    cout<<ma<<endl;
    return 0;
}
/*
5 6
....S*
.**...
.*..*.
*..**.
.T....
*/