神经网络设计过程

1.神经网络理解

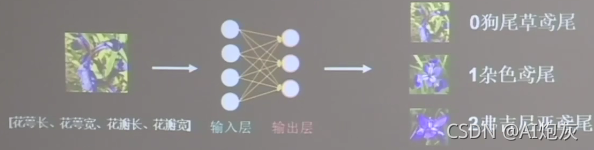
神经网络：采集大量（花萼长、花萼宽、花瓣长、花瓣宽，对应的类别）数据对构成数据集吧数据喂入搭建好的神经网络结构，网络优化参数得到模型，模型读入新输入特征，输出识别结果。

      

      

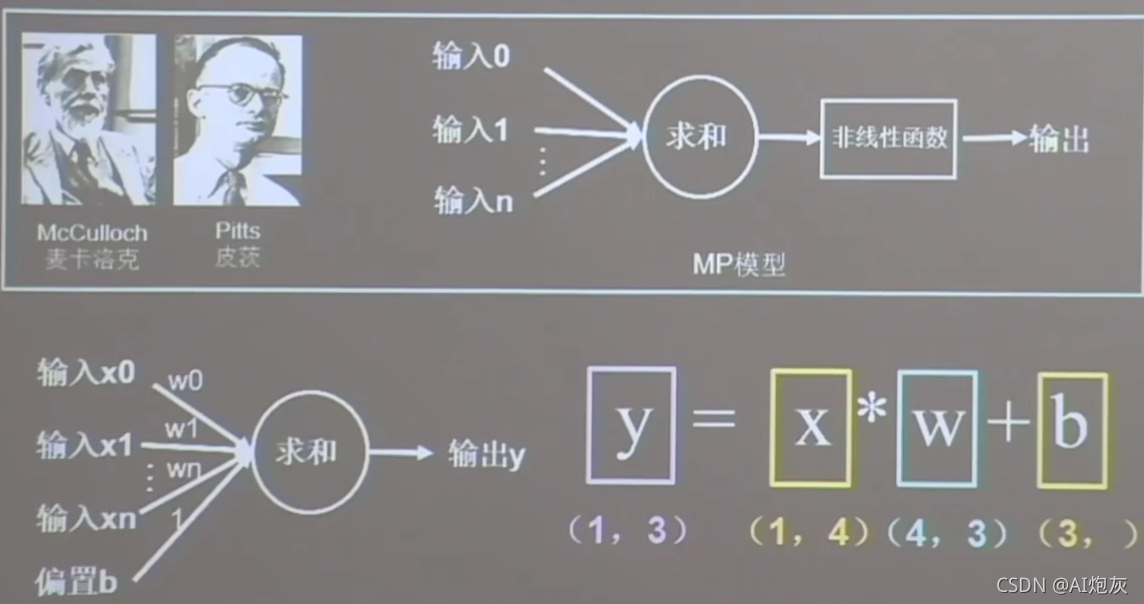
        MP模型是由每一个输入特征和线上的权重求和，在通过一个非线性函数输出。

 2.损失函数

损失函数是指：预测值（y）与标准值（y_）的差距。损失函数可以定量判断W,b的优劣，当损失函数输出最小时，参数W,b会出现最优值。

目的：想找到一组参w,b使得损失函数最小。

梯度：函数对各参数求导后的向量，函数梯度下降方向是函数减小方向

梯度下降法：沿着损失函数梯度下降的方向寻找损失函数的最小值，得到最优参数的方法。

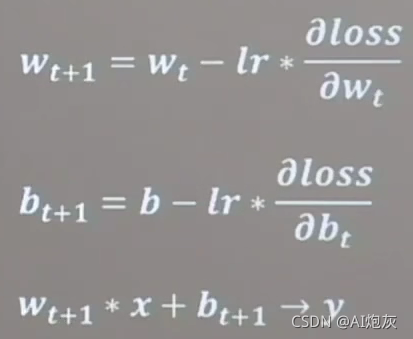
 3.学习率

当学习率设置的过小时，收敛过程将变得十分缓慢，而当学习率设置的过大时，梯度可能会在最小值附近来回震荡，设置可能无法收敛

4.反向传播

从后向前，逐层求损失函数对每层神经元参数的偏导数，迭代更新所有参数。

 5.实例分析

          loss = (w+1)^2,利用梯度下降求解最优的w

import tensorflow as tf

# 设定w的随机初始值为5，并利用Variable设定为可训练
w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40

for epoch in range(epoch):  # 定义顶层循环，表示对数据集循环epoch次
    with tf.GradientTape() as tape:  # with 结构到grads框起了梯度的计算过程
        loss = tf.square(w + 1)
    grads = tape.gradient(loss, w)

    w.assign_sub(lr * grads)  # assign_sub对变量做自减，即：w -= lr*grads 即 w = w - lr
    print("After %s epoch, w is %f, loss is %f" % (epoch, w.numpy(), loss))

                             

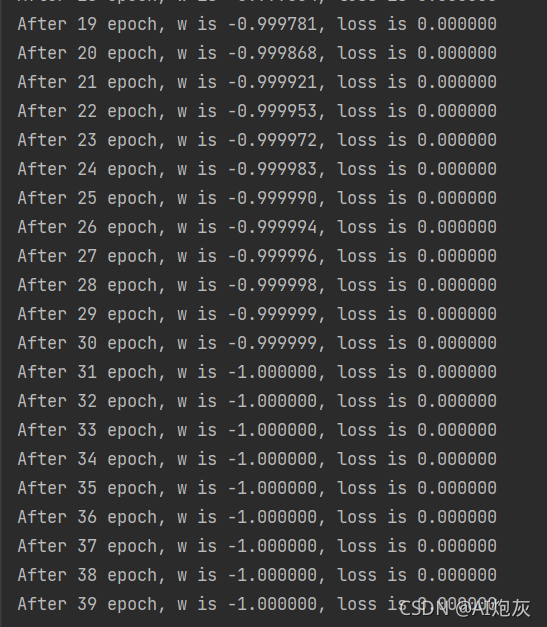
 可以看到在迭代31次开始收敛