资源限制
时间限制:1.0s 内存限制:512.0MB
问题描述
有一长度为N(1<=N<=10)的地板,给定两种不同瓷砖:一种长度为1,另一种长度为2,数目不限。要将这个长度为N的地板铺满,一共有多少种不同的铺法?
例如,长度为4的地面一共有如下5种铺法:
4=1+1+1+1
4=2+1+1
4=1+2+1
4=1+1+2
4=2+2
编程用递归的方法求解上述问题。
输入格式
只有一个数N,代表地板的长度
输出格式
输出一个数,代表所有不同的瓷砖铺放方法的总数
样例输入
4
样例输出
5
分析:
解决问题的关键是找到递归的公式,我们可以把2的数目看成递归的突破点,4里面最多的2的数目就是2个。
种类的通式如下:(假如是4)

值得注意的是,C(n,k)的计算方法:
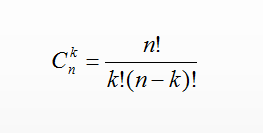
AC代码:
while True




 该博客介绍了如何使用递归算法解决蓝桥杯竞赛中的一个问题,即如何用长度为1和2的瓷砖铺满长度为N的地板。博客给出了问题描述、输入输出格式,并提供了一个样例输入和输出。博主分析了递归公式,指出关键在于确定2的数量作为递归的转折点,并给出了AC代码作为解决方案。
该博客介绍了如何使用递归算法解决蓝桥杯竞赛中的一个问题,即如何用长度为1和2的瓷砖铺满长度为N的地板。博客给出了问题描述、输入输出格式,并提供了一个样例输入和输出。博主分析了递归公式,指出关键在于确定2的数量作为递归的转折点,并给出了AC代码作为解决方案。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















&spm=1001.2101.3001.5002&articleId=104516966&d=1&t=3&u=e6657437fd604371933c2775a3249631)
 1360
1360

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








