蓝桥杯 算法训练 摆动序列Python实现（动态规划）详解

资源限制
时间限制：1.0s 内存限制：512.0MB
问题描述
　　如果一个序列满足下面的性质，我们就将它称为摆动序列：
　　1. 序列中的所有数都是不大于k的正整数；
　　2. 序列中至少有两个数。
　　3. 序列中的数两两不相等；
　　4. 如果第i – 1个数比第i – 2个数大，则第i个数比第i – 2个数小；如果第i – 1个数比第i – 2个数小，则第i个数比第i – 2个数大。
　　比如，当k = 3时，有下面几个这样的序列：
　　1 2
　　1 3
　　2 1
　　2 1 3
　　2 3
　　2 3 1
　　3 1
　　3 2
　　一共有8种，给定k，请求出满足上面要求的序列的个数。
输入格式
　　输入包含了一个整数k。（k<=20）
输出格式
　　输出一个整数，表示满足要求的序列个数。
样例输入
3
样例输出
8

分析：
这是一道很经典的动态规划题，我们这样想，3个数可以组成的序列有2位数，3位数，我们最后的整个序列个数必然是两位数个数加上三位数个数。所以我们用位数作为状态，来动态规划。
初步画一下我们的dp，以k=4为例：

在找到状态方程之前，先填充第二列，第二列是两位数，不难知道不超过n的数组成的两位数有nx(n-1)个，也就是dp[n][1]xdp[n-1][1]:

根据题目给的例子，我们书写出接下来的3位的值：
dp[3][3]应该是含有213,231两个
dp[4][3]应该是213,231,241,243,324,314,341,342，八种。

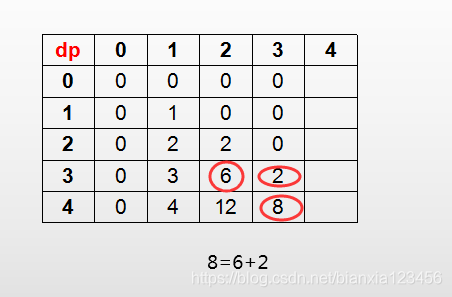
我们可以得出：dp[x][y] = dp[x-1][y-1] + dp[x-1][y]
实现就很简单了

AC代码：