问题描述
如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字,那么我们就说这个数是K好数。求L位K进制数中K好数的数目。例如K = 4,L = 2的时候,所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大,请你输出它对1000000007取模后的值。
输入格式
输入包含两个正整数,K和L。
输出格式
输出一个整数,表示答案对1000000007取模后的值。
样例输入
4 2
样例输出
7
数据规模与约定
对于30%的数据,KL <= 106;
对于50%的数据,K <= 16, L <= 10;
对于100%的数据,1 <= K,L <= 100。
分析:
一开始给题目没读懂,上来就是各种转换进制,我想这题目怎么这么麻烦,后来细读,看题目中放大标红的字体就是,每个数都默认是K进制了(怪自己,惯性思维以为数字都是十进制),然后可以看出,这个题目要用动态规划,拿题目给的例子来说,4进制的2位数,我们可以穷举:
00 01 02 03
10 11 12 13
20 21 22 23
30 31 32 33
符合K好数条件的用红色标出:

而当我们求4进制3位数的时候就会发现:

当百位是0的时候(假设百位是0也能叫一个三位数):
0和1是相邻的,所以直接划掉第二行,其余的就是依赖于两位数时候给出的结果,我们可以直接拿来用,
再写一个百位是1的例子:

百位是1的时候,1与0,1与2相邻,划掉两行,余下的照搬两位数的结果。
所以动态规划的思路和通式都很容易写出来了,我们用列表嵌套列表来实现,K进制作为行,L位数作为列,我们按照列来遍历我们的列表嵌套列表(和二维数组一样)dp:
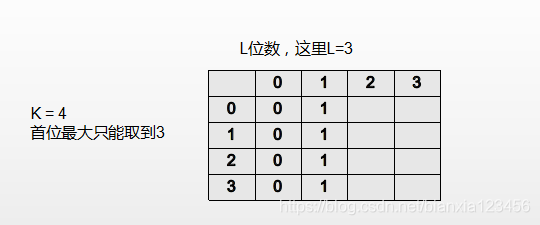
第0列肯定全为0,第一列是一位数,先全部定为1:
按照刚刚手算(小白的卑微,,,)的结果,把上表写满:





 该博客介绍了如何使用动态规划解决K好数问题,即寻找满足特定条件的K进制数。通过分析样例和建立动态规划模型,博主展示了如何填充状态转移矩阵,并给出了递推公式,最后分享了实现代码。
该博客介绍了如何使用动态规划解决K好数问题,即寻找满足特定条件的K进制数。通过分析样例和建立动态规划模型,博主展示了如何填充状态转移矩阵,并给出了递推公式,最后分享了实现代码。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 599
599

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








