这里学习在线性代数中很重要的单位矩阵和逆矩阵。
一、单位矩阵
1、单位矩阵
单位矩阵是一个形状为 (n×n) 的除了对角线为1,其余均为0的矩阵。
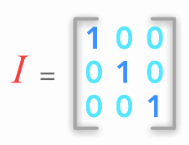
可以使用 Numpy函数eye()创建单位矩阵:
np.eye(3)打印输出如下
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]2、运算示例
单位矩阵乘以向量,结果为原向量。
 本文介绍了线性代数中的关键概念——单位矩阵和逆矩阵。单位矩阵是所有对角元素为1,其余为0的矩阵,乘以向量时保持向量不变。逆矩阵是使得乘积等于单位矩阵的矩阵,用于求解线性方程组。文中通过Python代码展示了单位矩阵的创建、逆矩阵的求解及线性方程组的求解过程。
本文介绍了线性代数中的关键概念——单位矩阵和逆矩阵。单位矩阵是所有对角元素为1,其余为0的矩阵,乘以向量时保持向量不变。逆矩阵是使得乘积等于单位矩阵的矩阵,用于求解线性方程组。文中通过Python代码展示了单位矩阵的创建、逆矩阵的求解及线性方程组的求解过程。
这里学习在线性代数中很重要的单位矩阵和逆矩阵。
单位矩阵是一个形状为 (n×n) 的除了对角线为1,其余均为0的矩阵。

可以使用 Numpy函数eye()创建单位矩阵:
np.eye(3)打印输出如下
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]单位矩阵乘以向量,结果为原向量。
 3274
3274

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


