从坐标轴，距离，相反数去理解原码、反码、补码、移位

原码、反码和补码和unicode一样是编码规则，编码符号整数。与Unicode编码不同，原码、反码和补码不仅用于数据的表示，还直接用于计算机中的算术运算。

从坐标轴，距离，相反数去理解原码反码补码

用数轴理解“减去一个数可以变为加这个数的相反数”：加一个正数往坐标轴右边移动若干单位，加一个负数则向坐标轴左边移动若干单位。

无符号的二进制数在坐标轴中是这样的：

而在限定 4 位时变成了这样:

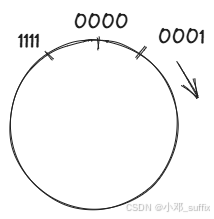
接下来的原码，补码，反码都是要用0-15的二进制去表示正负数，也就是编码。

原码

编码

现在想要在这16个数中区分出正负，最简单的方法是单独拿出一位来表示正负。加入符号位的定义，最高位用来表示正负。

重新编码后，在坐标轴中变成这样：

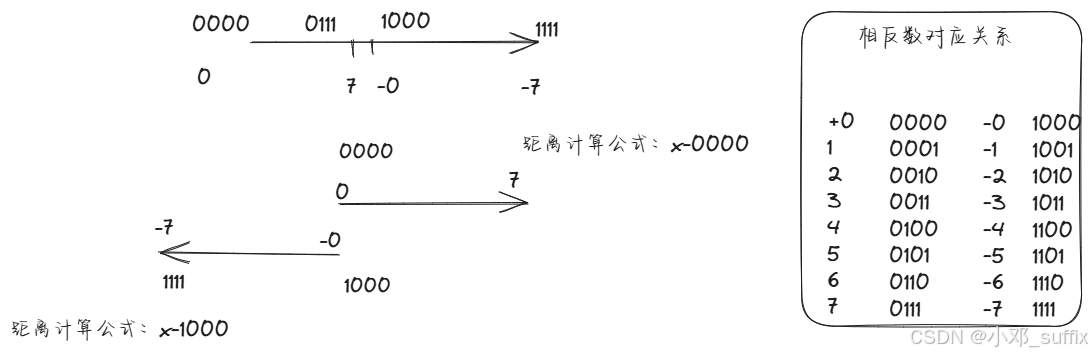
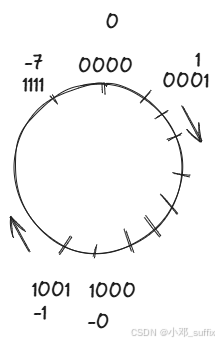
在这样编码的数轴下，零点不统一的正负数并不在用一个数轴中。正数和负数相加不具备任何实际的物理意义。（正+正表示离0000的顺时针距离，负加负的绝对值表示离1000的顺时针距离。），相反数就失去了意义

解码

符号位确定正负，其余确定绝对值

补码

编码

为了避免刻板映像 “补码 = 反码+1”先说补码。

补码：负数x，补码用2n+x的二进制表示。x≡2n+x(mod2n)

在坐标轴中体现如下

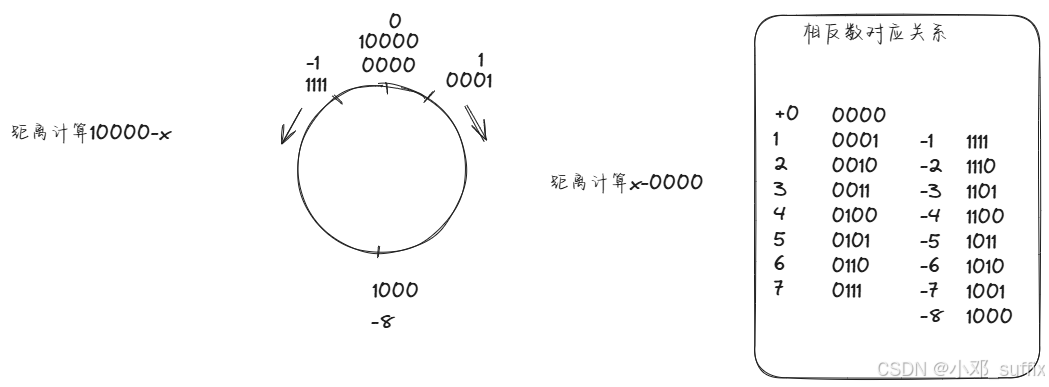
这里 1000 编码为-8 而不是 8，结合原码中符号位的定义，使得最高位仍然具有直接表示符号的作用。在判断是否溢出很有用

零点统一， 距离零点距离表示绝对值大小。正负绝对值增长方向相反，加减可以表示为在坐标轴上顺逆时针移动。

如-8(1000)+1(0001)相当于-8 顺时针走一步（1001）=-7

如 5(0101）+(-1)（1111）,5 逆时针走1步到 0100 = 4

减去一个数可以转变为加这个数的相反数。

可以看到整个补码的定义，完全没有涉及到反码，

强调补码 = 反码+1 是由二者定义下产生的一种必然的运算规则，而不是补码的定义，补码的定义是基于模运算的，而不是基于反码

就算没有反码，极端一点计算机硬件计算完成以后就查表来确定补码表示的是那个数（解码）也是完全可行的

解码

编码后如何知道1111表示的是-1呢，不可能真的查表吧

1.符号位确定正负，对模2^n ,求同余数。（负数就是减去2^n）

2  符号位确定正负，确定是负数后按位取反+1得到绝对值

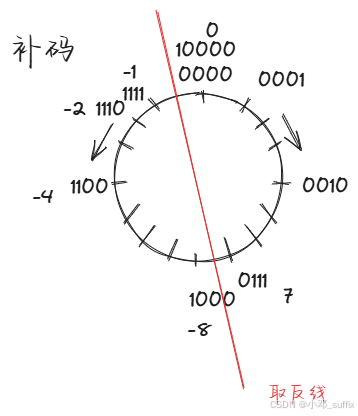
反码

编码

反码的编码方式是用 0001 的按位取反(1110)表示-1

在坐标轴中

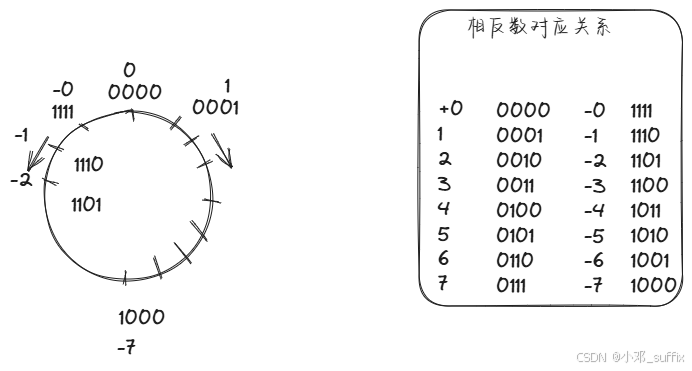
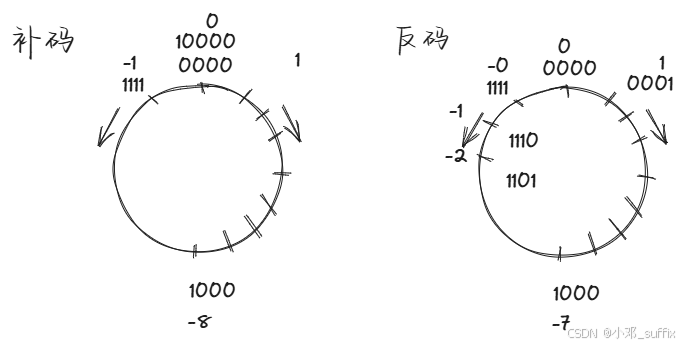
对比补码和反码的两个图就能很直观的看出为什么负数的补码 = 反码+1；

例 -1 的补码 1111 反码 1110

也可以这样理解：为了解决反码零点坐标不统一的问题，将负数反码编码顺时针挪动一位，就得到了补码。此时相反数相加仍然为0，且0点统一

解码

1 符号位确定正反，负数按位取反得到绝对值

关于移位

Java 只有 3 个移位运算符：左移（<<）、带符号右移（>>）和无符号右移（>>>)

左移: 末尾补0，相当于乘2

右移: 高位补符号位 相当于除2

可以结合数轴看一下补码部分

关于左移溢出：数值位第一位与符号位不同时，再乘2 必定溢出，所以如果左移发生符号位改变就表示溢出了。

以四位为例子

正数： 0100 表示4，4*2=8 而四位二进制表示正数范围为0-7

负数 10 11 表示-5 ， -5*2=-10，四位2进制表示负数范围为-1到-8

关于负数右移

右移最后一位是0是1 不影响结果，

表现在正数上：6和7,4和5 右移结果一样。结尾是1比结尾是0 的数 数值部分大一，也就是说2n和2n+1右移结果一样，即除2 抛弃余数（向下取整）

表现在负数上：-8和-7，-6和-5 右移结果一样。对负数结尾是1 比结尾是0 的数 数值部分小1 。-（2n） 和-（2n-1）右移结果一样，即除2有余数的话数值部分要加1（向下取整），

而C++11 和java的除法操作本身都是向零取整的，有小数部分直接除去，所以对于负数来说右移操作和除2操作不完全相等。

顺便提一句取余‘%’，规定商的结果向0取整，而为了(m/n)*n+m%n=m，(m/n)*n的绝对值是小于m的绝对值的 ，所以余数的符号一定是与被除数m相同的

> -7(1001)>>1   =(-4)1100

>  -7/2=-3

总结

表现在数值上 正数右移相当于除2 抛弃余数（向下取整），而负数右移有余数，数值部分要加1 （也是向下取整）。

所以右移操作是除2 向下取整，而语言本身'/'是向零取整，对正数来说二者表现一样，对负数来说‘>>’结果比'/2'结果小1.