[USACO08NOV]玩具Toys

最新推荐文章于 2025-01-24 20:38:09 发布

白酒蒿

最新推荐文章于 2025-01-24 20:38:09 发布

阅读量276

点赞数 3

分类专栏：三分

本文链接：https://blog.youkuaiyun.com/baijiuhao/article/details/99623171

版权

三分专栏收录该内容

1 篇文章

订阅专栏

算法：三分+贪心

1.读题之后的第一件事是明确目标和问题：

第一步有同学可能会往DP的方向思考（比如蒟蒻我）。因为我们要处理的问题是我需要买多少个玩具，并且每天分别分多少个给n1，多少个给n2才能使得总和最小。
但是，在DP之前一定要仔细想一想，有一个算法也可以处理部分DP问题但是比DP更优秀，那就是贪心。

但是我们要证明贪心是正确的。我们不妨假设c1与c2是商店里玩具的另一种价格且数量有限，sum为1~D天派对所需要的玩具总量，无论如何我们都要从c1,c2,tc这三种价格购买sum个玩具，显然买价格越便宜的越好。

2. 第二步将问题拆分，往简单的方向去思考

关于拆分的方向，这里是根据算法以及自身经验来的（如果是大佬的话完全可能能够一次性到位吧）因为我们要让总的金额最少，并且要让每天派对拥有足够的玩具，我们必须要选择最便宜的方案。

为了说明方便，我们这里的所有玩具消毒只按天数付钱。也就是我可以先把所有玩具免费消毒，然后根据取回当天距离消毒当天的天数，划分n1，n2两个档次。如果n1=1，n2=2，一个玩具在第一天送去消毒，在第二天取出来的价格就是c1，但是如果在第三天取出来价格就是c2了（相当于玩具不用立刻在n1天或者n2天取出，可以存放很长一段时间）

设 $c 1 > c 2$ （接下来的分析是对于每天单独贪心的情况）

如果 $c 2 > t c$ 也就表明与其送去消毒不如天天买新玩具，这个时候只需要输出 $t c * s u m$ 就可以啦

如果 $c 1 > t c > c 2$ 或者 $t c > c 1 > c 2$ 且c2要快一些那么我们只需要将玩具分给从商店买，和n2天消毒就行

如果 $t c > c 1 > c 2$ 且c2 比较慢，这个时候我们要仔细斟酌一下啦。

到这里与其考虑每天的分配方式，我们不如从总量分析（因为这里每天分析会变的很麻烦）我们不妨假设我们一共要买x个玩具，那么我们设f(x)表示满足每天需求前提所需要的最小费用，其中x表示购买的的新玩具的个数。g(x)表示在1~D天内把认为需要送去消毒的旧玩具送去消毒花费的费用。从商店购买的费用算为 $t c * x$ ,总共的费用就可以算为： $f (x) = g (x) + t c * x$ ，并且这函数的斜率是单调的。

为什么？！

如果新玩具很多，那么g(x)就会特别小。因为新玩具已经满足了派对的需求所以不需要在送一些去洗了。并且存在 $g (x - 1) - g (x) > = g (x) - g (x + 1)$ 可以这样来考虑，因为玩具数少需要快洗，花的钱就比较多。并且abs(k)就要大一些，函数图像也要抖一些。但是如果玩具数量多，就会选择慢洗。所以abs(k)就要小一些，函数图像也就要缓一些。
反向表示带入可得： $f (x) - f (x - 1) < = f (x + 1) - f (x)$ 于是f(x)的斜率也是单调递增的。
那么斜率单调递增的函数会有哪些图像呢：

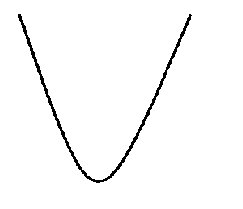
由图可见这种函数是单峰的，所以可以三分。

如果这里理解不了的同学可以这样意会：如果玩具买多了就会浪费一部分钱，因为多买的部分可以用消毒的费用来代替，如果买少了反而要在消毒上面花更多的钱。所以这个函数就是单峰的！

单峰的函数自然而然会联想到三分，所以这道题到这里已经解决了一半了。

3.接下来要完成的任务便是怎么求出这个总花费。

我们依旧在 $t c > c 1 > c 2$ 且c2 比较慢这情况下面思考。

那么只考虑对每天进行贪心，就是每天都洗最便宜的衣服，求出来的答案是否是最优的呢？

很明显不完全正确！ 我这里举个例子：D=4,N1=1,N2=3,C1=3,C2=1,Tc=4,D1=3,D2=1,D3=1,D4=4;当我们按照上述方法贪心的时候求出来的结果是27，但是正解是25，原因就是我们在第三天的时候，贪心会选择来自第一天的玩具（因为这个贪心只考虑当前最便宜的玩具不考虑天数）。

但是如果我们选择跟第一天玩具相同价格的第二天的玩具。虽然对于第三天来说花费是相通的，但是对第四天来说花费就有所不同了（大家可以手工模拟一下这里就不再做详细解释了）。

所以我们从上面的例子得到了一个结论，在价格相同的情况下我们应该选择消毒时间最近的玩具，这样消毒时间远的玩具价格就会降低。

算法到这里大概就解释清楚了 ~~（吧）~~然后是代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=100000+5;
const int inf=1000000000; 
int d,n1,n2,c1,c2,tc,l,r,t[maxn];
struct code
{int Day,toys;};
deque<code> n,o,m;
//我们这里用了三个双端队列，表示n,o,m。
//n表示从开始消毒的那天到今天少于n1天的玩具
//m表示消毒了至少有n1天但是不满足n2天的玩具
//o表示已经消毒了至少n2天的玩具 
void add(int day,int toy)
{
	code now;
	now.Day=day,now.toys=toy;
	n.push_back(now);
}
void newch (int x)
{
	while (n.size()&&x-n.front().Day>=n1)//这里从队首开始讨论，因为队首都是早先被压入的，时间比较久 
	m.push_back(n.front()),n.pop_front();
	while (m.size()&&x-m.front().Day>=n2)
	o.push_back(m.front()),m.pop_front();
}
int Find(int x)
{
	while (n.size()) n.pop_front();//记得清零！ 
	while (o.size()) o.pop_front();
	while (m.size()) m.pop_front();
	int money=(tc-c2)*x;
	//因为在下面的讨论里面我们要把所有的玩具当成消毒过的。
	//但这里是直接购买的玩具，所以要减去c2 
	add(-200000,x); //设成-200000是为了方便讨论（不清楚的可以手工模拟一下） 
	for (int i=1;i<=d;i++)
	{
		int rest=t[i];
		newch(i);//在这里进行新旧交替的操作，相当于题解中我们按照天数堆对消毒进行付款，而不明确的分类 
		while (rest&&o.size())//先选择便宜的 
		{
			if (o.back().toys>rest)//这里从back弹出就是相同价格选择清洗时间比较近的（下同） 
			o.back().toys-=rest,money+=rest*c2,rest=0;
			else 
			rest-=o.back().toys,money+=c2*o.back().toys,o.pop_back();
		}
		while (rest&&m.size())
		{
			
			if (m.back().toys>rest)
			m.back().toys-=rest,money+=rest*c1,rest=0;
			else 
			rest-=m.back().toys,money+=c1*m.back().toys,m.pop_back();
		}
		if (rest) return inf;//inf就表示玩具数量不足以满足派对的需求 
		add(i,t[i]);
	}
	return money;
}
int three()
{
	 r=r+1;
	while (r-l>2)//当l和r足够接近的时候就可以手工跳出了 
	{
		int x=(2*l+r)/3,y=(2*r+l)/3;
		int a=Find(x);
		if (a!=inf&&a<=Find(y)) r=y; 
		else l=x;
	}
	int ans=Find(l);
	for (int i=l+1;i<=r;i++)
		ans=min(ans,Find(i));
	return ans;
}
int main()
{
	scanf("%d%d%d%d%d%d",&d,&n1,&n2,&c1,&c2,&tc);
	if (n1>n2)//保证n1是快洗 
	swap(n1,n2),swap(c1,c2);
	if (c1<c2) c2=c1;//如果快的价格反而要低一些为什么不选择快的呢
	//因为后面的讨论是根据慢的比较低这个条件来的，所以这里需要赋值。 
	for (int i=1;i<=d;i++) scanf("%d",&t[i]),r+=t[i];
	//为什么二分的上限是玩具的总数，因为我最多把所有玩具买下来啊 
	printf("%d",three()); 
}

参考资料：官方标准程序（如下）

#include <stdio.h>
#include <stdlib.h>
#include <algorithm>

using namespace std;

#define MAX (100005)
#define INF (1000000000)

int T[MAX];
int queue[MAX], num[MAX];
int sn,sm,so,en,em,eo;
/* These variables control the queue and point to the start 
 * and end of new, middle, and old toys, respectively. 
 * New toys are ones washed less than N1 days ago, old toys are 
 * washed at least N2 days ago, and middle toys are all the rest.
 * We essentially keep three queues in a single array, but the manner
 * in which we add/remove elements guarantees that we never have to
 * worry about memory overlap.
 */

int D,N1,N2,C1,C2,Tc;

inline void add_new(int x,int q){
  queue[en]=x;
  num[en++]=q;
}

void flush_new(int x){
  while(sn!=en && x-queue[sn] >= N1) { num[em]=num[sn]; queue[em++]
= queue[sn++]; }
}

void flush_mid(int x){
  while(sm!=em && x-queue[sm] >= N2) { num[eo]=num[sm]; queue[eo++]
= queue[sm++]; }
}

int f(int t){ //find the minimum cost given that we use t toys
  sn=sm=so=en=em=eo=0;
  int r = (Tc-C2)*t;
  /*
   * In the following algorithm, we pay even to wash the initial toys, so 
   * we have to subtract this out of our initial cost estimate for 
   * purchasing the toys. This is valid as long as we use all of the toys 
   * we purchase (which is why we start the ternary search at tsum+1 
   * instead of 5000001).
   */
  add_new(-200000,t);
  for(int d=0;d<D;d++){
    flush_new(d); flush_mid(d); //move any toys toys whose status changes 
      //from being new to middle or middle to old to the appropriate queue
    int i = T[d];
    while(i > 0){ //we deal with the toys in batches to make 
      //the runtime of this function O(N) instead of O(sum ti)
      if(so!=eo){ //if there are any old toys
        if(num[eo-1] > i){ //if this batch has more toys than we need, we can stop here
          r += C2*i;
          num[eo-1]-=i;
          break;
        }
        else { //otherwise, use all toys in this batch
          r += C2*num[eo-1];
          i -= num[eo-1];
          eo--;
        }
      }
      else if(sm!=em){ //else if there are any middle toys
        if(num[em-1] > i){
          r += C1*i;
          num[em-1]-=i;
          break;
        }
        else {
          r += C1*num[em-1];
          i -= num[em-1];
          em--;
        }
      }
      else return INF; //if there are no available toys, 
        //we can't find a solution with this many toys
    }
    add_new(d,T[d]); //put the toys we used today back into the queue of toys
  }
  return r;
}

int ternary_search(int s,int e){
  while(1){
    if(e-s <= 2){ //when e-s is small enough that our ternary search 
      //can get stuck, just handle the end manually
      int m = f(s);
      for(int i=s+1;i<e;i++) m = min(m,f(i));
      return m;
    }
    int x = s+(e-s)/3, y = s+2*(e-s)/3; //sample values 1/3 and 2/3 
      //of the way through the remaining interval
    int a = f(x); //f(x) = -1 if x was too few toys to have enough toys each day
    if(a!= INF && a <= f(y)) e=y;
    else s=x;
  }
}

int main(){
 scanf("%d%d%d%d%d%d",&D,&N1,&N2,&C1,&C2,&Tc);
  if(N1 > N2){ //set N2 to be greater than N1
    N1 ^= N2; N2 ^= N1; N1 ^= N2;
    C1 ^= C2; C2 ^= C1; C1 ^= C2;
  }
  if(C1 < C2){ //if faster way is cheaper
    C2 = C1; //then set its cost to that of the slower way, 
      //since we could always just use the slower way instead
  }
  int tsum = 0;
  for(int i=0;i<D;i++) { scanf("%d",&T[i]); tsum += T[i]; }
  printf("%d\n",ternary_search(0,tsum+1));
  return 0;
}

因为本蒟蒻太菜了，所以一来想到的是Dp（可能DP做多了，都忘了老本行贪心了），然后搞了个五维的出来，并且还不能优化（那么问题来了，为什么会有状态压缩的标签呢），总之就是我太菜了第一次没做出来。

于是本蒟蒻就很不要脸的去网上找题解了（emm）,可能是年代太早了，网络上的题解相当的少，而且相当的简洁。可能一般做到这里的人，都已经学会网络流了（餐巾问题呢）所以本蒟蒻看不懂呢qwq。花了一天的时间终于把这道题A掉了，然而为了造福后面解这道题的人，这篇题解就写的特别的啰嗦（害怕有人看不懂emm）

另外是关于函数的部分，其实之前有很多博客都证明了单峰函数，但是函数的含义并没有详细的给出。这里进行了比较详细的说明