数字逻辑基础
常用逻辑门
| 逻辑门类型 | 逻辑表达式 | 真值表(输入 A、B,输出 Y) | 逻辑关系描述 |
|---|---|---|---|
| 非门 | A=0 → Y=1; A=1 → Y=0 | 输入输出相反,单输入单输出 | |
| 与门 | A=0,B=0 → Y=0; A=0,B=1 → Y=0; A=1,B=0 → Y=0; A=1,B=1 → Y=1 | 全 1 出 1,有 0 出 0 | |
| 或门 | A=0,B=0 → Y=0; A=0,B=1 → Y=1; A=1,B=0 → Y=1; A=1,B=1 → Y=1 | 有 1 出 1,全 0 出 0 | |
| 与非门 | A=0,B=0 → Y=1; A=0,B=1 → Y=1; A=1,B=0 → Y=1; A=1,B=1 → Y=0 | 与门输出取反:全 1 出 0,有 0 出 1 | |
| 或非门 | A=0,B=0 → Y=1; A=0,B=1 → Y=0; A=1,B=0 → Y=0; A=1,B=1 → Y=0 | 或门输出取反:全 0 出 1,有 1 出 0 | |
| 异或门 | A=0,B=0 → Y=0; A=0,B=1 → Y=1; A=1,B=0 → Y=1; A=1,B=1 → Y=0 | 输入不同出 1,相同出 0 | |
| 同或门 | 输出与异或门相反 | 输入相同出 1,不同出 0。 |
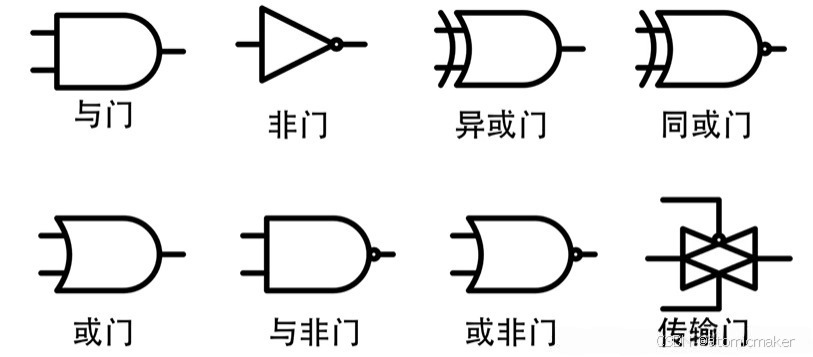
逻辑关系描述
这里的逻辑表达式和离散数学中的是类似的,只是符号稍微有些不同,最大项最小项相关定义可以去看离散数学篇:
逻辑函数的化简
1.代数化简法
利用逻辑代数的基本定理,对逻辑函数进行等值变换,消除多余的乘积项和变量(离散数学中的化简方法)。
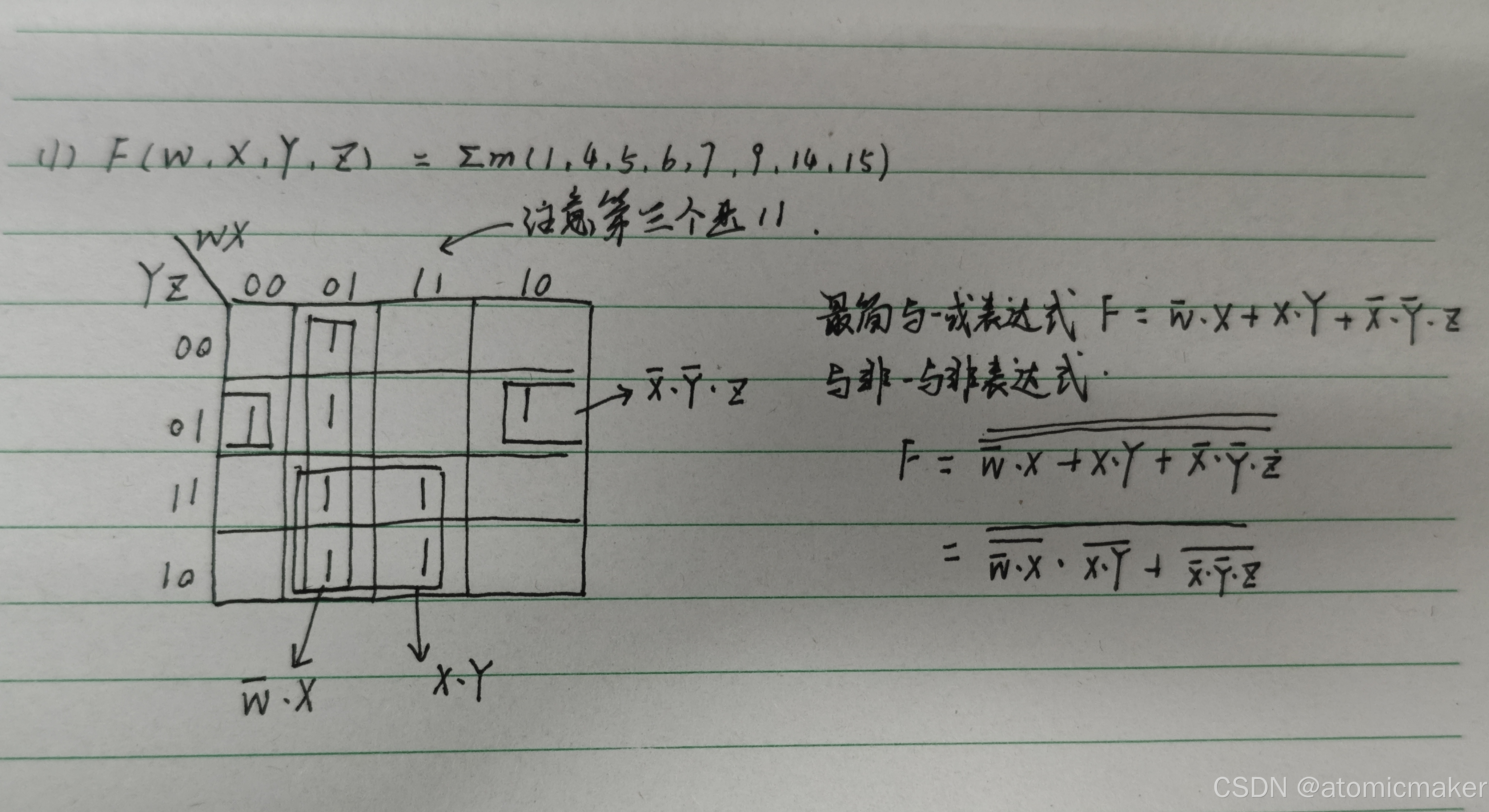
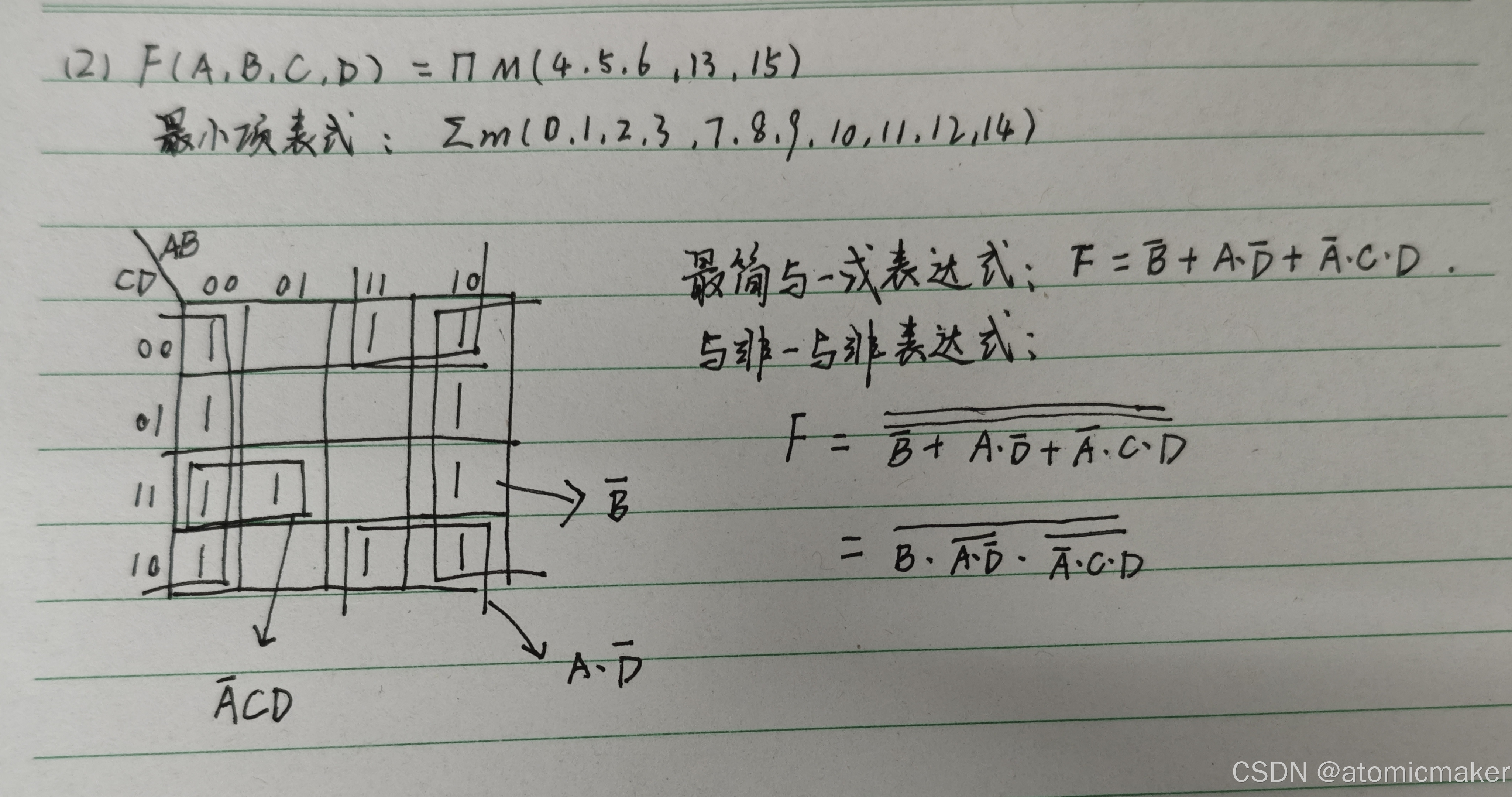
2.卡诺图化简法
卡诺图是 n 变量最小项的方格图,相邻方格(包括上下、左右、四角)对应的最小项只有1 个变量不同,利用相邻项可合并消去不同变量的原理化简,适用于变量数 (n≤4) 的函数。
- 在卡诺图中将真值表中输出值为1时对应的最小项所在的单元格标注为1。
- 每个单元对(最大矩形框,框内方格数为2^n)都可以消除一个不相同的变量而留下相同的变量。
下面用一个例题理解一下:

组合逻辑电路
组合逻辑电路概述
组合逻辑电路是由逻辑门(与、或、非、与非等)组合而成的数字电路,其核心特点是:
- 电路无记忆性:任意时刻的输出仅由当前时刻的输入决定,与电路过去的输入状态无关。
- 结构无反馈:电路中不存在从输出到输入的反馈通路,信号仅从输入单向流向输出。
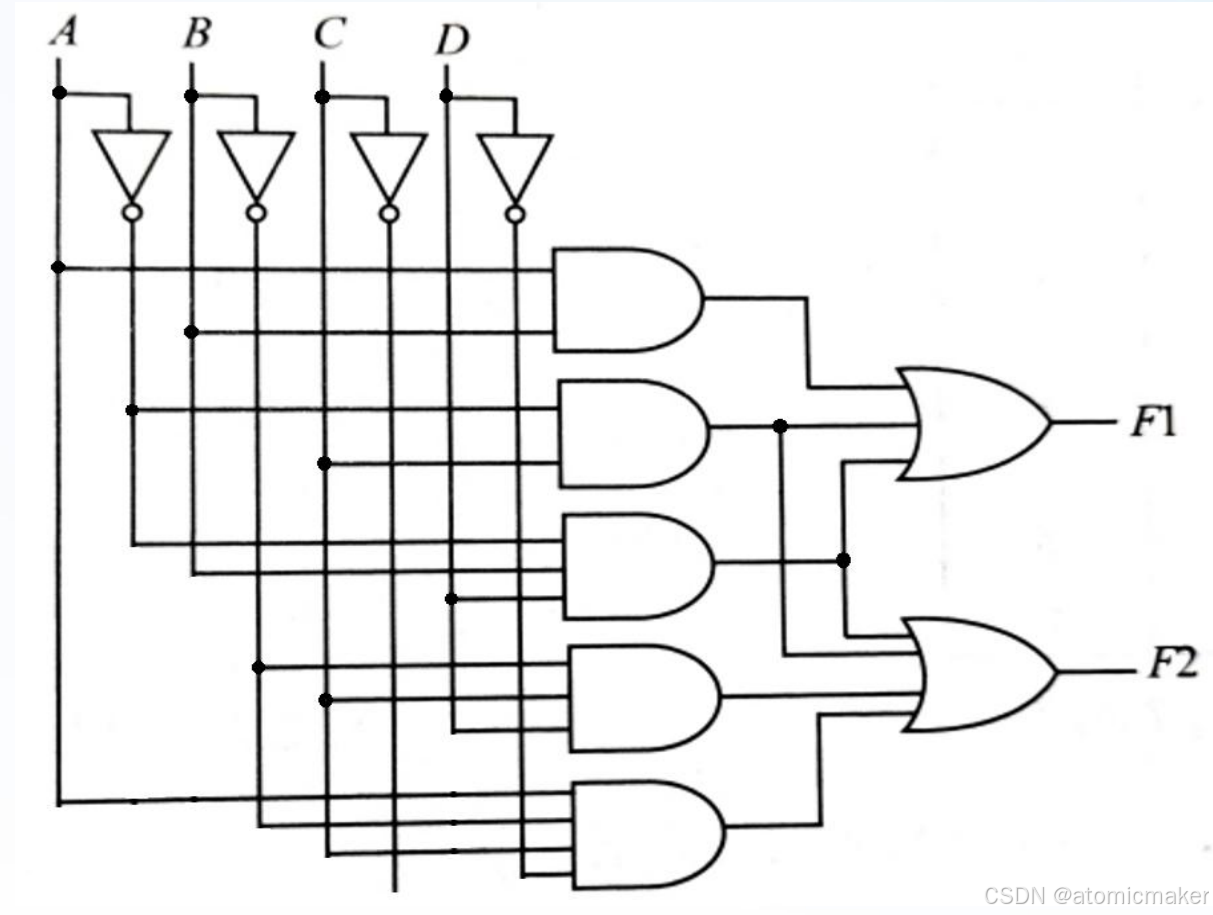
1.组合逻辑电路的分析(已知电路求表达式)
例如,写出下面电路的逻辑表达式
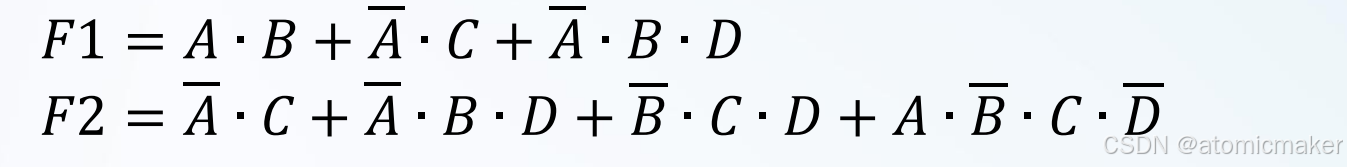
2.组合逻辑电路的设计(已知真值表求电路)
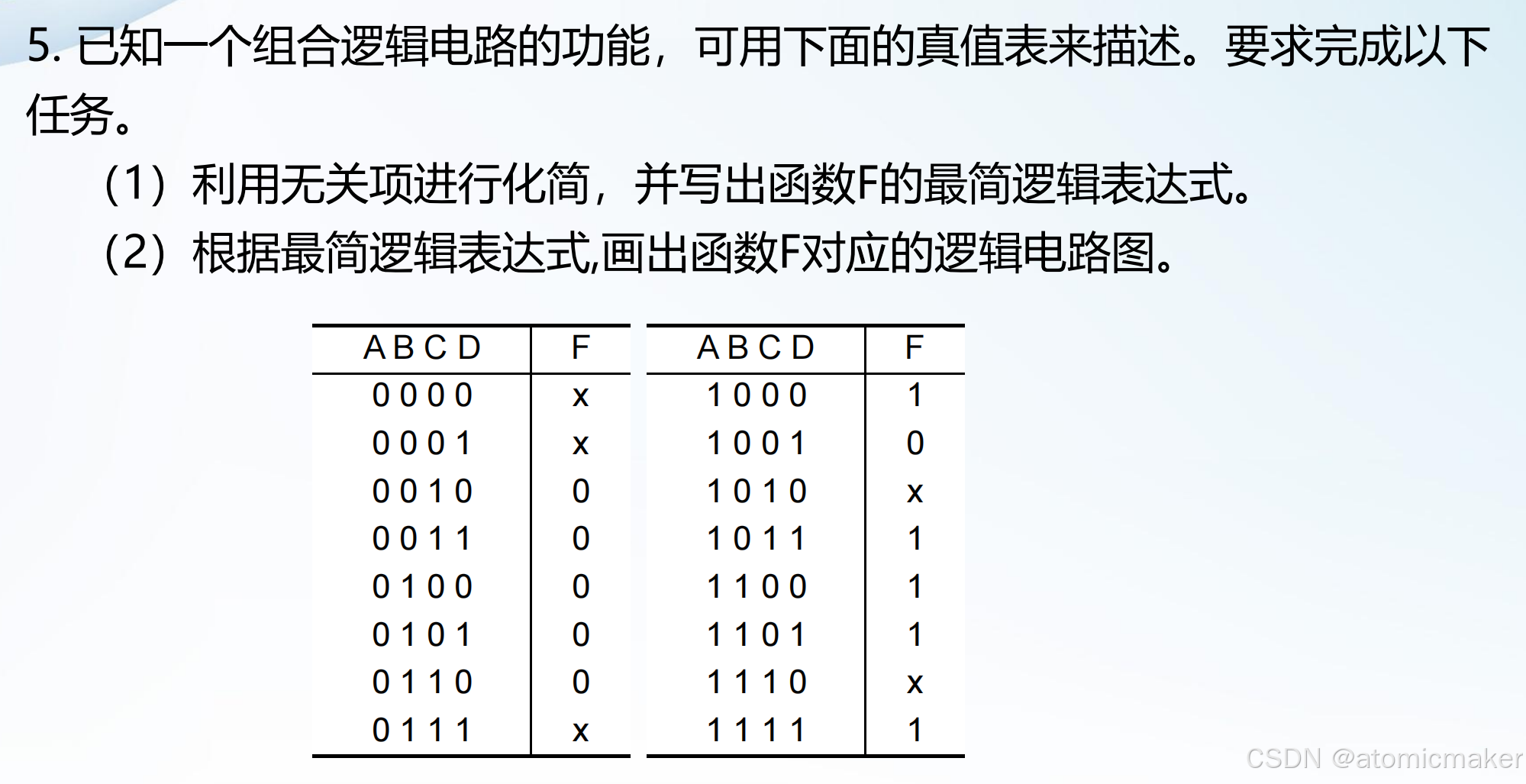
根据真值表画出卡诺图,以此得出最简逻辑表达式,最后画出电路图
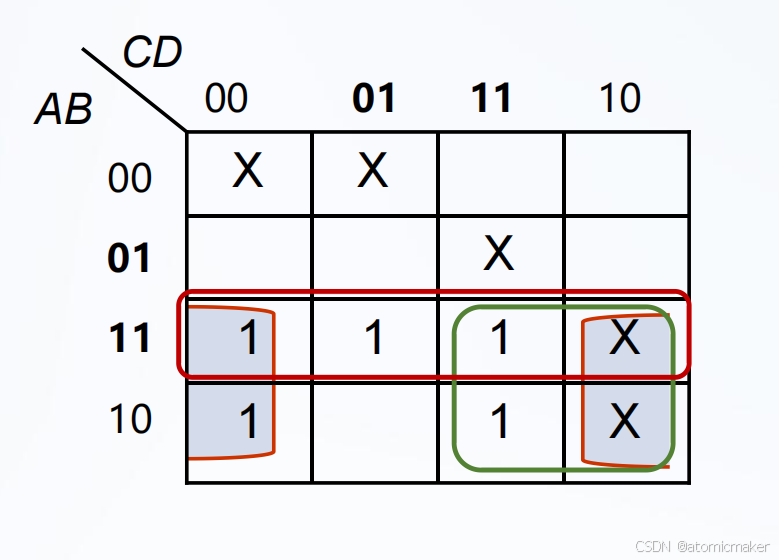
![]()

典型组合逻辑部件设计
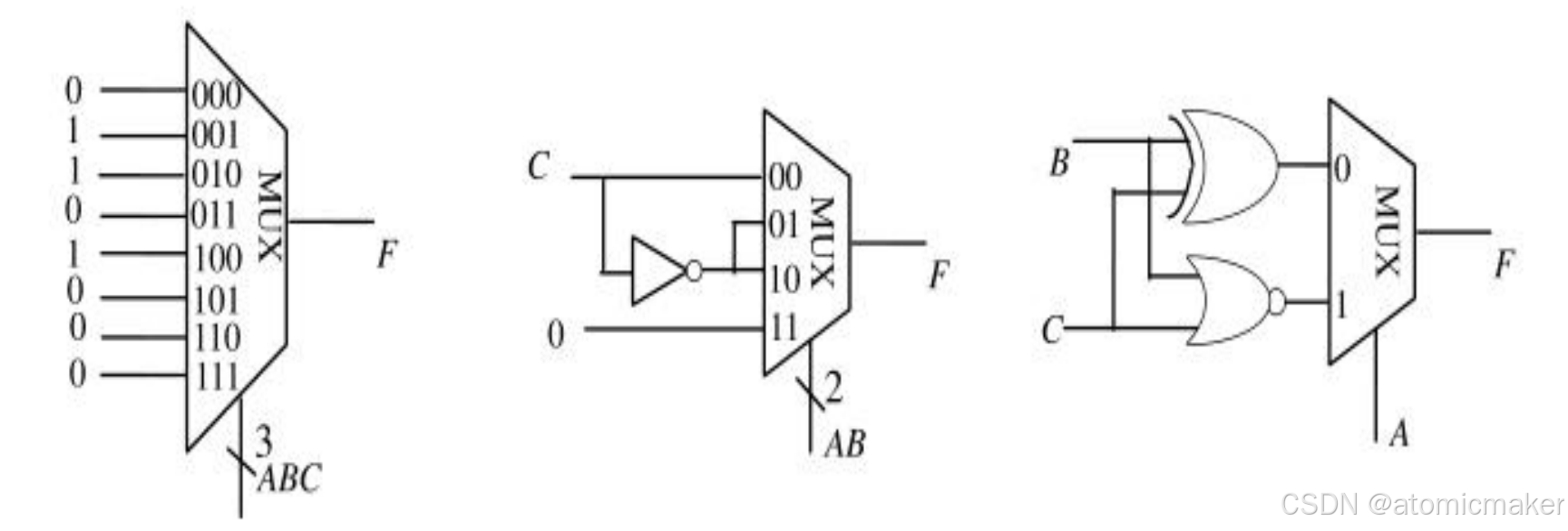
1)多路选择器
根据选择控制信号,从多路输入数据中选择一路输出,相当于 “数字开关”。

时序逻辑电路
时序逻辑电路概述
时序逻辑电路:组合逻辑电路 + 存储单元(存在反馈通路,这是与组合逻辑的本质区别)。
- 记忆性:包含存储单元(锁存器、触发器),用于保存电路的历史状态。
- 输入分类
- 逻辑输入:决定电路状态变化的条件。
- 时钟输入(CLK):控制存储单元状态更新的同步信号(同步时序电路特有)。
- 输出分类
- Moore 型:输出仅由当前状态决定,与输入无关。
- Mealy 型:输出由当前状态 + 当前输入共同决定。
锁存器和触发器
1.锁存器
电平触发的存储单元,状态更新由使能信号的电平控制:当使能信号有效时,锁存器的输出随输入变化(“透明” 状态);当使能信号无效时,输出保持当前状态不变。
1)SR 锁存器
原理图与符号
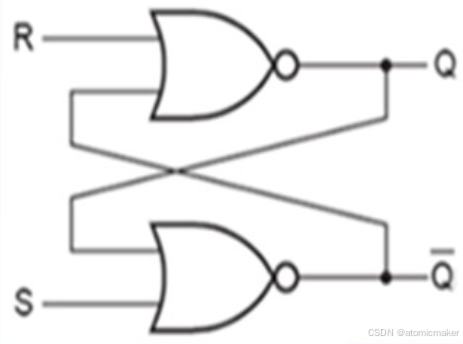
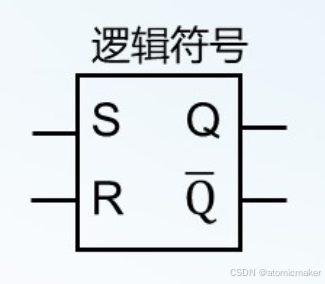
| 0 | 0 | 保持 | 保持 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 禁止 | 禁止 |
2)D 锁存器
原理图与符号

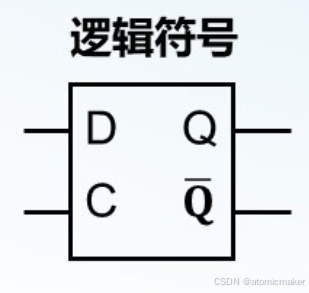
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| X | 0 | 状态不变 | 状态不变 |
2.触发器
1)D 触发器
原理图与符号:


| 0 | 上升 | 1 | 0 |
| 1 | 上升 | 0 | 1 |
| X | 0 | 状态不变 | 状态不变 |
| X | 1 | 状态不变 | 状态不变 |
同步时序逻辑设计
同步时序逻辑设计的真值表是由状态图得到的。
状态图的设计:
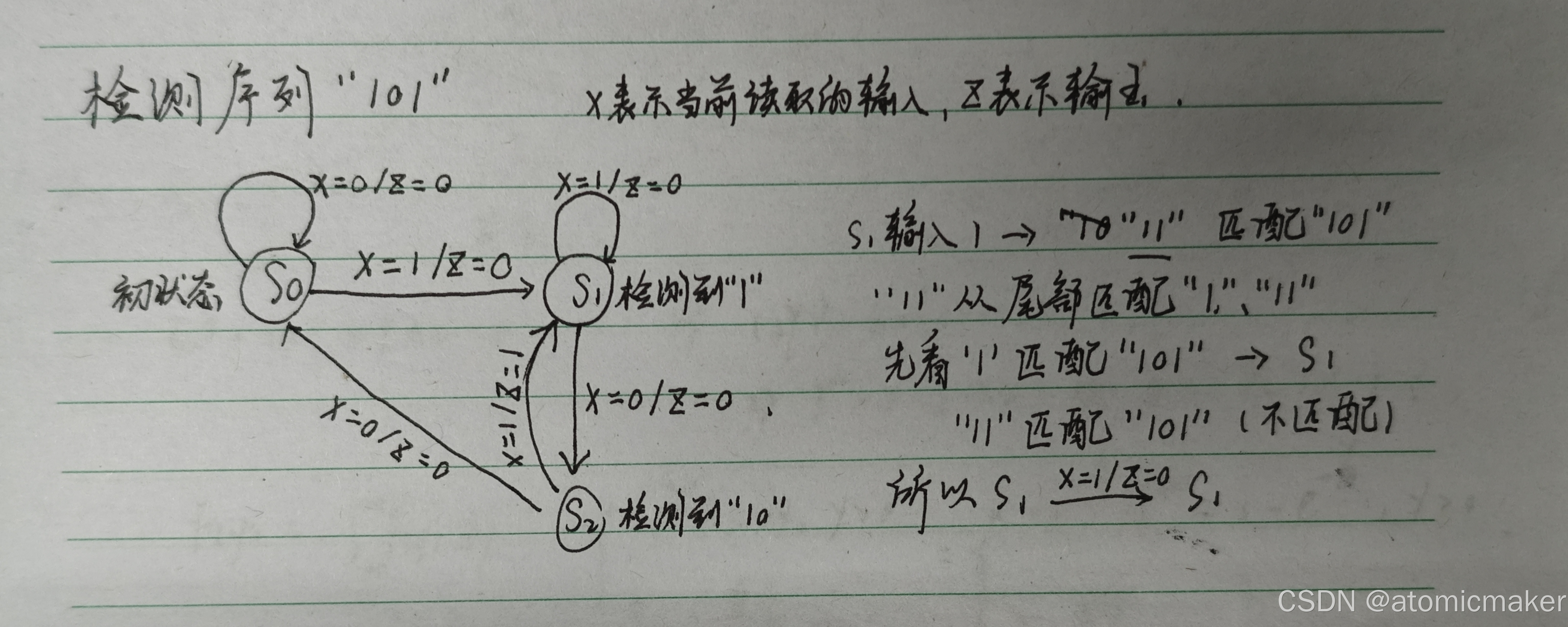
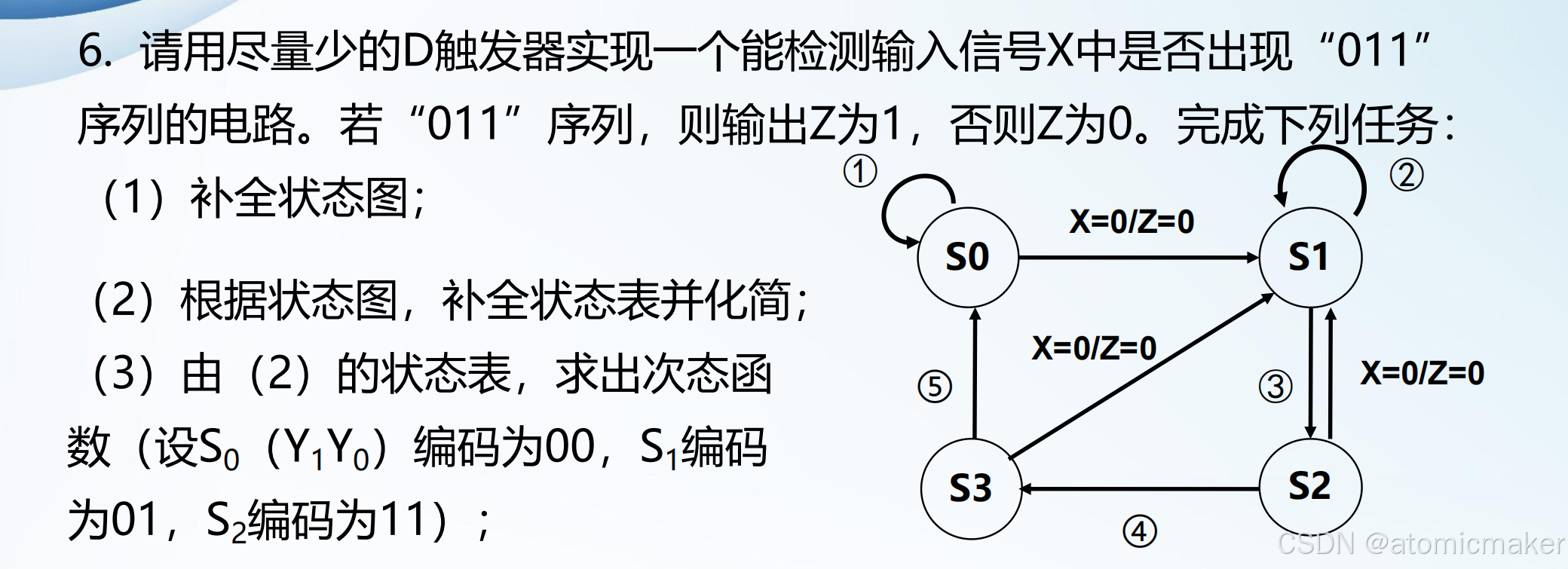
状态图:
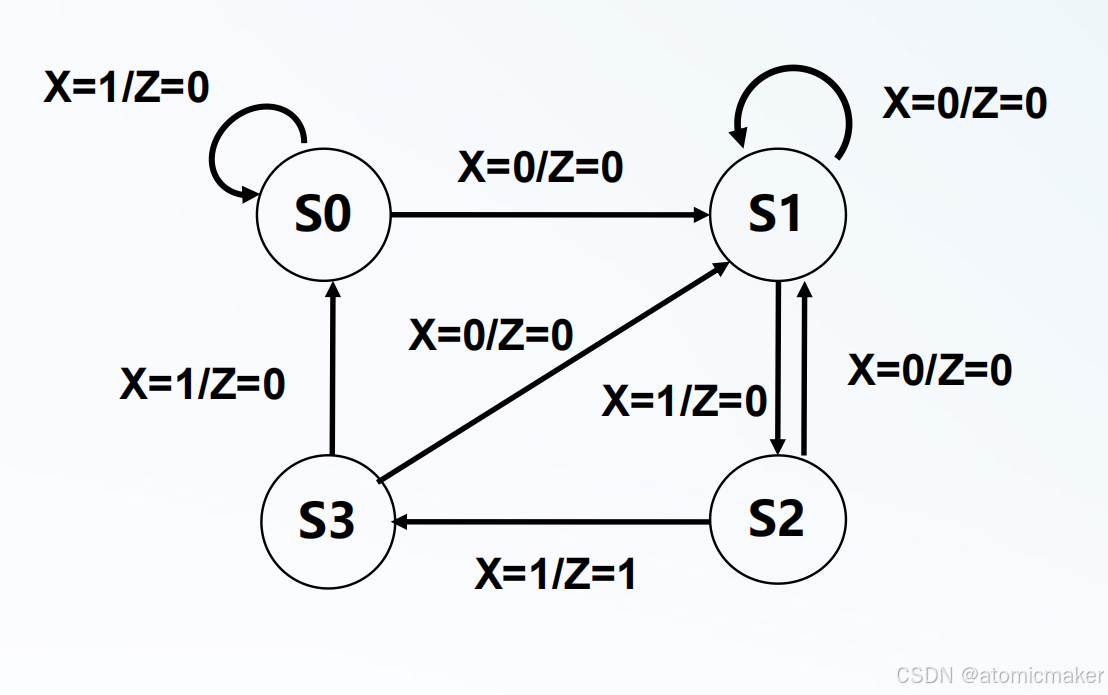
状态表:

由状态表得到状态转换表,再得到真值表,从而得到次态函数。
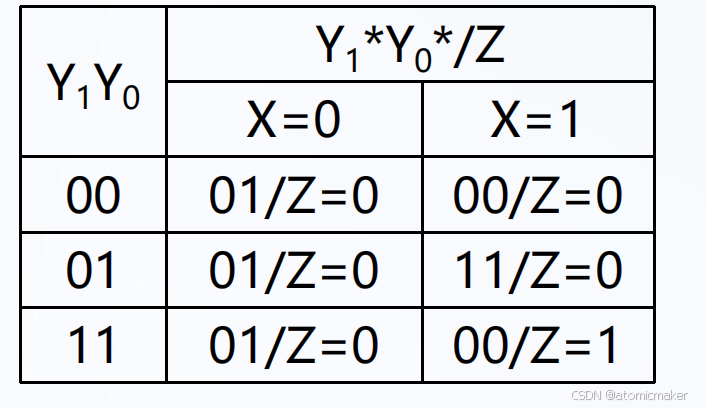
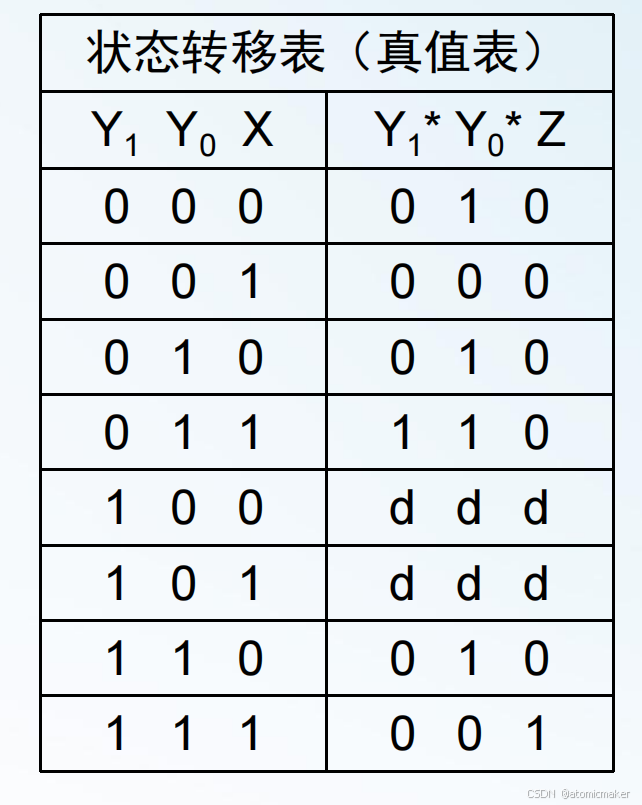





















 1804
1804

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








