离散数学——集合论

目录

集合等式证明

集合表示，集合基数计算

集合表示

集合基数计算

关系定义、性质，关系运算

关系定义

关系表示

关系性质

关系运算

偏序关系定义、哈斯图、特殊元素

偏序关系

哈斯图

偏序关系8种特殊元素

等价关系定义、等价类、划分

等价关系

等价类

商集

划分

函数定义、特殊函数、函数运算及函数性质证明

函数定义

函数判断

特殊函数

函数运算

---

集合等式证明

定理：对于任意两个集合A和B，A⊆B且B⊆A，当且仅当A=B。

集合表示，集合基数计算

集合表示

1. 枚举法：将集合中的元素全部列出，写在花括号内，元素之间用逗号隔开（{1, 2, 3}）。
2. 描述法：通过刻画集合中元素所具备的某种特性来表示集合（A={x | P(x)}）。
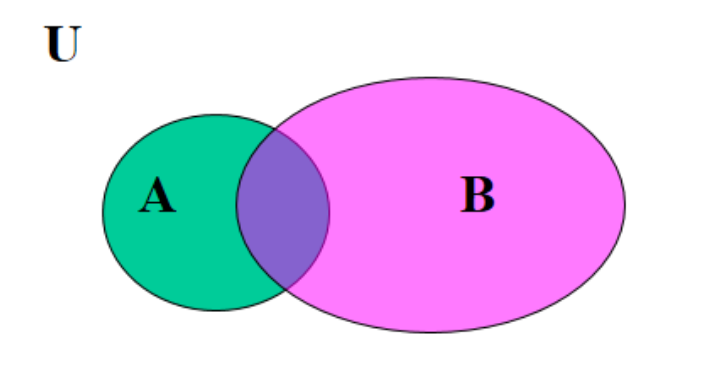
3. 图形法（文氏图法）：利用平面上点的对应元素的封闭区域对集合进行图解表示（一般通过方形或圆形表示一个集合）。

集合基数计算

基数：一个集合中的元素个数称为集合的基数（用 |A| 或 card(A) 表示）。

幂集：对于任意集合A，由A的所有不同子集为元素组成的集合称为A的幂集合，简称为幂集（用P(A) 或 2^A表示）。

        如果| A | = n，则 | P(A) | = 2^n 。

容斥原理：设A，B是有限集合，则：

                        | A U B | = | A | + | B | - | A ∩ B |

                  而对于有限集合A、B和C，AUBUC 的基数为：

                        | A U B U C | = | A | + | B | + | C | - | A ∩ B | - | A ∩ C| - | B ∩ C | + | A ∩ B ∩ C | 

因此可以得出容斥原理的推论

对于有限集合 Ai ( i = 1, 2, 3, 4 ... n)，其基数为：

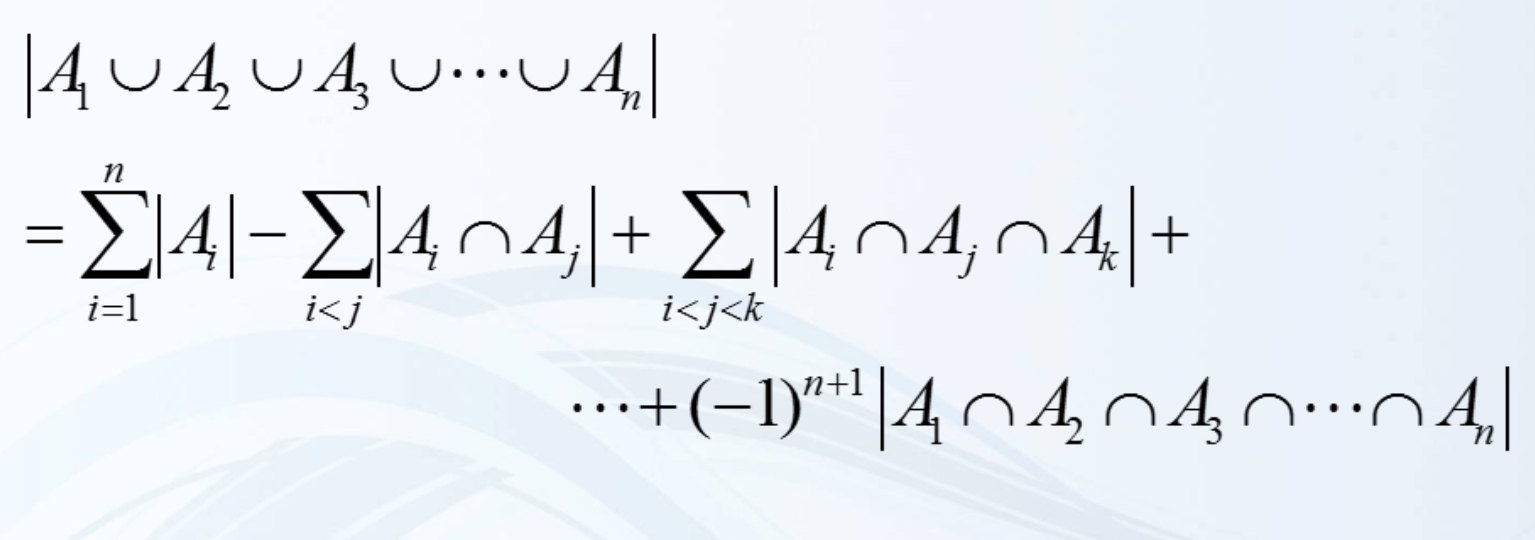
容斥原理的应用：

关系定义、性质，关系运算

关系定义

序偶

由两个元素x和y按照一定的次序排列成的二元组称为一个有序对或序偶，记为<x,y>。

其中，x称为序偶的第一元素或前元素，y称为序偶的第二元素或后元素。

两个序偶的前元素和后元素分别都相等时，才能称两个序偶相等。

笛卡尔积

对于集合A和B，以A中元素为第一元素，B中元素为第二元素组成序偶，所有这样的序偶组成的集合称为A和B的笛卡尔积，记作A×B：

A×B = {<x, y> | x ∈ A, y ∈ B }

关系

如果一个集合的全体元素都是序偶，则称这个集合为一个二元关系，简称为关系，记作R。

对于某个二元关系R，若<x, y> ∈ R，则称x与y以R相关，也常记为xRy。

设A、B为任意集合，将A×B的任一子集R称为集合A到集合B的一个关系（当A = B时，称R为A上的关系）。

常见特殊关系

空关系：对于非空集合A，空集∅称为A上的空关系。

全域关系：关系Ea = { <x, y> | x ∈ A, y ∈ A } 。

恒等关系：关系Ia = { <x, x> | x ∈ A }。

等价关系：见下文。

偏序关系：见下文。

关系表示

1.集合法

上面对关系的定义就是用集合表示关系的，一般常用集合表示。

例题：

2.关系图

简单来说就是序偶 <x, y> 由 x 指向 y。

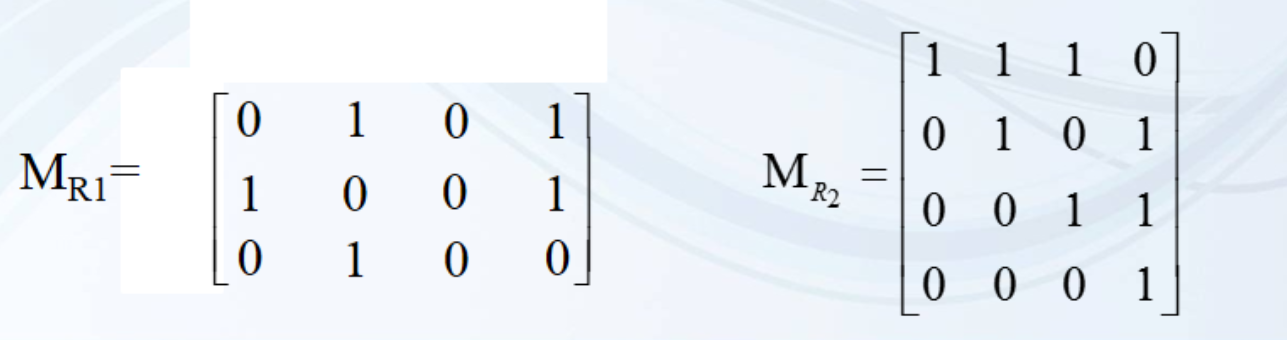
3.关系矩阵

<x, y>存在，则点(x, y)为1，否则为0。

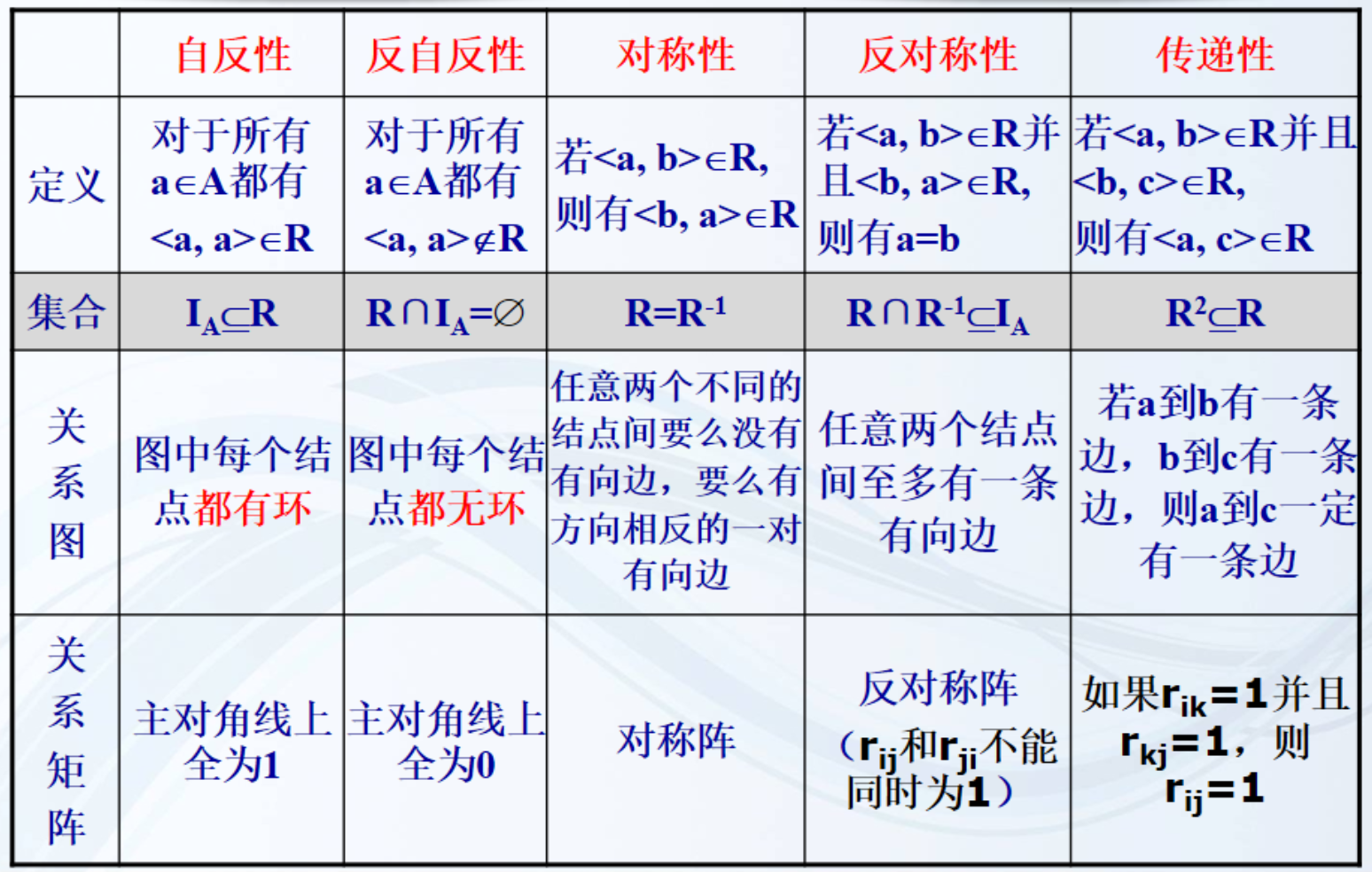
关系性质

大家根据定义判断比较方便

关系运算

基本运算（集合运算）：并、交、差、补、对称差。（关系是一种集合，集合的所有基本运算都使用与关系）

特殊运算：复合运算、逆运算、幂运算、闭包运算。

复合运算

        设R是一个从集合A到集合B的关系，S是从集合B到集合C的关系，则定义关系R和S的复合关系为集合A到集合C的关系。（类似传递）

逆运算

        设R是一个集合A到集合B的关系，则定义关系R的逆关系为集合B到集合A的关系。

幂运算

        设R是一个集合A上的关系，n为自然数，则，关系R的n次幂（R的n次幂就是n次个R的复合）定义为：

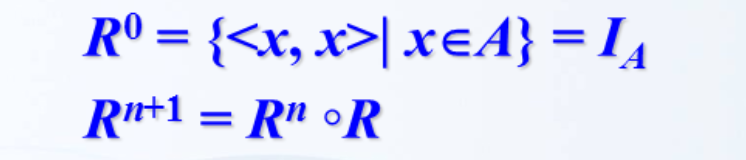
闭包运算

闭包运算分为自反闭包（ r(R) ）、对称闭包 ( s(R) )、传递闭包 ( t(R) )

实际上就是对集合上的关系，添加最少的元素，使其具有相关的性质。

例如：

自反闭包

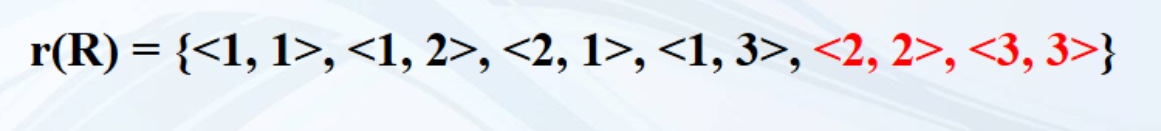
添加了<2, 2>，<3, 3>，用最少的元素使其满足自反性。

对称闭包

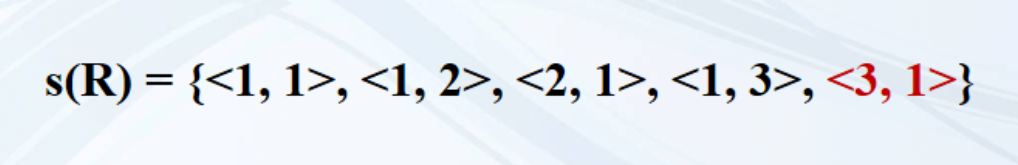
添加了元素<3, 1>，使得新关系s(R)具有对称性。

偏序关系定义、哈斯图、特殊元素

偏序关系

对于非空集合A上的二元关系R，如果R是自反的，反对称的和传递的，则称R为A上的偏序关系；

简称偏序，记为 "≤"，并将序偶 <x, y> ∈ R记为 x ≤ y。

注意：这里的 "≤" 不是数值的大小，而是在偏序关系中的顺序性。x ≤ y 的含义是：依照这个序，x在偏序上排在y的前面或相同。

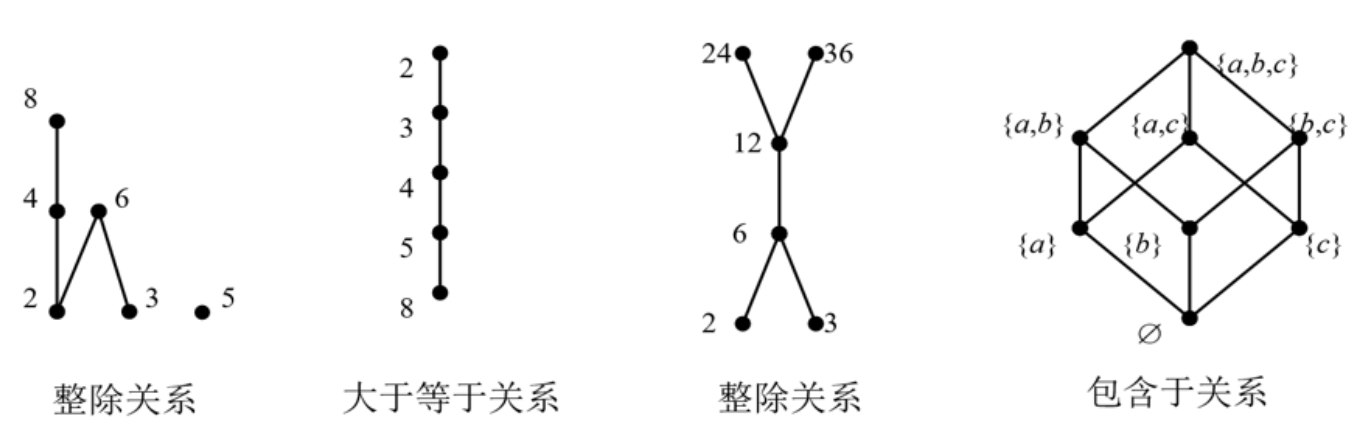
哈斯图

可比、不可比、盖住定义

设R为非空集合A上的偏序关系，对于任意元素x, y ∈ A，

• 若 x ≤ y 或者 y ≤ x，则称 x 与 y 是可比的；
• 若 x ≤ y 且 x ≠ y，则称 x 排在 y 的前面，记 x < y；
• 若 <x, y> ∉ R 且 <y, x> ∉ R，则称 x 与 y 是不可比的；
• 若 x < y 且不存在元素 z ∈ A，使得 x < z 且 z < y，则称 y 盖住 x。

绘制步骤

1. 以 "·" 表示元素；
2. 若 x < y，则 y 画在 x 的上层；
3. 若 y 盖住 x，则连线；
4. 不可比的元素可画在同一层。

例子：

偏序关系8种特殊元素

大家根据核心特征进行判断比较容易懂。

特殊元素类型	定义（设偏序集为⟨A, ≤⟩，x∈A）	核心特征	关键说明
最大元	对所有 a∈A，都有 a ≤ x	能 “大于等于” 集合 A 中所有元素，若存在则唯一	需覆盖整个集合，不存在比它更大的元素；与极大元的区别是 “全局支配” 而非 “局部无更大”
最小元	对所有 a∈A，都有 x ≤ a	能 “小于等于” 集合 A 中所有元素，若存在则唯一	需覆盖整个集合，不存在比它更小的元素；与极小元的区别是 “全局被支配” 而非 “局部无更小”
极大元	不存在 a∈A，使得 x ≤ a 且 x ≠ a	集合 A 中没有比它更大的元素（局部顶端），可能不唯一	无需支配所有元素，仅自身无 “上界”；若存在最大元，则最大元是唯一的极大元
极小元	不存在 a∈A，使得 a ≤ x 且 x ≠ a	集合 A 中没有比它更小的元素（局部底端），可能不唯一	无需被所有元素支配，仅自身无 “下界”；若存在最小元，则最小元是唯一的极小元
上界	对所有 a∈A，都有 a ≤ x（x 可∈A，也可∉A）	能 “大于等于” 集合 A 中 所有元素，允许在集合A外，可能不唯一	范围比最大元广（最大元是属于 A 的上界）；多个上界中可能存在 “最小的上界”（上确界）
下界	对所有 a∈A，都有 x ≤ a（x 可∈A，也可∉A）	能 “小于等于” 集合 A 中 所有元素，允许在集合A外，可能不唯一	范围比最小元广（最小元是属于 A 的下界）；多个下界中可能存在 “最大的下界”（下确界）
上确界	x 是 A 的所有上界中最小的那个（即 x 是上界，且对 A 的任一上界 y，都有 x ≤ y）	是所有上界的最小元，若存在则唯一；必须满足 “最小性”	上确界可能属于 A（此时即为最大元），也可能不属于 A；无界的集合不存在上确界
下确界	x 是 A 的所有下界中最大的那个（即 x 是下界，且对 A 的任一下界 y，都有 y ≤ x）	是所有下界的最大元，若存在则唯一；必须满足 “最大性”	下确界可能属于 A（此时即为最小元），也可能不属于 A；无界的集合不存在下确界

例如：

集合A = {e1, e2, e3, e4, e5, e6, e7}。

偏序关系和哈斯图如下 ，

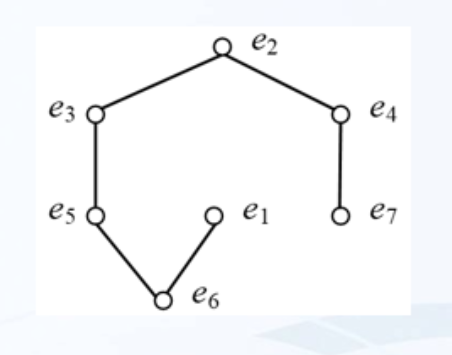
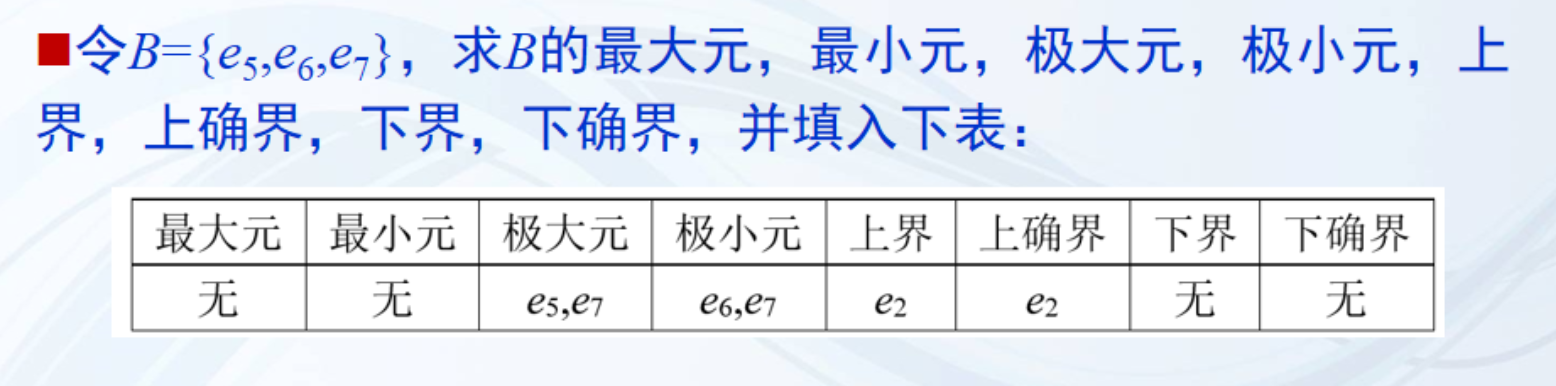
等价关系定义、等价类、划分

等价关系

设R为非空集合A上的关系（即A≠∅且R⊆A×A），如果R是自反的、对称的和传递的，则称R为A上的等价关系。

设R是一个等价关系，若<x, y>∈R，则称x与y等价。

等价类

设R是非空集合A上的等价关系，对任意x∈A，称集合

为x关于R的等价类。（其中x为[x]的生成元或代表元）

例题：

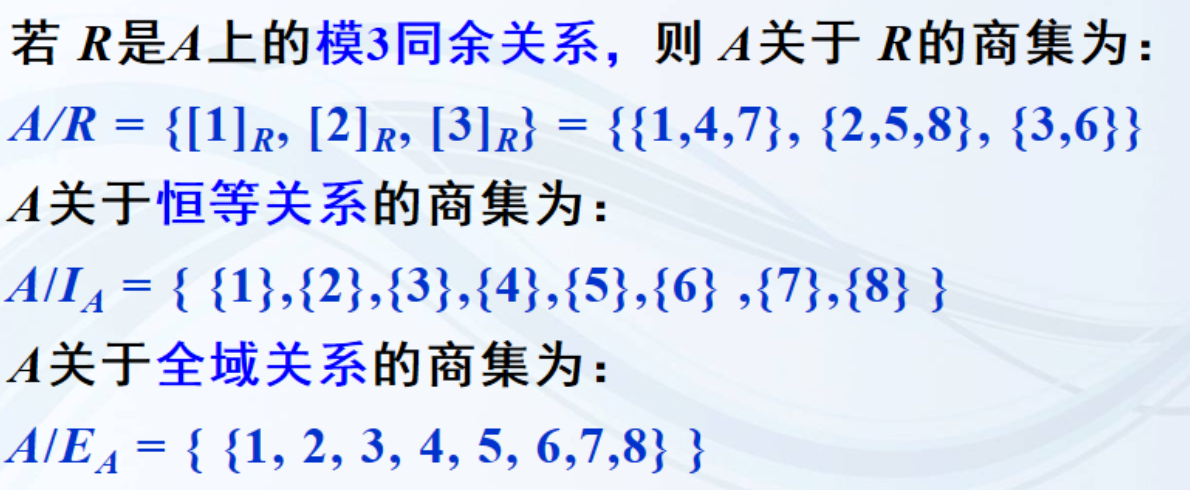
设R是集合A = {1, 2, 3, 4, 5, 6, 7, 8}上的模3同余关系，试用关系图表示该关系？并求R的所有等价类。

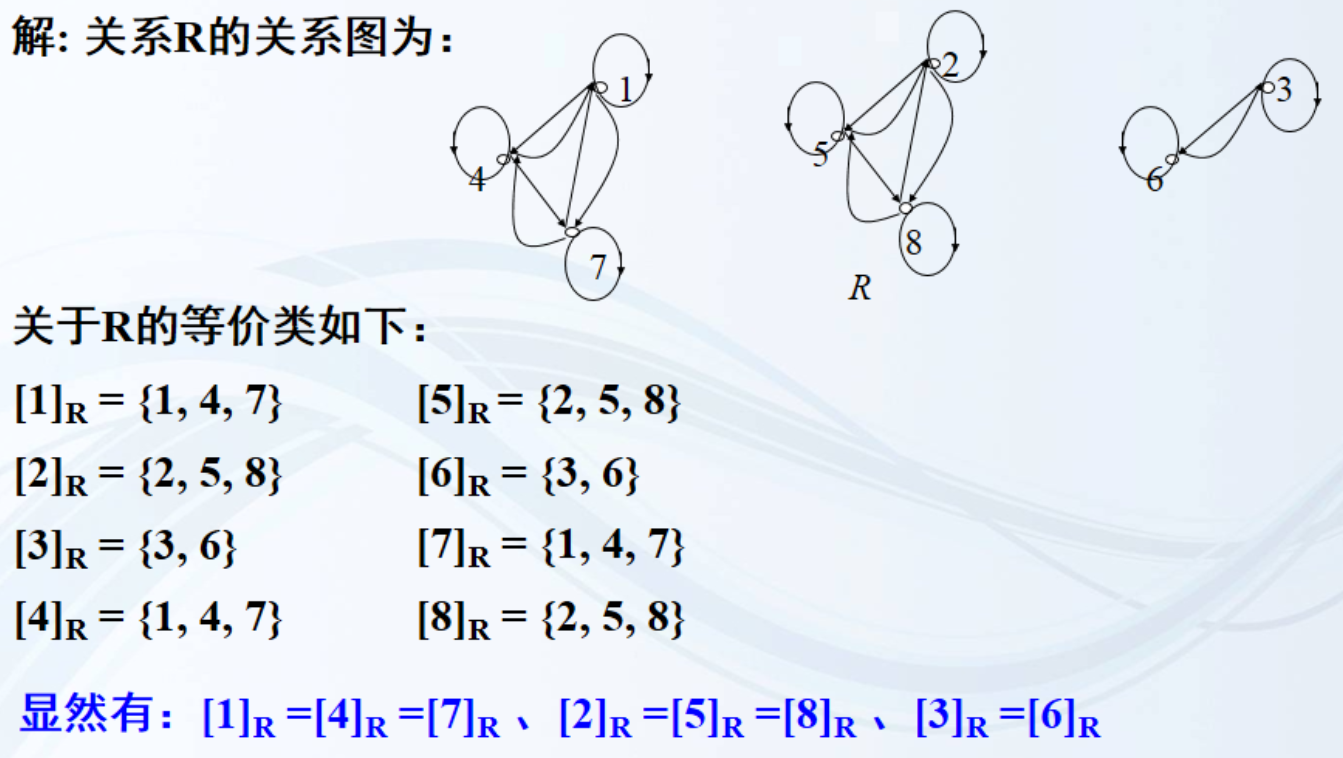
对于任意x, y∈A，如果<x, y>∈R，则[x] = [y]。

商集

设R是非空集合A上的等价关系；将由R的所有等价类构成的集合称为A关于R的商集，记作A/R。

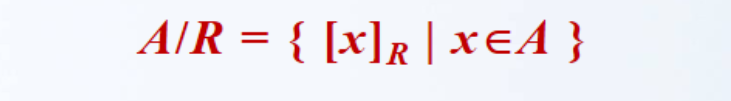
例子：

集合 A = {1, 2, 3, 4, 5, 6, 7, 8}。

划分

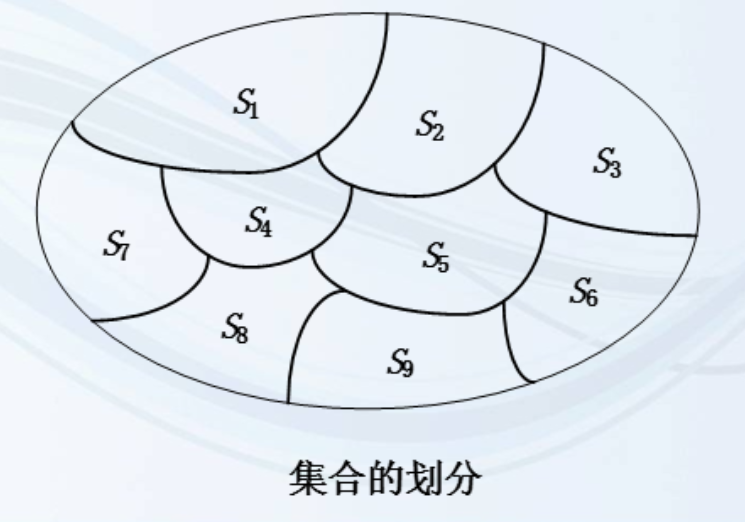
对于非空集合A，S={S1, S2, ... , Sm}如果满足

1. Si ⊆ A 且 Si ≠ ∅ （i=1, 2, ..., m），
2. Si ∩ Sj = ∅（i ≠ j; i = 1, 2, ..., m; j = 1, 2, ..., m），
3. S1 ∪ S2 ∪ ... ∪ Sm = A

则称S为A的一个划分，而S1，S2，...，Sm分别称为这划分的块或类。

等价类、商集与划分：

设R是非空集合A上的等价关系，则集合A上关于R的商集A/R是A的一个划分。（称之为由等价关系R导出的等价划分）

每个等价类都是一个划分块。

设{S1, S2, ..., Sm}是非空集合A的一个划分，则由该划分确定的关系

        R = (S1 × S1) ∪ (S2 × S2) ∪ ... ∪ (Sm × Sm)

是A上的等价关系，称之为由该划分所导出的等价关系。

例题：设集合A = {1, 2, 3, 4, 5}。

关系求划分

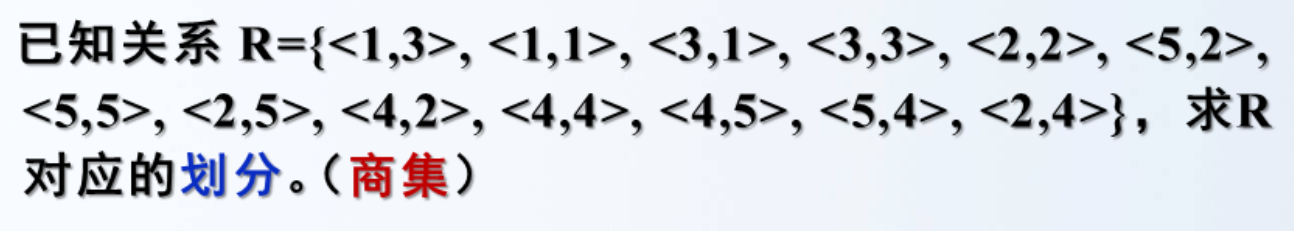
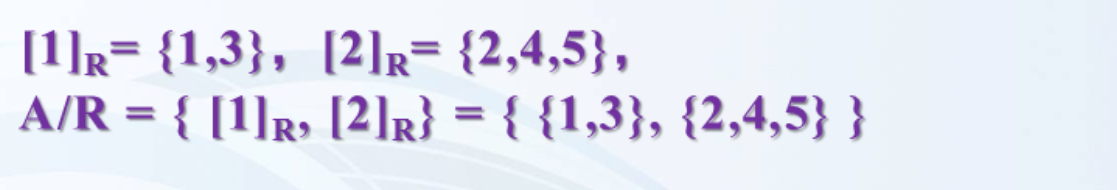
划分求关系

函数定义、特殊函数、函数运算及函数性质证明

函数定义

设f是集合A到B的关系，如果对每个 x∈A ，都存在唯一的 y∈B 使得 <x, y>∈f，则称关系 f 为集合A到集合B的函数或映射，记为 f: A -> B 或 y = f(x)。

其中x为函数 f 的自变量或源点，y为x在函数 f 下的函数值或像点。

集合A称为函数 f 的定义域，记为dom f = A。所有像点组成的集合称为函数f的值域或函数f的像，记为ran f 或 f(A)

函数是一种特殊的关系，它要求A中每一个元素都与B中元素相关。

函数判断

1. 定义域是集合A，而不能是集合A的任意一个真子集。
2. 对于定义域中的任意一个元素都有唯一的值和其对应，也就是说只能是多对一，而不能是一对多，称之为像点的单值性。
3. 集合A到B的函数 f 的值域 f(A) 是集合B的子集，即f(A) ⊆ B。
4. f(x)表示一个函数值，f是一个序偶的集合，因此f(x) ≠ f。

例子：

判断下列关系那些是函数？

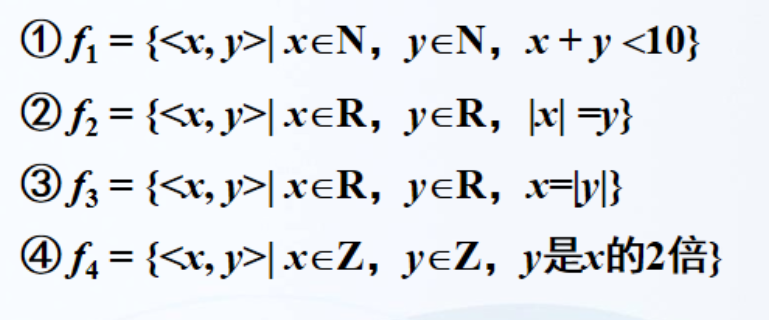
特殊函数

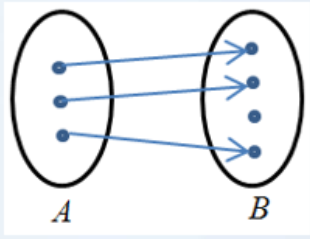
1.单射函数

设 f 是 集合A 到 B 的函数，对于A中任意两个元素 x 和 y，如果 x ≠ y 时，都有 f(x) ≠ f(y) ，则称f是集合A到B的单射函数或一对一的映射。

必要条件：|A| ≤ |B|

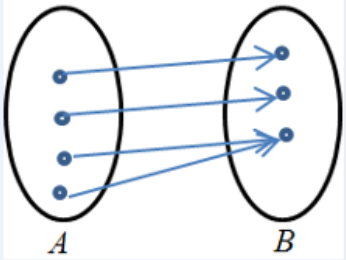
2.满射函数

设 f 是 集合A 到 B 的函数，如果函数f的值域恰好是集合B，即f(A) = B，则称f是集合A到B的满射函数或A到B上的映射。

必要条件：|B| ≤ |A|

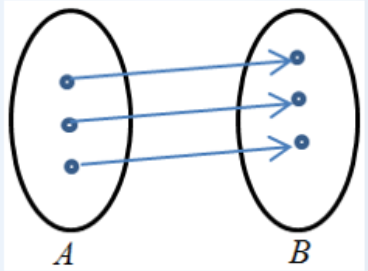
3.双射函数

设f是集合A到B的函数，如果函数f既是集合A到B的单射函数，又是集合A到B的满射函数，则称f是集合A到B的双射函数或一一对应的映射。

必要条件：|A| = |B|

函数运算

复合运算

对于集合A到B的函数f和集合B到C的函数g，复合关系 f∘g 称为函数f和函数g的复合函数，记为f∘g: A -> C。（"∘"为函数的复合运算）

注意：<x, z> ∈ f∘g 是指存在 y 使得 <x, y> ∈ f 和 <y, z> ∈ g，即 y = f(x)，z = g(y)，f∘g(x) = g(f(x))。(f∘g 是函数，f∘g(x)是变量x的函数值)

例子：

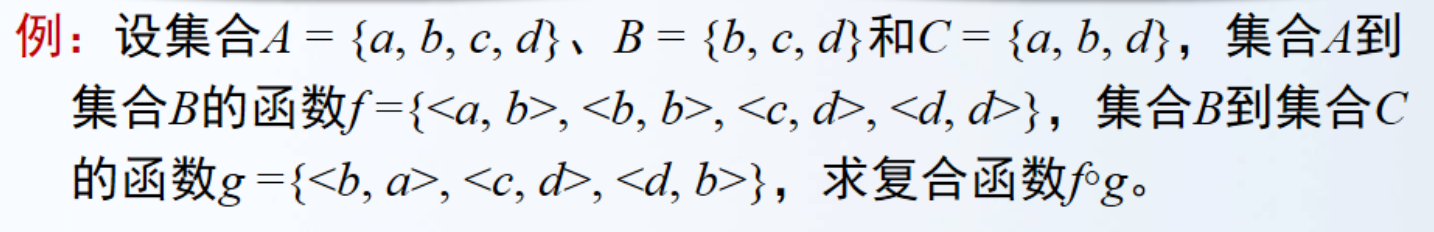
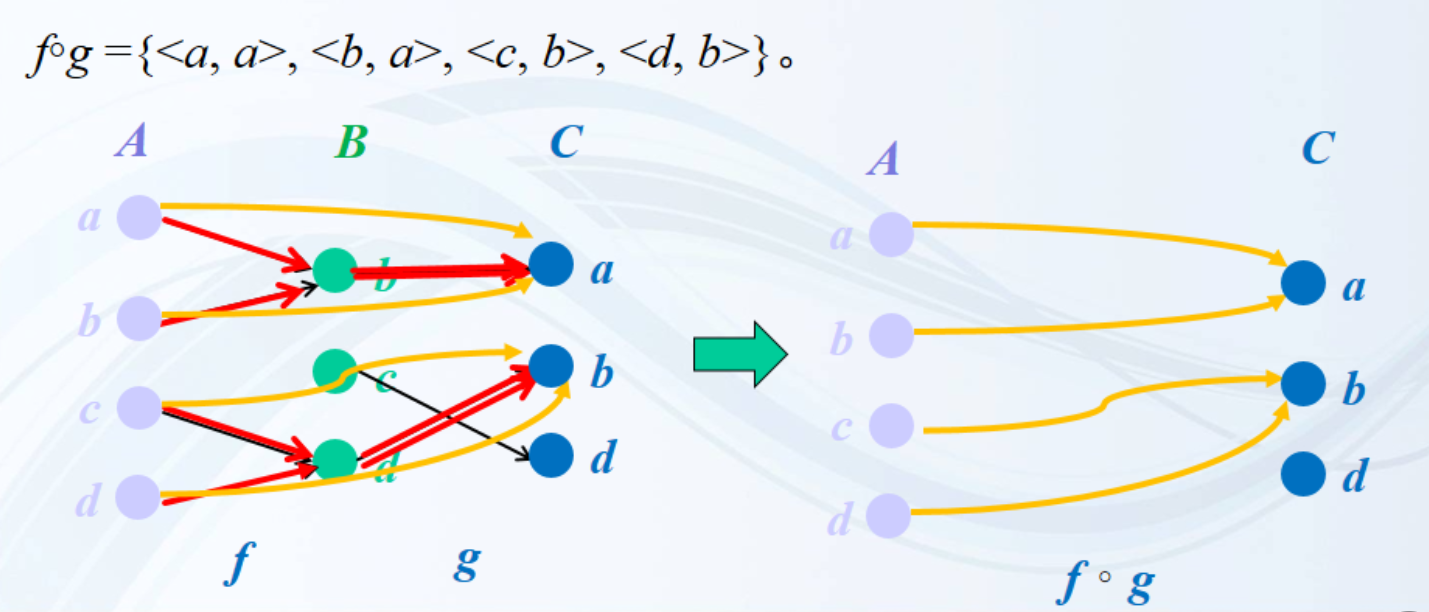
相关性质

1. 若f 和 g 都是单射/满射/双射，则f∘g也是单射/满射/双射。
2. 若 f∘g 是单射，则f是单射，但g不一定是单射。
3. 若 f∘g 是满射，则g是满射，但f不一定是满射。
4. 若 f∘g 是双射，则f是单射，g是满射。

逆运算

对于集合A到B的关系g，如果关系g是A到B函数且其逆关系g^-1是B到A函数，那么称g^-1是函数g的逆函数或反函数，记为g^-1: B -> A。并称 "-1" 为函数的逆运算。

如果g是集合A到B的双射函数，则g的逆关系g^-1是集合B到A的函数（即一定存在逆函数）。

例子：

逆函数的求法：

遵循 “反解变量 → 互换变量 → 确定定义域” 的流程：

1. 反解变量：从原函数 y = f(x) 中，把 x 用 y 表示出来（即解关于 x 的方程）；
2. 互换变量：将 x 和 y 互换，得到 y = f^-1(x)（符合自变量用 x 表示的习惯）；
3. 确定定义域：逆函数的定义域 = 原函数的值域，需明确标注（避免定义域错误）。

可以通过f(f^-1(x)) = x验证逆函数是否正确。

集合论的旅途到这里就要结束了，接下来还会有命题逻辑与图论。没点关注的点点赞，没点赞的点点收藏，没点收藏的点点关注，我们下次再见。