二分查找算法详解与应用
问题引入
给一个有序数组，返回第一个 >= 8 的数的位置，如果所有数都 < 8 ，返回数组长度。
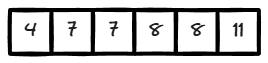
暴力做法：遍历每个数，判断是否 >= 8 ?（ 时间复杂度 O(n) ）
不难看出，暴力做法没有用到数组有序这个条件，那如何去运用这个条件呢。
我之前讲过，双指针可以用于遍历有序数组（没看过的可以先去看一下我之前写的文章经典算法——相向双指针），同样，这边我们也可以使用双指针去遍历。
高效做法：
红蓝染色法（博主是从灵神那学来的 二分查找 红蓝染色法【基础算法精讲 04】_哔哩哔哩_bilibili讲的实在太好了，大家要是不想看文章可以直接去看他的视频。大家看完了可以再回来看看，复习一下，后面有稍微的补充）
开始判断：
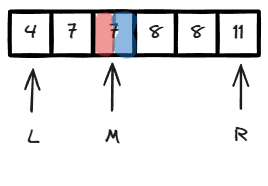
用双指针，L和R分别指向询问的左右边界，M（L和R取中值，二分的核心思想）指向当前正在询问的数。
红色背景表示 false，即 < 8
蓝色背景表示 true，即 >= 8
白色背景表示不确定
判断结果：
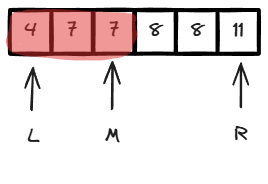
M是红色（判断M是什么颜色）-> [L，M] 都是红色（有序数组，双指针思想）
剩余不确定的区间为 [M + 1, R]
因此下一步 L <- M + 1（同时表明，L - 1 指向的一定是红色）
判断与结果：
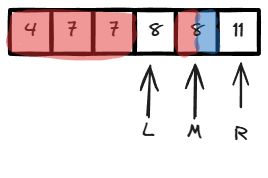
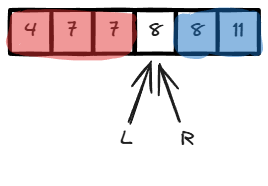
M是蓝色 -> [M, R] 都是蓝色
剩余不确定的区间为 [L, M-1]
因此下一步 R <- M - 1 （同时表明，R + 1 指向的一定是蓝色）
判断与结果
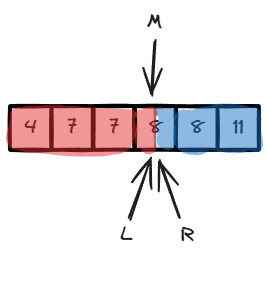
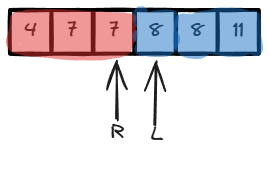
关键：循环不变量
L - 1始终是红色
R + 1始终是蓝色
根据循环不变量，R + 1就是我们的答案
由于循环结束后 R + 1 = L
所以答案也可以用 L 表示
算法模版
红蓝染色法版
灵活多变，可以自己根据题目来调整具体函数。
总结一些常见变种：
>= target（初始函数）
> target（ 可以转变成 >= target+1，即 lower_bound(nums, target+1) )
< target（可以转变成 (>= target)-1，即 lower_bound(nums, target)-1 ）
<= target（可以转变成 (> target)-1, 即 lower_bound(nums, target+1)-1 ）
//nums非递减，即 nums[i] <= nums[i+1]
//返回最小的满足 nums[i] >= target 的 i，不存在则返回 nums.size()
int lower_bound(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; //闭区间 [left, right]
while (left <= right) { //区间不为空
int mid = (left + right) / 2;
//防止溢出：left + (right - left) / 2;
//red：< target，blue：>= target
//所要求的就是 blue
if (nums[mid] < target) { //mid isred
left = mid + 1; //[mid+1, right]
}
else { //mid isblue
right = mid - 1; //[left, mid-1]
}
}
//循环不变量 right + 1 始终为 blue (>= target)
return left; //right + 1 = left
}C++ STL模版函数
lower_bound 返回第一个 大于等于 给定值的元素位置。如果目标值不存在，则返回第一个大于目标值的元素位置；如果元素均小于目标值，则返回 v.end()。
upper_bound 返回第一个 大于 给定值的元素位置。如果目标值不存在，则行为与 lower_bound 类似。
#include <bits/stdc++.h>
using namespace std;
int main() {
vector<int> v = {1, 2, 4, 4, 5};
auto it = lower_bound(v.begin(), v.end(), 4); //大于等于 4
cout << "lower_bound 位置: " << (it - v.begin()) << ", 值: " << *it << endl;
//lower_bound 位置: 2, 值: 4
it = upper_bound(v.begin(), v.end(), 4); //大于 4
cout << "upper_bound 位置: " << (it - v.begin()) << ", 值: " << *it << endl;
//upper_bound 位置: 4, 值: 5
//当元素不存在时（即没有大于等于 target，或没有大于target的元素），lower_bound() 与 upper_bound 均返回的是 v.end()
//可用与查找元素是否存在
int target = 6;
bool exists = (lower_bound(v.begin(), v.end(), target) != v.end() && (*it == target)); //false
}算法应用
二分模版
二分查找，套用上面的算法模版就行，大家分别用红蓝染色和STL模版写一遍，一定要自己写，代码我就不放出来了。
二分查找特殊数组
二分查找一般只能用于有序数组，但遇到某些特殊数组时也能很好的使用。
比如下面这道题，
虽然跟一般的二分查找有序数组不一样，但我们同样可以使用红蓝染色法，查找target。
有序数组的 ＜ target 本质上就是在 target 的左边，≥ target 本质上是在 target 的右边（包括target），所以我们这里同样的道理，判断是在target左边还是右边。
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
int l = 0, r = n - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
int cur = nums[mid];
//红蓝染色法
//红:cur在target左边; 蓝:cur在target右边(包括target)
if (isred(nums, target, cur)) l = mid + 1;
else r = mid - 1;
}
if (l == n || nums[l] !=target) return -1;
else return l;
}
bool isred(vector<int>& nums, int target, int cur) {
//分类讨论，当target < nums[0](第一个元素时)，表示target在数组的右半边
if (target < nums[0]) {
/*
当target在数组的右半边时，判断cur是否在target的左边
也分为两种，
即cur在数组的右半边（cur < target表示在target的左边）
或左半边（需要cur满足在左半边的条件，而左半边肯定是在target的左边的）
*/
return cur < target || cur >= nums[0];
}
else {
//跟上面的同一道理
return cur < target && cur >= nums[0];
}
}
};下面这道也是特殊数组
852. 山脉数组的峰顶索引
https://leetcode.cn/problems/peak-index-in-a-mountain-array/description/
我们依旧红蓝染色法yyds，题目没有明确给出target，但给出了判断在target左边还是右边的方法，由于arr是一个山脉数组，所以，target左边的元素，a[i] < a[i+1]，在target右边的元素，a[i] > a[i+1]，那么题目就已经做完了。
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int n = arr.size();
//峰值的索引范围
int l = 1, r = n - 2;
while (l <= r) {
int mid = l + (r - l) / 2;
//isred 表示查询的元素在峰值的左边
if (arr[mid] > arr[mid-1]) l = mid + 1;
else r = mid-1;
}
//循环不变量
return r;
}
};对答案进行二分
对答案的范围进行二分查找，再判断是否符合条件。（关键词：最多、最少）
P1843 奶牛晒衣服https://www.luogu.com.cn/problem/P1843
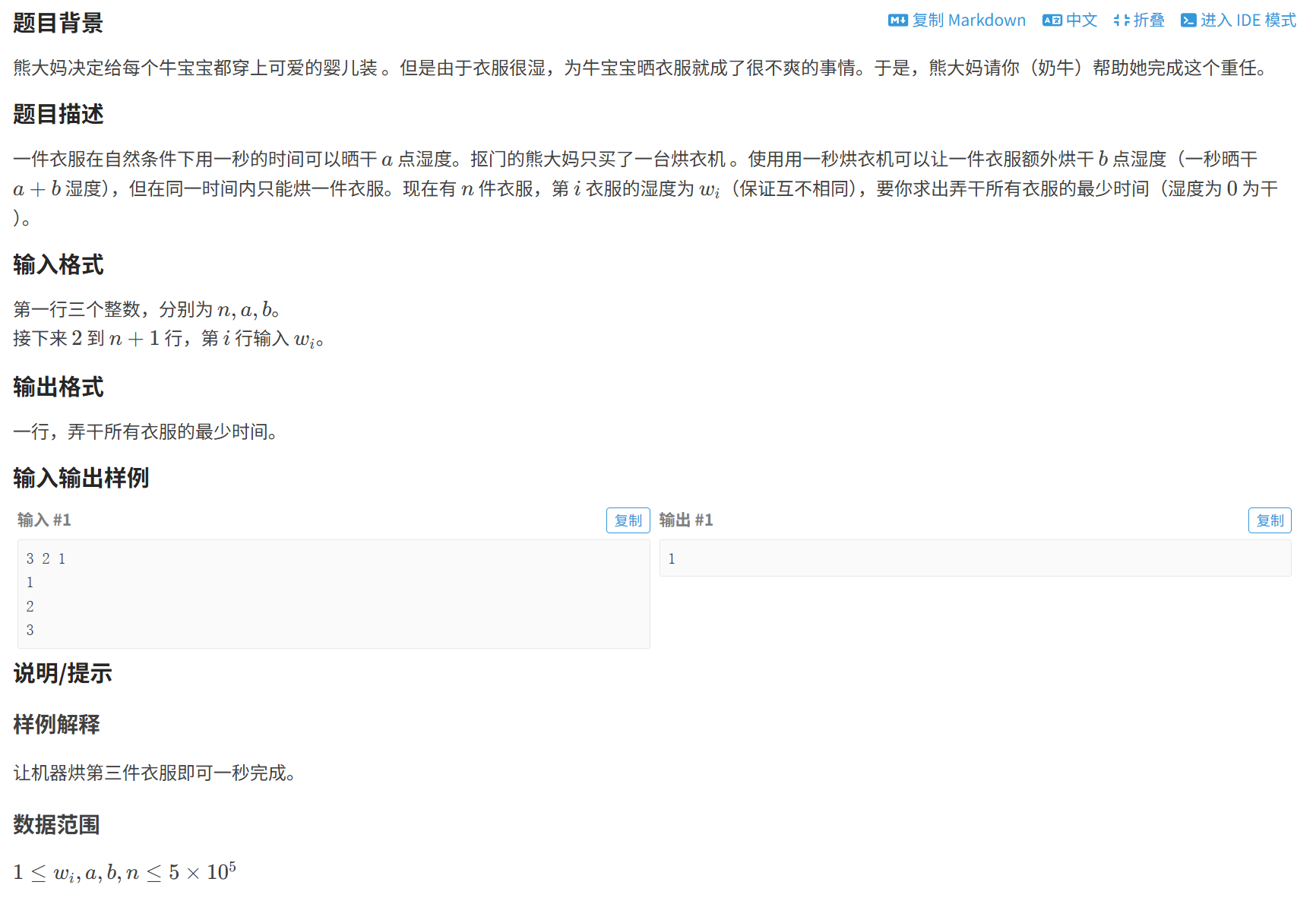
二分查找晒干所需的时间，再判断是否满足使用洗衣机的条件。
#include <bits/stdc++.h>
using namespace std;
int n, a, b;
bool isred(int t, vector<int>& w) {
//使用洗衣机的时间
int cnt = 0;
for (int i = 0; i < n; i++) {
int tmp = w[i];
//自然晒干外额外需要处理的湿度
int extra = tmp - t*a;
if (extra <= 0) continue; //不需要使用洗衣机
else {
//计算每件衣服需使用洗衣机的时间
cnt += extra / b + (extra % b != 0);
}
}
//使用洗衣机的时间超过最小时间，表示不能晒干
return cnt > t;
}
int main() {
cin >> n >> a >> b;
vector<int> w(n);
int l = 0, r = 0;
for (int i = 0; i < n; i++) {
cin >> w[i];
//衣服最大湿度
r = max(w[i], r);
}
//弄干衣服的最大时间
r = r / a + 1;
//红蓝染色法：红色->在时间mid不能晒干
while (l <= r) {
int mid = l + (r - l) / 2;
if (isred(mid, w)) {
l = mid + 1; //l-1 时间内不能晒干
}
else {
r = mid - 1;//r+1 时间内都能晒干
}
}
//r+1 = l （循环不变量，r+1时间能晒干）
cout << l << endl;
}下面我再给一些类似这样的题目，只要懂了一个写法都是一样的，只不过是判断不一样而已。
大家自己去写一写练练手，如果有需要的话可以评论一下，我再补充代码。
1482. 制作 m 束花所需的最少天数 - 力扣（LeetCode）
2064. 分配给商店的最多商品的最小值 - 力扣（LeetCode）
2187. 完成旅途的最少时间 - 力扣（LeetCode）
2226. 每个小孩最多能分到多少糖果 - 力扣（LeetCode）
ps：没点关注的点点关注，没点赞的点点赞，没点收藏的点点收藏，我们下期再见。
扫一扫
1946
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
