目录
大家如果想要学习将图运用到实际算法代码中可以去看看我写的文章数据结构与基础算法——图(一篇讲透)-优快云博客,本篇讲的是离散数学中的图,不涉及代码实现的理论,如果对图不了解的可以先看看这篇(当然,想要复习离散数学的也进来看看)。
图的概念
大家在做图的题目时,如果可以画出来整个图就尽量画出来,就用点和线表示结点和边。
图的定义
结点集合V = {v1, v2, ... , vn}和连接结点的边集合E = {e1, e2, ... , em} 组成的二元组G = <V, E> 称为图。图中的结点集合的基数n称为图的阶数,即n阶图,或者(n, m)图。
相关定义
无序序偶:两个元素x和y无序排列成的二元组称为一个无序对或无序序偶,记作(x, y)。
无序积:对于集合A和B,集合A中元素和集合B中元素组成的无序序偶的集合称为A和B的无序积,记作A&B,形式化表示为A&B = { (x, y) | x∈A, y∈B }。
有向边:从结点u到结点v的有方向的边,用<u, v>表示。
无向边:从结点u到结点v的无方向的边,用无序序偶(u, v)表示。
自环:从结点u到结点u的边。
关联边:以结点u为端点的边,成为结点u的关联边。
平行边(重复边):在结点u和结点v之间,具有相同始点和相同终点的多条有向边,或者连接结点u到结点v的多条无向边,并称平行边(重复边)的条数为边的重数。
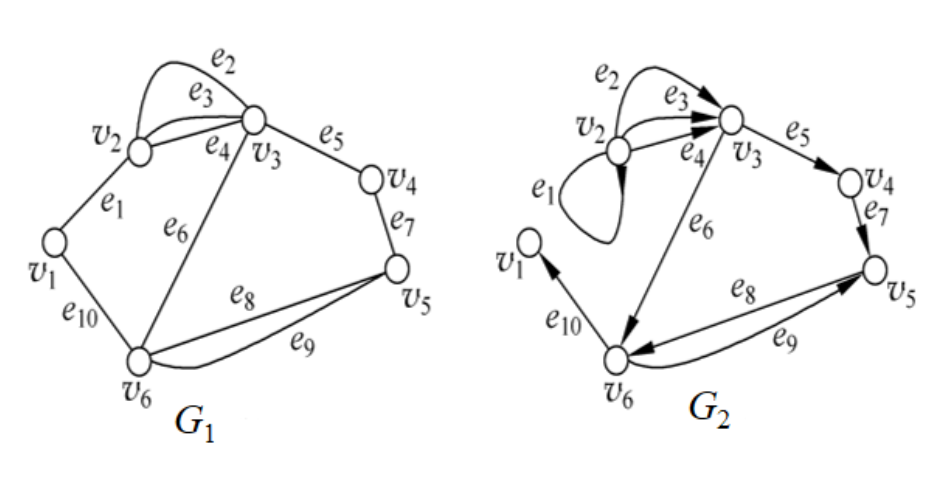
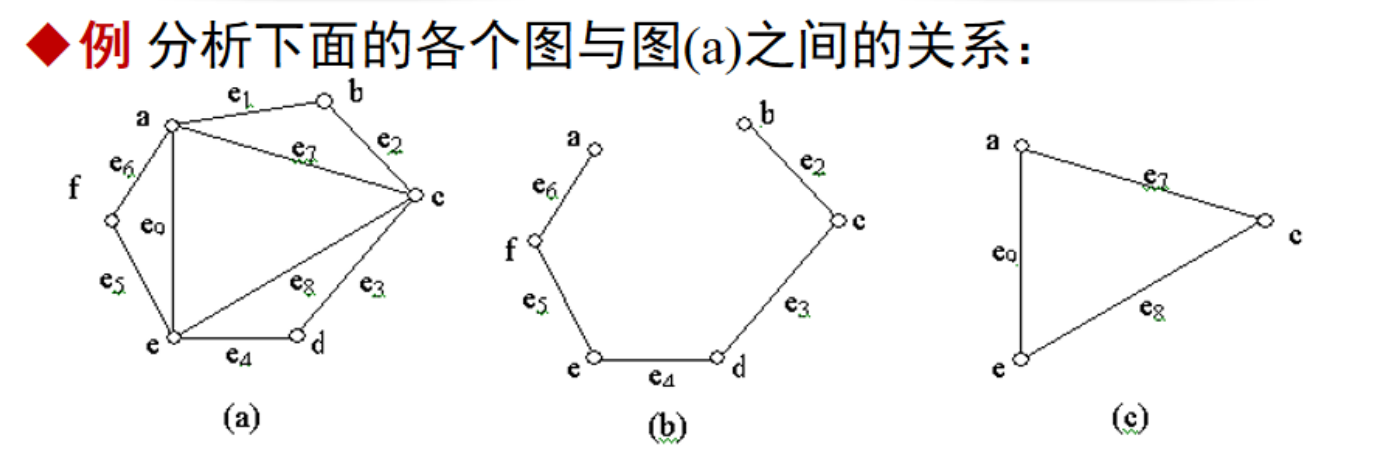
G1为无向图,G2为有向图。
G1中,e2、e3、e4就是平行边
G2中,e2、e3、e4也是平行边,而且e1是自环。
图的分类
多重图:含有平行边的图。
简单图:既不含平行边,又不含有自环的图。
无向图:所有边都是无向边的图。
无向简单图:简单图+无向图。
有向图:所有边都是有向边的图。
有向简单图:简单图+有向图。
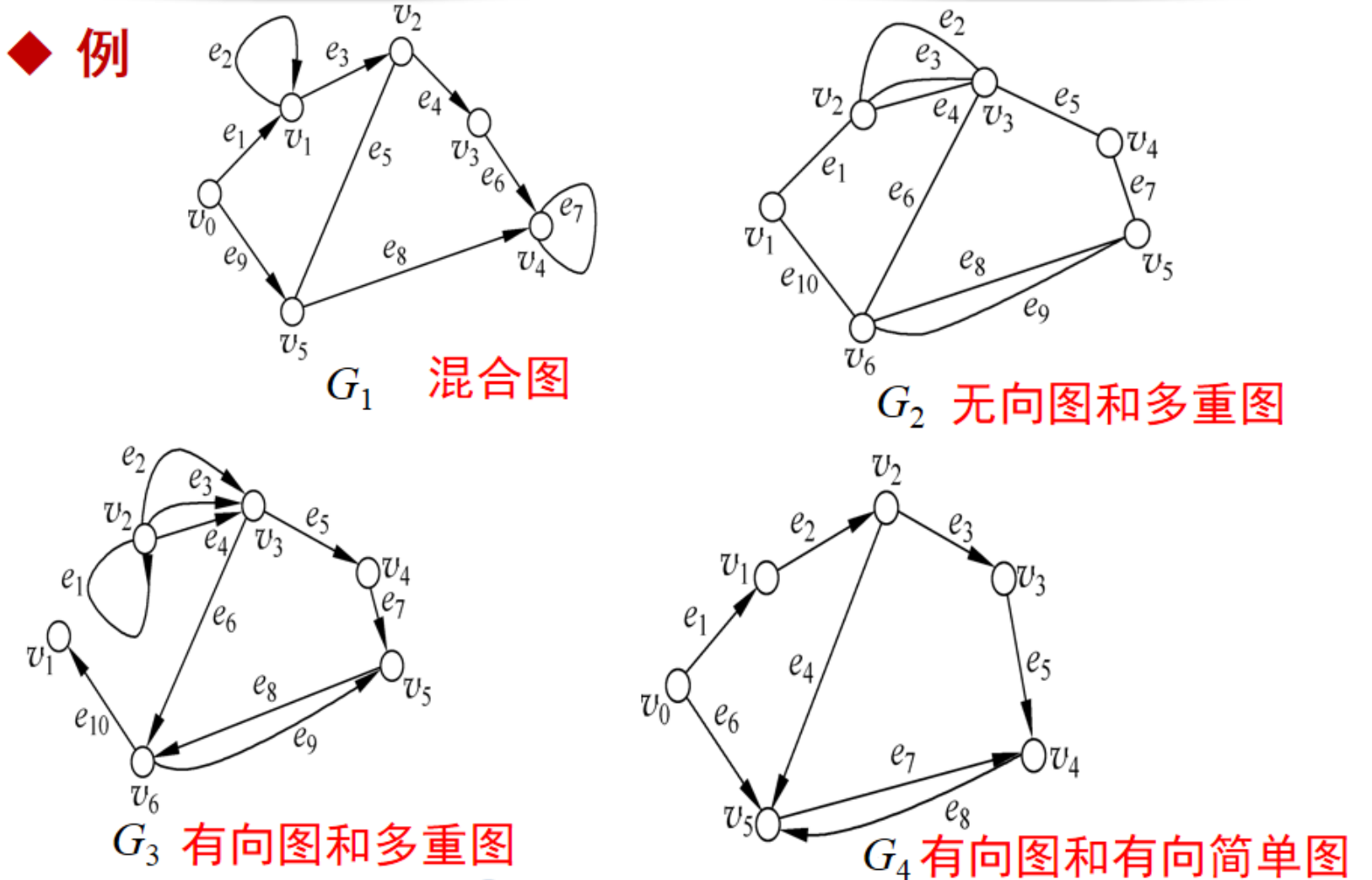
混合图:既含有有向边,又含有无向边的图。
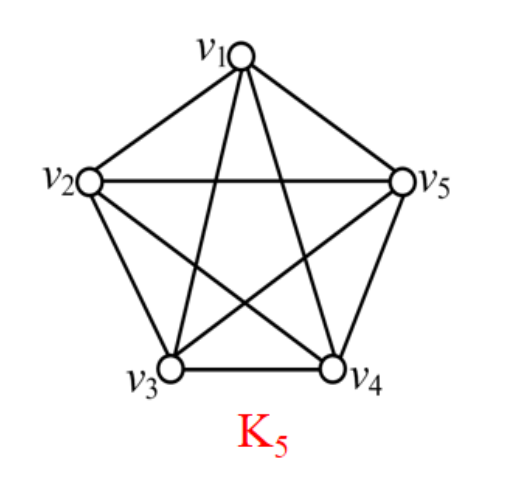
无向完全图(完全图):对于具有n个结点的无向简单图G = <V, E>,如果任意两个结点之间都有边相连,则称G为无向完全图,简称为完全图,记为Kn。
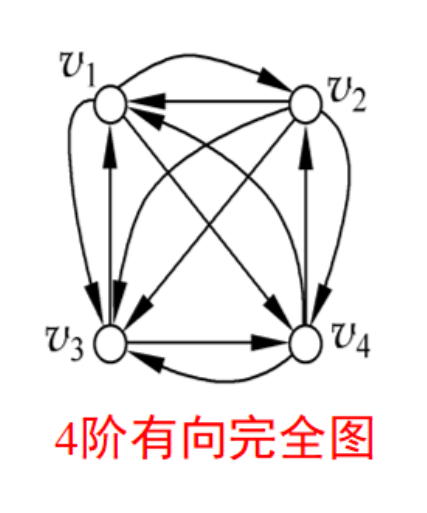
有向完全图:对于具有n个结点的无向简单图G = <V, E>,如果任意两个结点之间都有两条方向相反的有向边相连,则称G为有向完全图。
子图
设G = <V, E>、G1 = <V1, E1>是两个图(同为无向图或同为有向图)。
子图:若V1 V 并且 E1
E,则称图G1是图G的子图,G是G1的母图,记作G1
G。
真子图:若G1 G并且G1 ≠ G,则称G1是G的真子图,记作G1
G。
生成子图:若G1 G 并且 V1 = V(即顶点不减少),则称G1是G的生成子图。
导出子图:若 ,以
为结点集、两个端点都在
中的边的全体为边集的G的子图,称为结点集
导出的导出子图,记作
;若
,以
为边集、
中边的端点全体为结点集的G的子图,称为边集
导出的导出子图,记作
。

结点度数
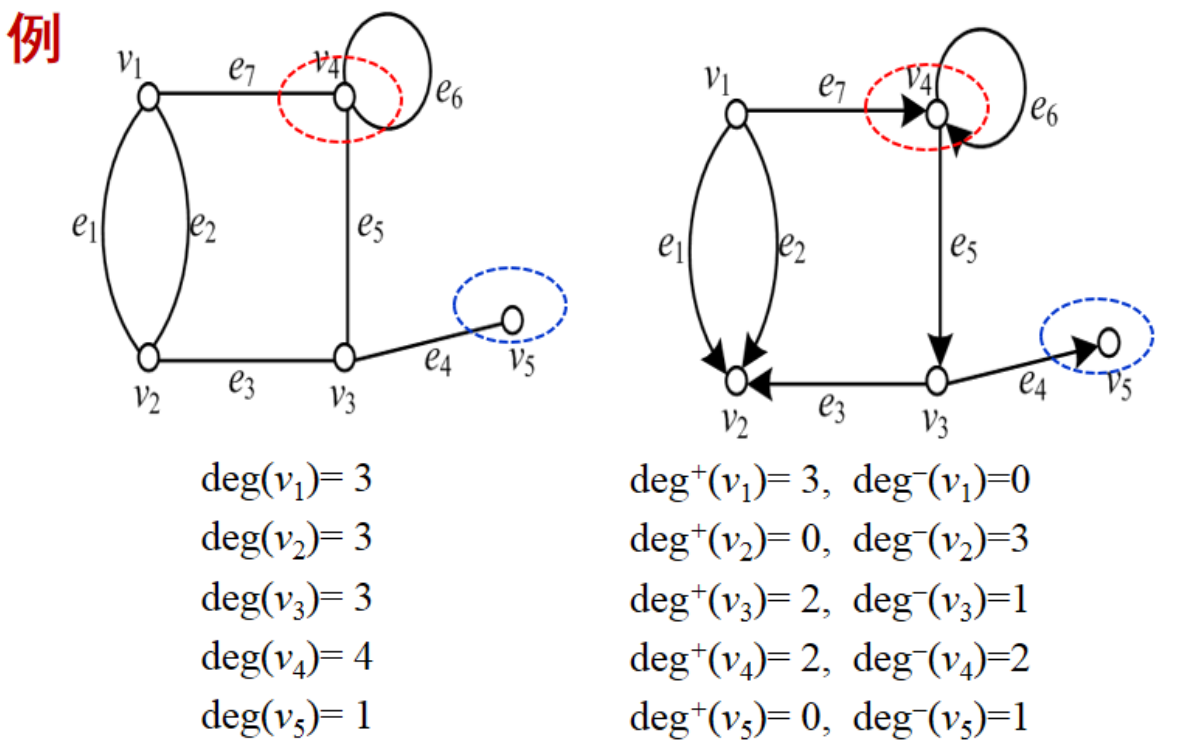
度:在图G = <V, E>中,以结点v∈V为端点的次数称为结点v的度数,简称度,记为 ;
出度:在有向图G = <V, E>中,以结点v∈V为始点的边的数目称为结点v的出度,记为 ;
入度:在有向图G = <V, E>中,以结点v∈V为终点的边的数目称为结点v的入度,记为 。
度 = 出度 + 入度:
入度 = 出度 = 边数:
握手定理:设G = <V, E>中,结点度数的总和等于边的数目的2倍,即 (推论:任意图中度数为奇数的结点个数为偶数)
注意:一个自环能增加两个度。
同构
同构的定义看起来真的又臭又长,比较难理解,我这边直接用大白话了。
图的同构是指两个图在结构上完全相同,只是顶点的名称或位置不同。可以想象成两个图形可以通过重新标记顶点或调整边的位置变得一模一样。
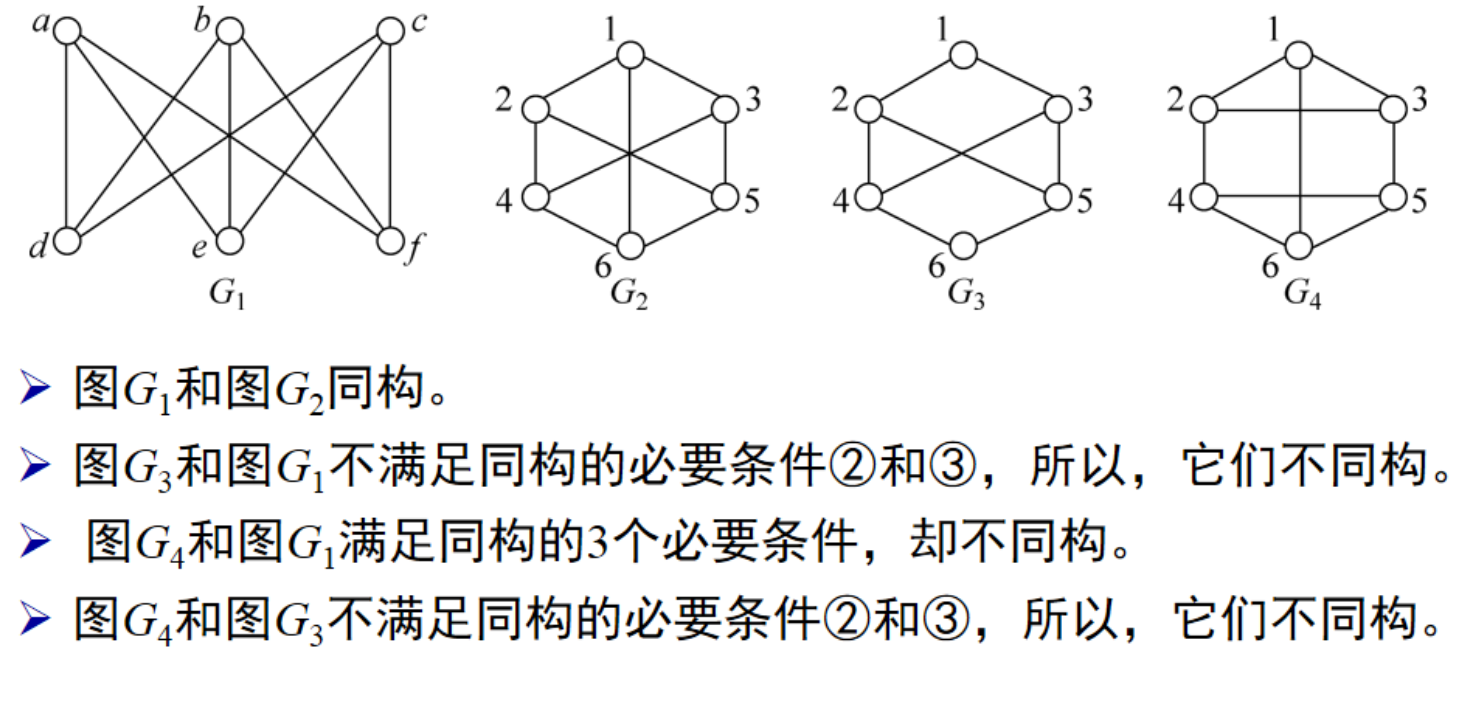
同构的必要条件:
1)节点数目相同;
2)边数相同;
3)度数相同的结点数目相同。
图的连通性
通路:在(无向)有向图G = <V, E>中,结点和边的交替序列称为结点
到
的通路,简记为
。
长度:一条通路中所含有的边的总数。
简单通路:不含有相同边的通路。
基本通路(初级通路):不含有相同结点的通路。
回路:在(无向)有向图G = <V, E>中,结点u到v的通路满足u = v,则称该通路为经过结点u的回路。
简单回路:不含有相同边的回路称为简单回路。
基本回路(初级回路):除结点u和v(u=v)外,不含有相同结点的回路。
无向图
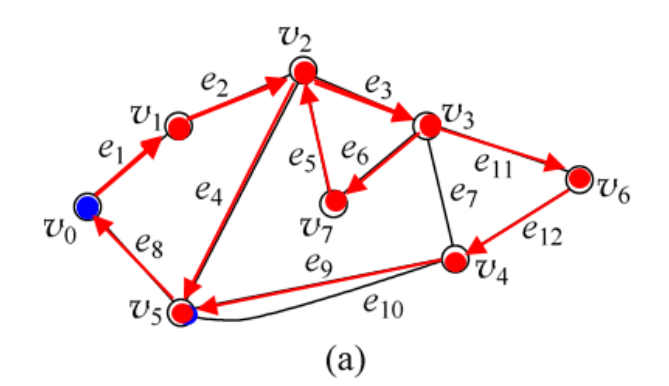

有向图
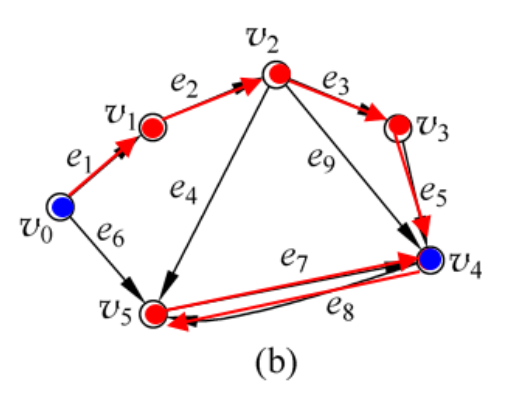

可达(连通):在图G = <V, E>中,如果存在结点u到结点v的通路,则称结点u到结点v是可达的,或是连通的。(规定u到自身总是可达的)
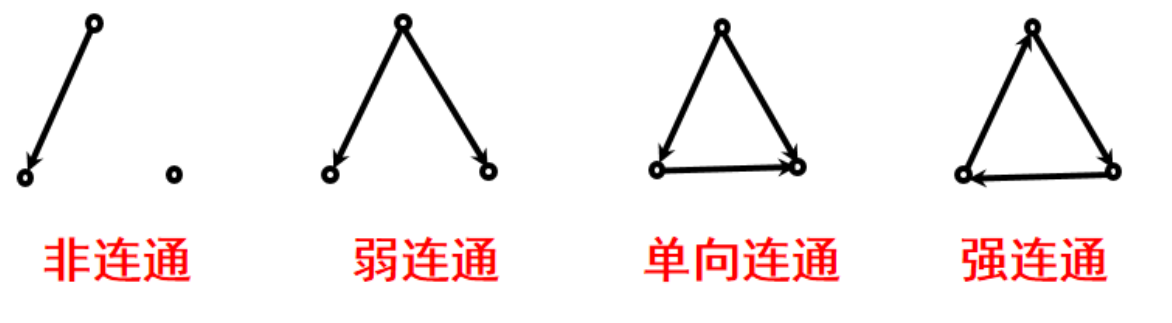
连通图:在无向图G = <V, E>中,如果任何两个结点都是连通的。
弱连通图(连通图):在有向图G = <V, E>中,若略去有向边的方向所得到的无向图是连通图。
单向连通图:在有向图G = <V, E>中,任意两个结点u∈V和v∈V,都有从u到v或从v到u的通路。
强连通图:在有向图G = <V, E>中,任意两个结点u∈V和v∈V,都有从u到v和从v到u的通路。
强连通图 单向连通图
弱连通图
最短路径
赋权图
对图G = <V, E>,其中V = {v1, v2, ... ,vn},E = {e1, e2, ... , en}。
对任意边 e = (vi, vj) 或 e = <vi, vj>标注一个属性 w(vi, vj),所得的图称为赋权图或带权图,记为G = <V, E, W>。
w(e)称为边e的权,或者边e的长度,简记为W(vi, vj)或Wij。
说白话就是边有数值。
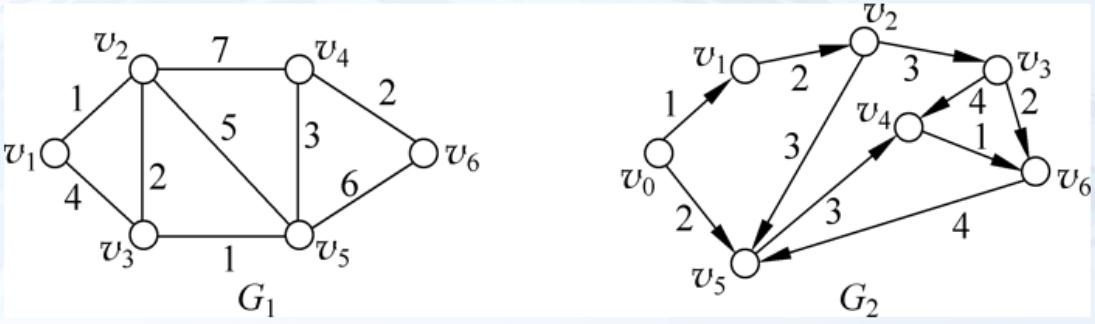
下面是G1、G2的边权矩阵,就是把原来点上的值改为权值。

Dijkstra算法
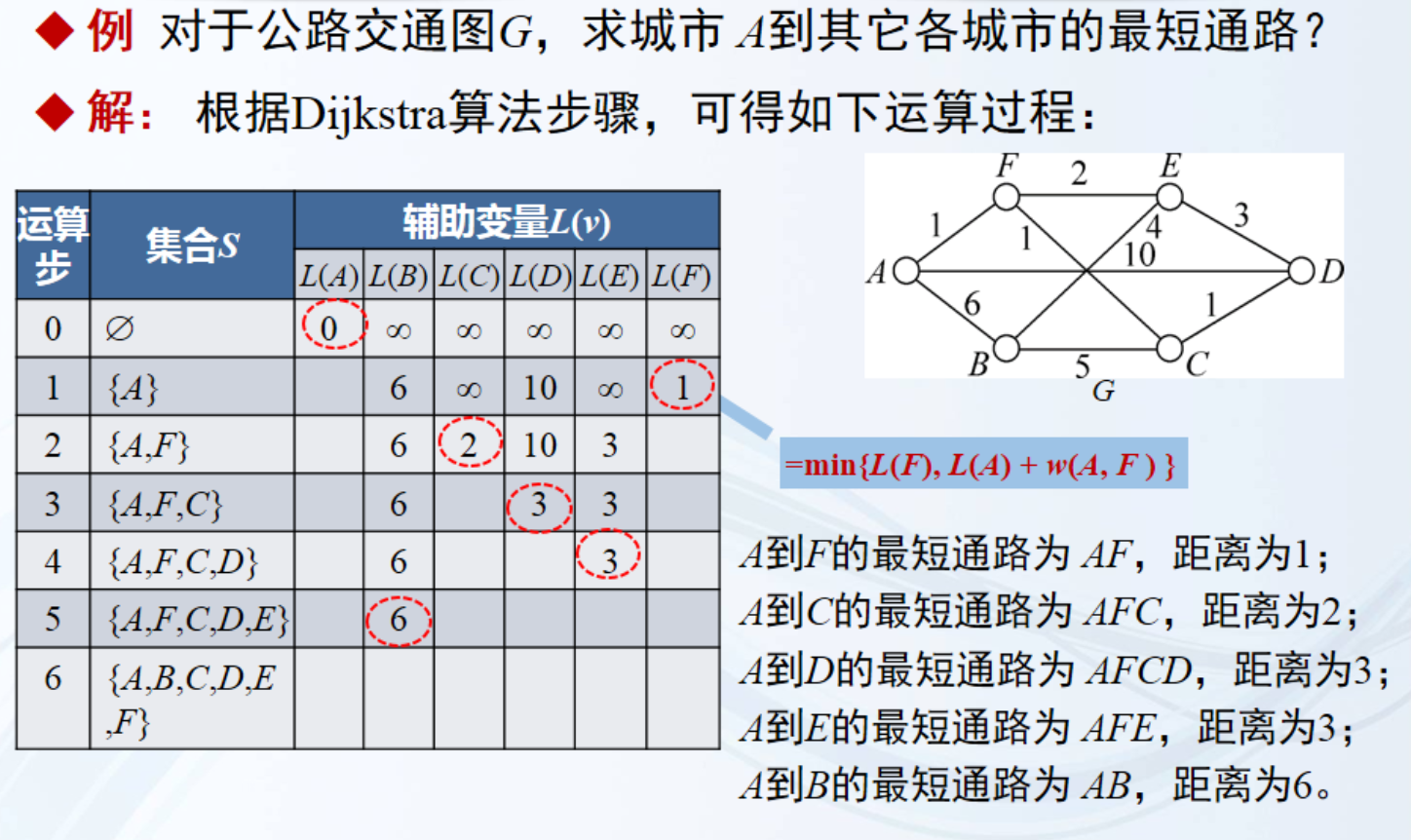
在赋权图中,从某个指定结点出发,求到达任意其它结点的最短通路。

这个算法步骤看起来又臭又长,我说白了就是每次找距离起点最短距离的结点,然后再用这个找到的结点去更新剩余没有被访问的结点。
大家如果不是很理解的话可以去看下面这个up主讲的,很详细容易懂。
图-最短路径-Dijkstra(迪杰斯特拉)算法_哔哩哔哩_bilibili
欧拉图
欧拉图说白话就是能一笔画的图。
欧拉通路:经过G中每条边一次且仅一次的通路。
欧拉回路:经过G中每条边一次且仅一次的回路。
欧拉图:具有欧拉回路的图。
半欧拉图:具有欧拉通路但不具有欧拉回路的图。
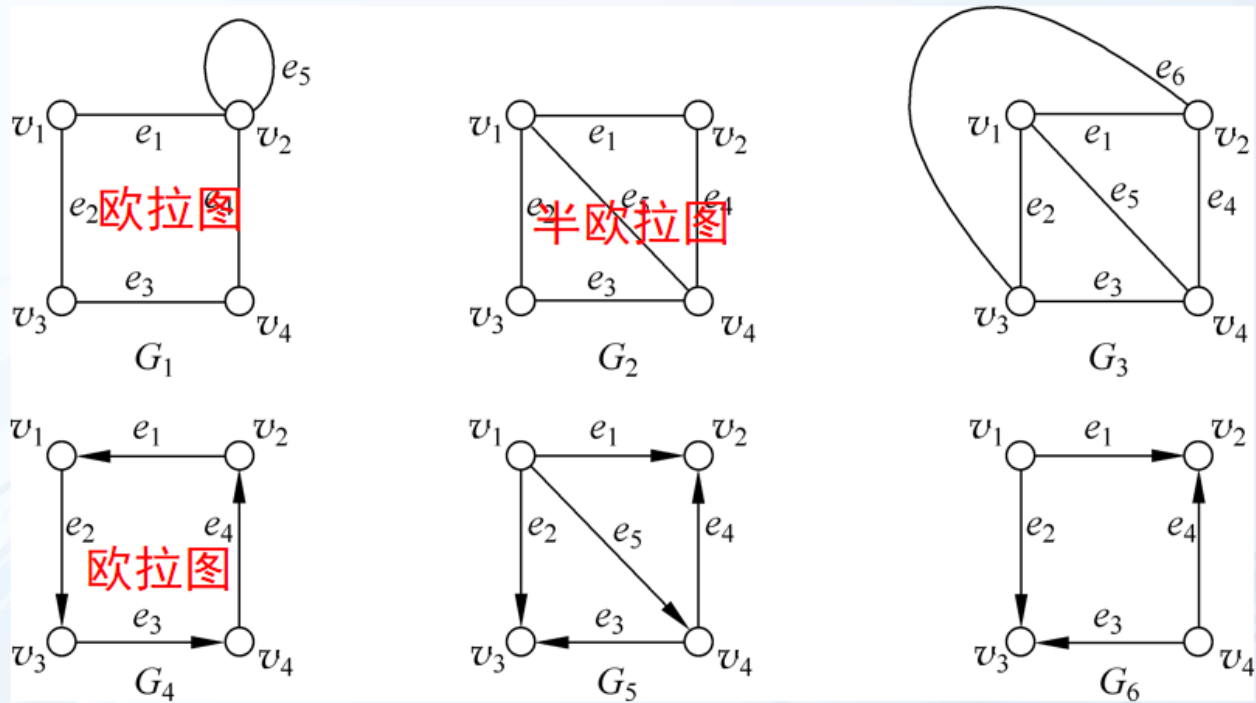
对于任一无向图G,当且仅当G是连通的,且有零个或两个奇度数结点时,
1)若无奇度结点,则欧拉通路为欧拉回路;
2)若有两个奇度结点,则它们是每条欧拉通路的端点。
对于有向图G = <V, E>,当且仅当G是连通的,
1)所有结点的入度等于出度,为欧拉回路。
2)除了两个结点以外,其余结点的入度和出度相等,而这两个例外的结点中的一个结点的入度比出度大1,另一个结点的入度比出度小1。
哈密顿图
哈密顿通路:G中经过每一个结点一次且仅一次的通路。
哈密顿回路:G中经过每一个结点一次且仅一次的回路。
哈密顿图:具有哈密顿回路的图。
半哈密顿图:具有哈密顿通路但不具有哈密顿回路的图。
哈密顿图的充分条件(符合条件的是哈密顿图,但不符合的不一定不是哈密顿)
1)哈密顿通路:任意两个不相邻结点度数之和都大于等于n-1。
2)哈密顿回路:任意两个不相邻结点的度数之和都大于等于n(或任意结点都有deg(v) ≥ n/2)。
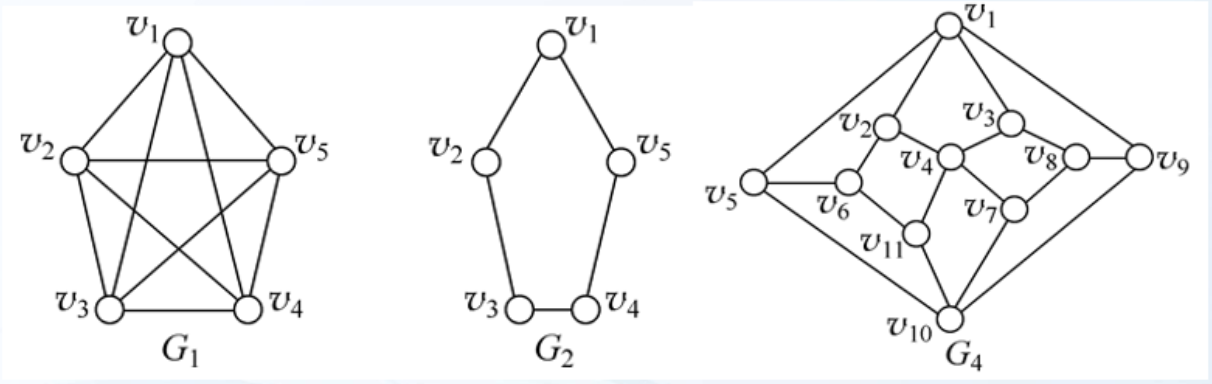

判断哈密顿图,实际上也就是一笔画,看能不能经过所有的结点,如果比较难判断时,大家可以直接举出回路或通路来说明是不是哈密顿图。
树的概念
无向树
无向树:连通且不含有回路的无向图。
森林:每个连通分支都是树的无向图。
叶:度数为1的结点。
内部结点(分支结点):度数大于1的结点。
如果T = <V, E>是树,则 |E| = |V| - 1。
非同构树
不同的度数方案对应的树是不同构的。
6个结点(|E| = |V| - 1 = 5)的非同构树:

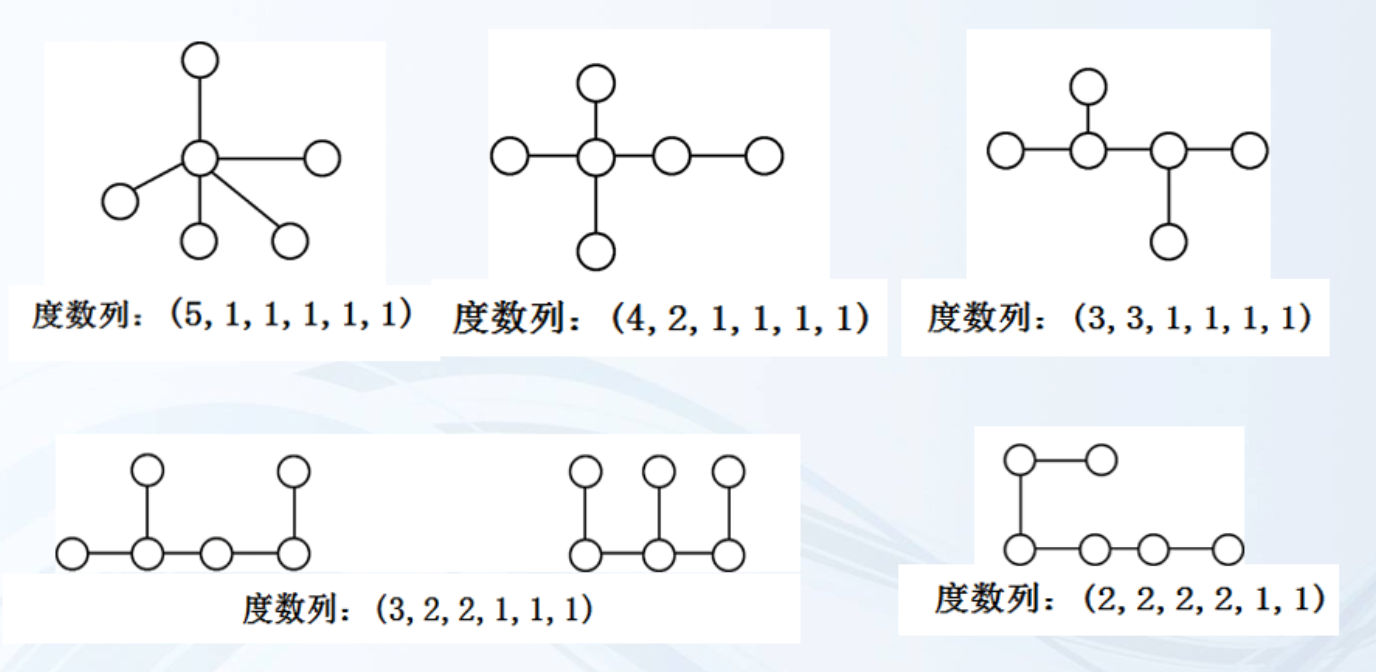
有向树
有向树:若略去有向图G中所有有向边的方向所得到的无向图是一棵树,则称G是有向树。
根:入度为0的结点。
叶:入度为1出度为0的结点。
内部结点(分支结点):除叶和根以外的其余结点。
如果T = <V, E>是树,则 |E| = |V| - 1。
根树(数据结构中一般指的就是根树)
根树:有向树T中,只有1个结点的入度为0,其余结点的入度均为1。
树根:根结点。
树叶:叶结点。
层数:从树根到任意结点v的通路的长度。
树高:结点的最大层数。
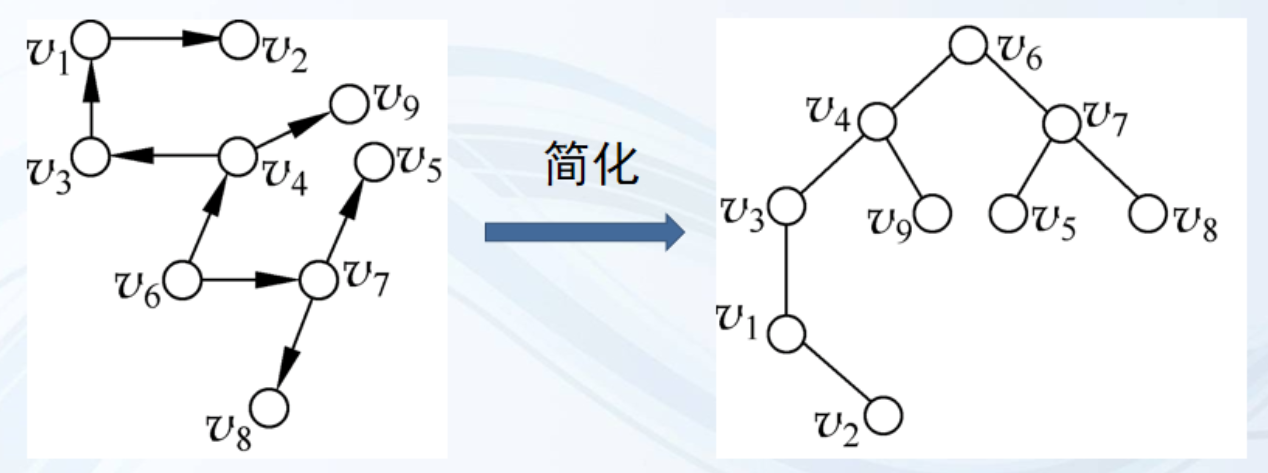
根树的化简:
将树根放在最上面,然后按照结点的层数,逐渐向下递增,略去有向边的箭头,对其进行重画。
最小生成树
生成树:对于无向连通图G = <V, E>,如果 T = <V, E*>是G的生成子图,且T为树,则称T是G的生成树。
最小生成树:权值最小的赋权(就是边有权值)生成树。
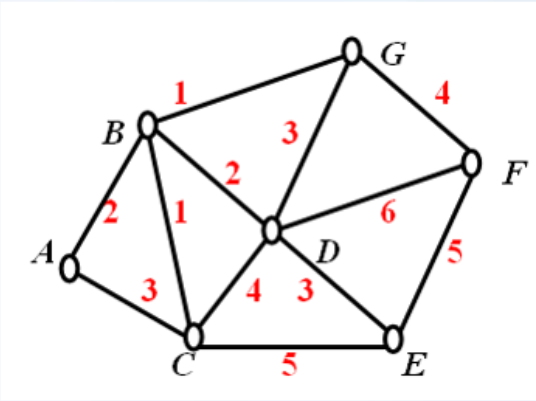
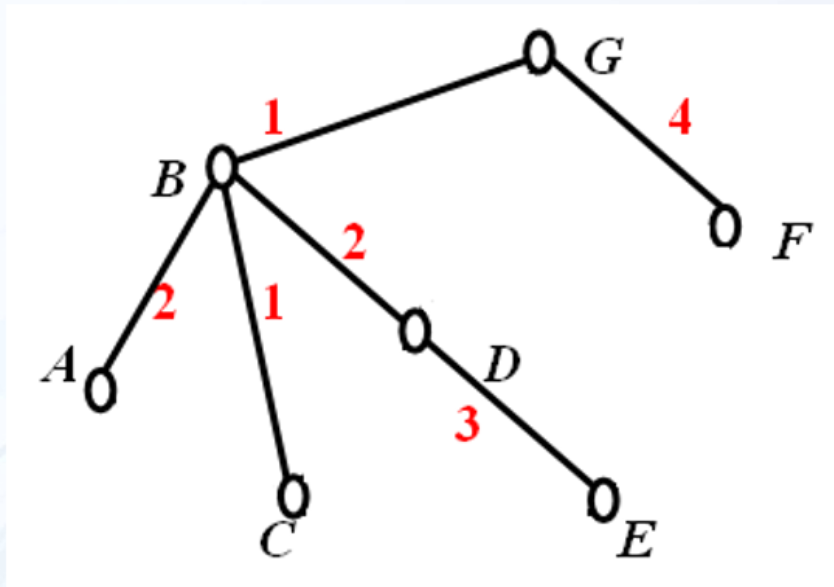
kruskal算法
对每条边按权值排序,每次选取最小的那条边,如果属于同一并查集(已经存在通路),则跳过,直到构成生成树(选够|V|-1条边),这个生成树就是最小生成树。
最优树
二叉树:每个分支结点至多有2个儿子。
1)满足层数 l(v) = i 的结点数目至多 个;
2)高度 h(T) = k 的二叉树的结点数目至多 个;
3)如果叶结点的个数为n1,出度为2的结点个数为n2,则n1 = n2 + 1。
前缀码
1)在一个二叉正则树(每个分支结点恰好有2个儿子),将每个结点和它的左儿子之间的边标记为0,和它右儿子之间的边标记为1;
2)将树根到每个树叶的通路所经过的边的标记序列作为树叶的标记。
树叶的标记就是前缀码。
最优二叉树(哈夫曼树)
权值最小的二叉树,使用Huffman算法构造。
一般权值是指出现的频率、出现的概率。
左儿子 < 右儿子(权值)
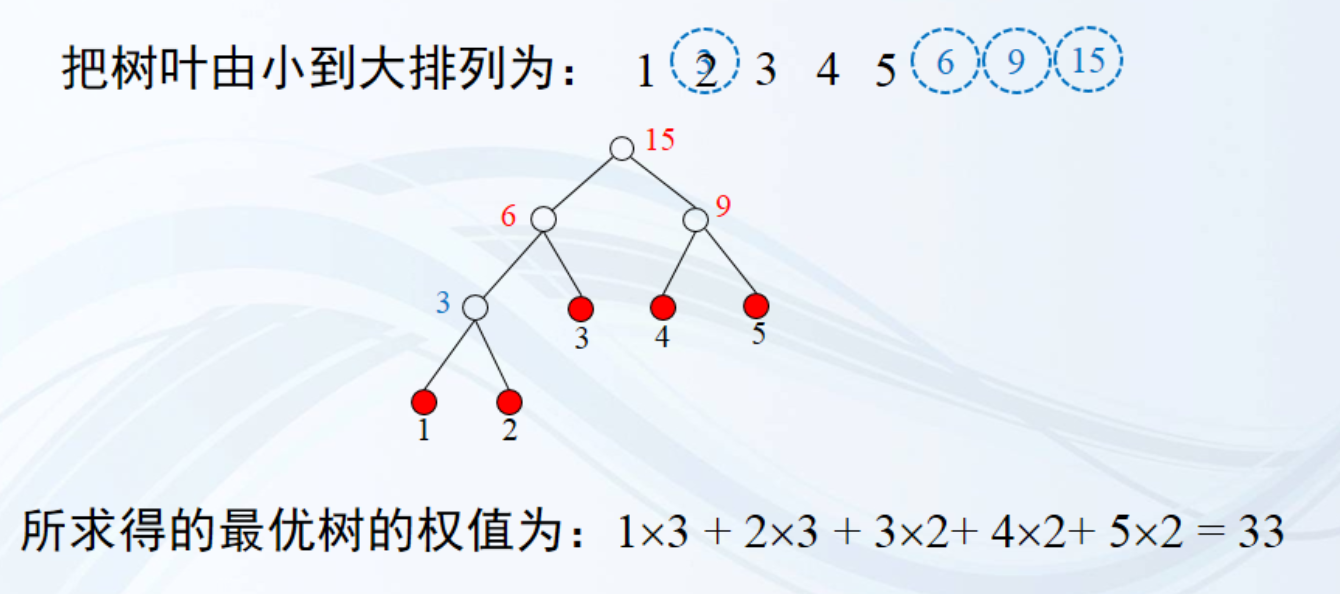
简单来说就是,每次从数组中选择最小权值的两个结点,把它们构造成左小右大的二叉树,构造成的二叉树作为新的结点(权值为两个结点权值的和)放回数组中,直到剩下一个结点,就是最优树。

例:求树叶赋权为4、2、3、5、1的最优树。
ps:博主已经被榨干,大家点点赞,没点关注的点点关注。





















 2097
2097

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








