一些概念
集成电路分类
①模拟集成电路,处理连续信号
②数字集成电路,处理离散信号
数字集成电路分类
逻辑集成电路 储存器 ASIC(Application Specific IC)
特点
信号表示形式统一、便于计算机处理
可靠性高
工艺成熟、可大规模集成
集成度
SSI 1-10门,逻辑门电路
MSI 10-100门,计数器、移位寄存器
LSI 1000-1000门 小型储存器,八位算术逻辑单元
VLSI 1000-1w门 大型储存器、微处理器
ULSI 超过100w门 编程逻辑器件、多功能集成电路
摩尔定律
集成度18月翻一番
后续相关课程
计算机组成和实践 嵌入式系统 DSP
CPU内部结构
ALU
寄存器 (通用寄存、地址寄存,状态寄存
译码器(指令
计数器(程序
时序发生器
内存
课程内容
数字逻辑基本理论:逻辑代数
无记忆逻辑电路:组合逻辑电路
有记忆逻辑电器:触发器、时序逻辑电路(同步、异步
可编程逻辑器FPGA和硬件描述语言verilog HDL
1.1 逻辑代数概述
二值逻辑:条件、结论只取对立两值,是非、对错、真假
逻辑代数中,1代表真,0代表假
1与0是逻辑概念,只代表真假、无大小
数字逻辑中1和0表示二进制数,仅为一种代码,实际运算还是靠逻辑运行
逻辑函数
用一个数学表达式描述逻辑关系问题
Y=f(A,B)Y = f(A,B)Y=f(A,B)
表示方法
真值表
逻辑函数
逻辑图
卡诺图
硬件描述语言(HDL
逻辑运算
与
Y=A⋅BY = A\cdot BY=A⋅B
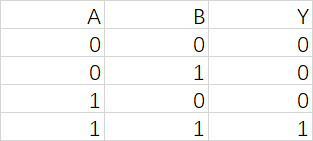
或
Y=A+BY = A+ BY=A+B
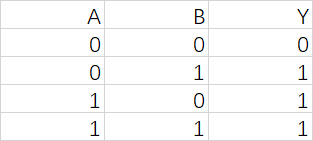
非
Y=A‾Y = \overline{A}Y=A
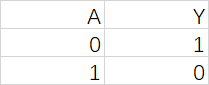
反函数
逻辑函数互为反函数,对输入变量任意取值,输出逻辑值相反

F和G互为反函数
复合逻辑运算
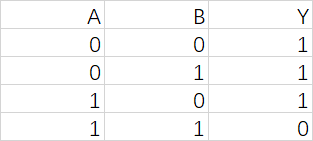
与非
先对AB进行与运算再进行非运算
Y=A⋅B‾Y = \overline{A\cdot B}Y=A⋅B
或非
先对AB进行或运算再进行非运算
Y=A+B‾Y = \overline{A+ B}Y=A+B
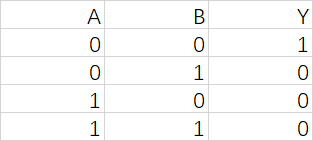
异或
Y=A⊕BY=AxorBY=A\oplus B\quad Y = A xor BY=A⊕BY=AxorB
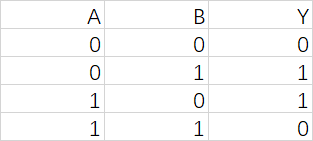
同或Y=A⊙BY = A \odot BY=A⊙B
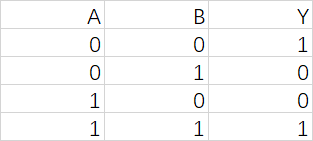
逻辑图:基本逻辑单元
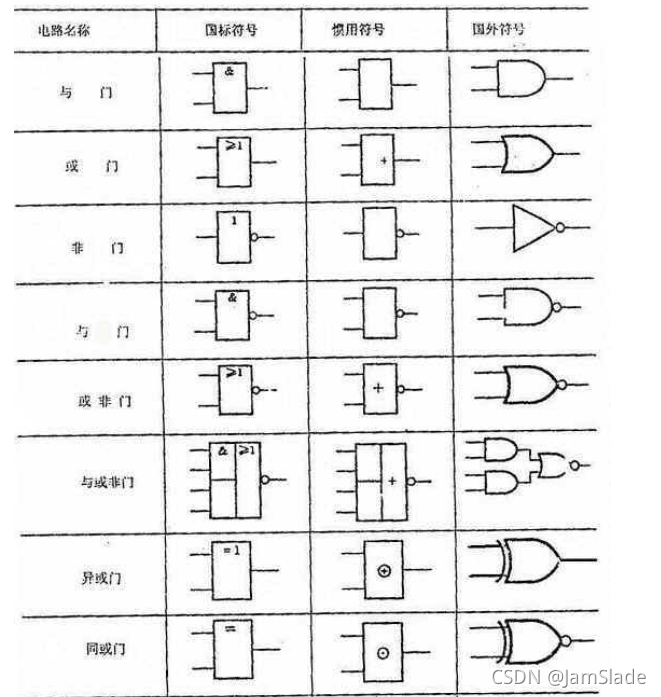
逻辑图符号标准规定
所有逻辑符号由方框、标注在方框内总限定符号组成
组合形式逻辑图
利用国标图形可以讲线路省去,直接拼凑
1.2逻辑代数基本定理
一、零一律
A⋅1=AA+0=AA⋅0=0A+1=1A\cdot1=A\qquad A+0=A\\ A\cdot0=0\qquad A+1=1A⋅1=AA+0=AA⋅0=0A+1=1
二、等幂律
A⋅A=AA+A=AA\cdot A = A\qquad A+A = AA⋅A=AA+A=A
三、互补律
A⋅A‾=0A+A‾=1A\cdot \overline{A }= 0\qquad A+\overline{A } =1A⋅A=0A+A=1
四、自反律
A‾‾=A\overline{\overline{A}} =AA=A
五、交换律
AB=BAA+B=B+AAB=BA \qquad A+B = B + AAB=BAA+B=B+A
六、结合律
A(BC)=(AB)CA+(B+C)=(A+B)+CA(BC)=(AB)C\\ A+(B+C)=(A+B)+CA(BC)=(AB)CA+(B+C)=(A+B)+C
七、分配律
A(B+C)=AB+ACA+BC=(A+B)(A+C)A(B+C)=AB+AC \\A+BC = (A+B)(A+C)A(B+C)=AB+ACA+BC=(A+B)(A+C)
八、反演律
AB‾=A‾+B‾A+B‾=A‾⋅B‾\overline{AB} = \overline{A}+\overline{B} \qquad \overline{A+B} = \overline{A}\cdot\overline{B}AB=A+BA+B=A⋅B
九、代入定理
任何逻辑等式中,其中一个逻辑变量全部用另一个逻辑函数代替
十、反演定律
对一个逻辑函数式子:
①所有逻辑符号·和+交换
②所有逻辑常量 1 0 互换
③所有逻辑变量取反
④不改变运算顺序
得到逻辑函数是原来的反函数(例子:德摩根定理
Y=A(B‾+C)+CDY‾=(A‾+BC‾)(C‾+D‾)Y = A(\overline{B}+C)+CD\\ \overline{Y}=(\overline{A}+B\overline{C})(\overline{C}+\overline{D})Y=A(B+C)+CDY=(A+BC)(C+D)
十一、对偶关系
逻辑符号+和·
逻辑常量1和0
①所有逻辑符号+和·互换
②逻辑常量1和0互换
若两个函数相等,他们的对偶式形成的两个函数也相等
若(A+D)C‾=AC‾+C‾D+0则AD+C‾=(A+C‾)(C‾+D)⋅1若\qquad(A+D)\overline{C}=A\overline{C}+\overline{C}D+0\\ 则\qquad AD+\overline{C}=(A+\overline{C})(\overline{C}+D)\cdot1若(A+D)C=AC+CD+0则AD+C=(A+C)(C+D)⋅1
常用逻辑恒等式
一、吸收率
①A+AB=A②A(A+B)=A③A+A‾B=A+B④A(A‾+B)=AB⑤A⋅AB‾=AB‾⑥A+A+B‾=A+B‾⑦AB+A‾B=B⑧(A+B)(A‾+B)=B①\quad A+AB = A\\②\quad A(A+B)=A\\ ③\quad A+\overline{A}B = A+B\\④\quad
A(\overline{A}+B)=AB\\⑤\quad A\cdot \overline{AB} = A\overline{B}\\ ⑥ \quad A+\overline{A+B} = A+\overline{B}\\⑦\quad AB+\overline{A}B = B\\⑧\quad (A+B)(\overline{A}+B)=B
①A+AB=A②A(A+B)=A③A+AB=A+B④A(A+B)=AB⑤A⋅AB=AB⑥A+A+B=A+B⑦AB+AB=B⑧(A+B)(A+B)=B
二、冗余律
①AB+A‾C+BC=AB+A‾C②(A+B)(A‾+C)(B+C)=(A+B)(A‾+C)③AB+A‾C+BCD=AB+A‾C④(A+B)(A‾+C)(B+C+D)=(A+B)(A‾+C)①\quad AB+\overline{A}C +BC = AB+\overline{A}C \\②\quad (A+B)(\overline{A}+C)(B+C)=(A+B)(\overline{A} + C)\\ ③\quad AB+\overline{A}C+ BCD = AB+\overline{A}C\\④\quad (A+B)(\overline{A}+C)(B+C+D)=(A+B)(\overline{A}+C)
①AB+AC+BC=AB+AC②(A+B)(A+C)(B+C)=(A+B)(A+C)③AB+AC+BCD=AB+AC④(A+B)(A+C)(B+C+D)=(A+B)(A+C)
1.3逻辑函数的化简和形式转换
异或的不同表达形式:
与或形识
A‾B+AB‾\overline{A}B+A\overline{B}AB+AB
与非—与非形式
A‾B‾⋅AB‾‾‾\overline {\overline{\overline{A}B} \cdot \overline{A\overline{B}}}AB⋅AB
与或 和 与非—与非形式可以相互转换
或与形式
(A‾+B‾)(A+B)(\overline{A}+\overline{B})(A+B)(A+B)(A+B)
或非—或非形式
A‾+B‾‾+A+B‾‾\overline{ \overline{\overline{A}+\overline{B}} +\overline{A+B} }A+B+A+B
与或非形式
AB+A‾⋅B‾‾\overline{AB+\overline{A}\cdot\overline{B}}AB+A⋅B
混合形式
AB‾(A+B)\overline{AB}(A+B)AB(A+B)
后四种情况相互转换
目标函数要求:
逻辑电路数量少(面积约束
逻辑电路级数最少(速度约束
输入端数量最少(混合约束
电路为拟定(避免竞争、冒险





 本文介绍了数字集成电路的基本类型和分类,包括模拟集成电路和数字集成电路,重点讲述了数字集成电路中的逻辑门电路、存储器及其集成度级别。同时,深入探讨了逻辑代数的基本原理,如逻辑运算、逻辑函数表示、逻辑恒等式和化简方法。内容涵盖了摩尔定律、组合逻辑电路、时序逻辑电路以及可编程逻辑器件FPGA和硬件描述语言Verilog HDL的基础知识。
本文介绍了数字集成电路的基本类型和分类,包括模拟集成电路和数字集成电路,重点讲述了数字集成电路中的逻辑门电路、存储器及其集成度级别。同时,深入探讨了逻辑代数的基本原理,如逻辑运算、逻辑函数表示、逻辑恒等式和化简方法。内容涵盖了摩尔定律、组合逻辑电路、时序逻辑电路以及可编程逻辑器件FPGA和硬件描述语言Verilog HDL的基础知识。

















 9830
9830

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








