目录
命题符号化
命题
自然语言中能够判断真假的陈述句。
常值命题:一个特定的命题,不是具有值 "T(1)" 就是具有值 "F(0)"。
简单命题(原子命题):能够判断真假的简单陈述句,一般用小写或大写英文字母表示一个简单命题(如,p、q、P、Q...等)。当简单命题不是一个常值时,又称为命题变元。
比如:我爸是李刚。
复合命题:通过关联词将简单命题复合连接而成的命题,当简单命题是命题变元时,复合命题又称为命题公式。
比如:我爸是李刚并且且我妈是李乃乃。
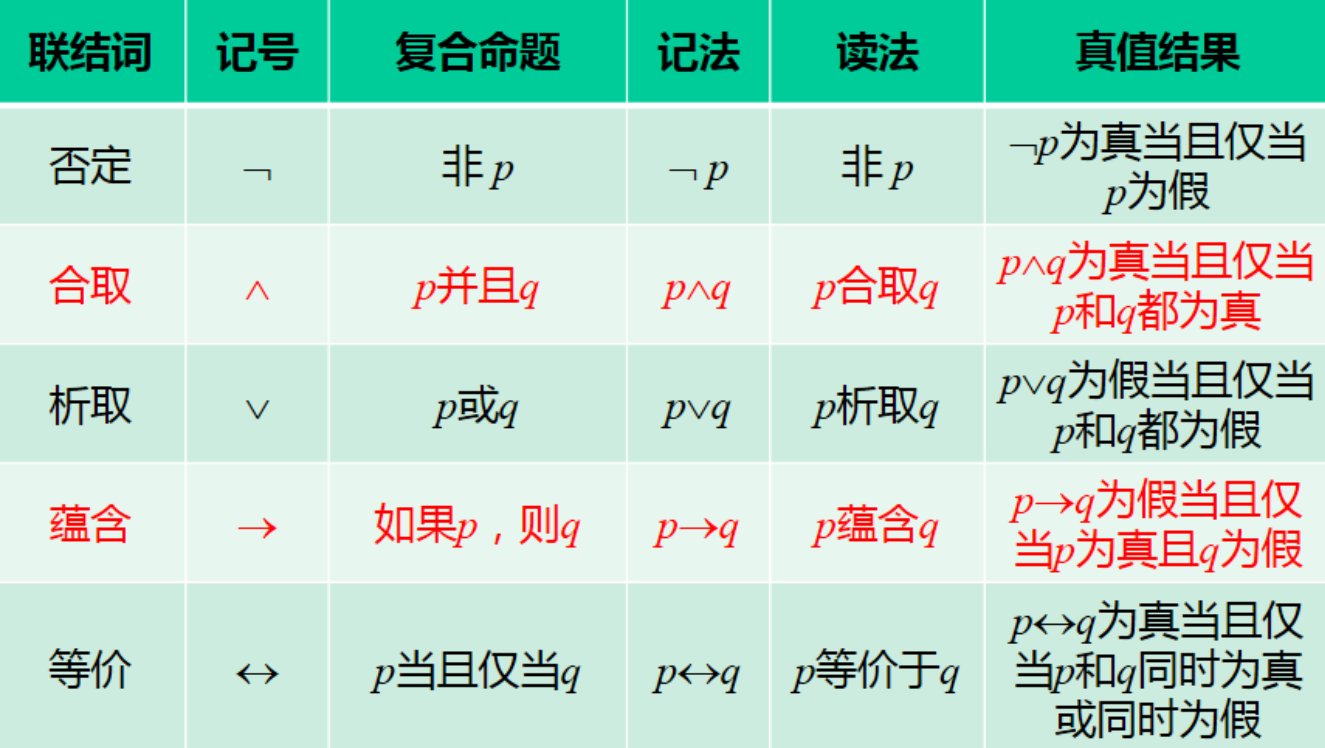
联结词
否定联结词 "┐":设p为任一命题,复合命题 "非p"(或 "p的否定")称为p的否定式,记为┐p。并规定,┐p为真当且仅当p为假。(自然语言中 "非"、"不" 和 "没有" 等关系词的逻辑抽象)
合取联结词 "∧":设p、q为两任意命题,复合命题 "p并且q"(或 "p和q")称为p和q的合取式,记为p∧q。并规定,p∧q为真当且仅当p和q都为真。(自然语言中 "并且"、"和"、"与" 和 "既...又..."等关联词的逻辑抽象)
析取联结词 "∨":设p、q为两任意命题,复合命题 "p或q" 称为p和q的析取式,记为p∨q。并规定,p∨q为假当且仅当p和q都为假。(自然语言中 "或" 和 "或者" 等关系词的逻辑抽象)
蕴含连结词 "->":设p、q为两任意命题,复合命题 "如果p,则q" 称为p和q的蕴含式,记为p->q。并规定,p -> q为假当且仅当p为真且q为假。q是p的必要条件,p是q的充分条件。(自然语言中 "因为p所以q"、"如果...就..."、"只要p就q"、"只有q才p"、"除非q否则非p"、"除非q才p" 和 "p仅当q"等关系词的逻辑抽象)
等价连结词 "<->":设p、q为两任意命题,复合命题 "p当且仅当q" 称为p和q的等价式,记为p<->q。并规定,p <-> q 当且仅当p和q同时为真或同时为假。(自然语言中 "充分必要条件"、"如果...就...反之亦然" 和 "当且仅当" 等关联词的逻辑抽象)
表格从上到下,连结词依次优先级降低。
大家可以看表格速记。
下面列举几个符号化表示命题的例子:


命题公式的等值演算
命题公式的定义
命题公式是由命题变元(如 p、q、r)和逻辑联结词(如 ¬、∧、∨、→、↔)按一定规则构成的符号串。
而命题的符号化就是把自然语言命题转化为逻辑符号。
命题公式的类型
- 永真命题公式(永真公式或重言式):命题公式A在所有解释下的真值都为真,用1表示。
- 可满足命题公式(可满足公式):至少存在一个解释使命题公式A的真值为真。
- 永假命题公式(永假公式或矛盾式或不可满足公式):命题公式A在所有解释下的真值都为假,用0表示。
判断下列命题公式的类型:

命题公式的等值式
如果命题公式A和B的等价式A <-> B是重言式,则称命题公式A与B是逻辑等值的,或者是命题公式的等值式,简称为等值式,记为 A ⇔ B 或 A = B。(注意:⇔不是逻辑连结词,A ⇔ B是表示 A <-> B 为重言式的一种记法)
下面列出一些基本等值式:


等值演算
在命题逻辑中,由已知的等值式,通过等值式替换,推演出另外一些等值式的过程称为命题逻辑的等值演算,简称等值演算。
等值演算的应用
1.简化公式
消去连结词->、<->
尽量让互为否定的命题(例如p与¬p)成对出现。

2.证明两个公式等值
消去连结词->、<->;从两边进行观察。

如果要证明两个公式不等值,用等值演算难以直接证明,
我们可以采用真值表、观察赋值(先用等值演算化简)。
3.判断公式的类型
矛盾式:A ⇔ 0;重言式:A ⇔ 1。
也就是判断命题公式是否与0或1等值,与0等值的是矛盾式,与1等值的是重言式。
既不与0等值又不与1等值时,可以代值判断是否有成真赋值和成假赋值。

命题公式的主范式
命题公式的范式
简单析取式:有限个命题变元或命题变元的否定的析取构成的命题公式。(p∨q、p∨¬q)
简单合取式:有限个命题变元或命题变元的否定的合取构成的命题公式。(p∧q、p∧¬q)
析取范式:有限个简单合取式的析取得到的命题公式。
合取范式:有限个简单析取式的合取得到的命题公式。
注意:
- 单个简单合取式既是合取范式,又是析取范式;
- 单个简单析取式既是析取范式,又是合取范式;
- 单个命题变元或它的否定既是析取范式,又是合取范式(也是简单析取式和简单合取式)。
范式的求取
任意命题公式都存在与之等值的析取范式和合取范式,而且命题公式的析取范式、合取范式不一定唯一。
求取范式步骤:
- 消去连结词->,<->;
- 将否定连结词¬内移,同时消去双重否定符,使得¬仅出现在命题变项的前面;
- 使用分配律得到相应的范式。

极大极小项
极小项:简单合取式,每个命题变元(q)与其否定(¬q),二者之一仅出现一次(即不是q就是¬q,二者只能有一个)。(比如:p∧q、p∧¬q)
极大项:简单析取式,每个命题变元(q)与其否定(¬q),二者之一仅出现一次(即不是q就是¬q,二者只能有一个)。(比如:p∨q、p∨¬q)
n个命题变元可以生成2^n个极小项和2^n个极大项。
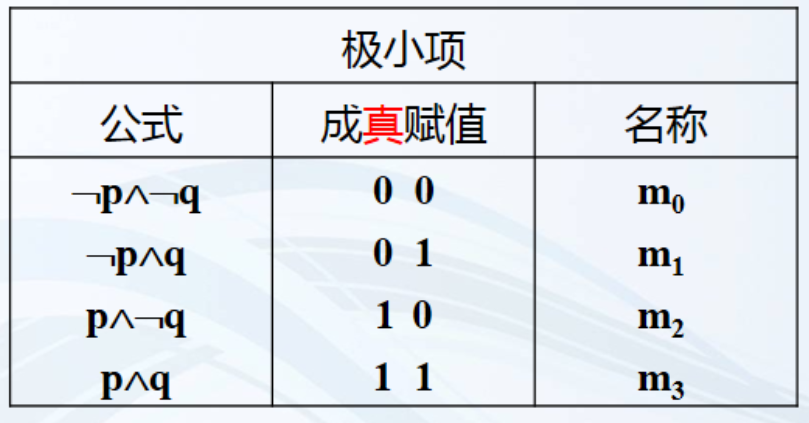
极小项的简写:
对于每个极小项,把它的成真赋值看作二进制数,令相应的十进制数为i,则用mi来指代这个极小项。
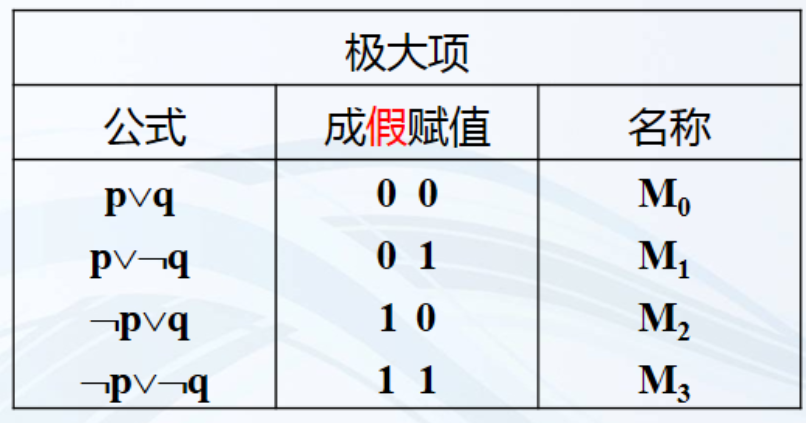
极大项的简写:
对于每个极大项,把它的成假赋值看作二进制数,令相应的十进制数为i,则用Mi来指代这个极大项。
命题公式的主范式
主析取范式:析取范式,其中的每一个简单合取式都是该n个命题变元的极小项。
主合取范式:合取范式,其中的每一个简单析取式都是该n个命题变元的极大项。
任何命题公式都存在与之等值的主析取范式和主合取范式,并且是唯一的,可以用来判断两个命题是否等值。
例举:

主范式之间的转换
对于任何一个含有n个命题变元的命题公式A:
如果A的主析取范式为mi1 V mi2 V ... V mik
其中没有出现的极小项为mj1, mj2, ... , mjr (r+k = 2^n)
则A的主合取范式为Mj1 ∧ Mj2 ∧ ... ∧ Mjr
就比如:
对于3个命题变元的命题公式A,
主析取范式:m0 ∨ m1 ∨ m3 ∨ m5 ∨ m7
主合取范式:M2 ∧ M4 ∧ M6
命题逻辑推理的构造证明法
命题逻辑推理
对于命题公式A和B,如果蕴含式 A -> B 的所有赋值都是成真赋值,那么,称该蕴含式为永真蕴含式或重言蕴含式,记为 A ⇒ B(注意:⇒不是逻辑连结词,只是A -> B永真时的一种简单记法。)。
简单证明推理
命题逻辑推理的两种转换:
1.直接方法:证明 A1 ∧ A2 ∧ ... ∧ An -> B 是重言式。
2.间接方法或反证法:证明 A1 ∧ A2 ∧ ... ∧ An ∧ ¬B 是矛盾式。
用上述转换的证明去推理的称之为简单证明推理。
采用的方法:
1.真值表(一般不用)
就是给命题公式赋值所有可能值,判断是否都为1
2.等值演算
通过等值演算,若公式(A1 ∧ A2 ... ∧ Ak) -> B ⇔ 1,则说明推理正确;否则推理不正确。
注意:下面的 |= 表示 ⇒。

3.主析(合)取范式
若公式(A1 ∧ A2 ... ∧ Ak) -> B 的主析取范式含全部2^n个极小项,则说明推理正确。否则推理不正确。

构造证明推理
基于永真蕴含式或推理规则进行的命题公式的推理称为构造证明推理。
下面列出一些基本的永真蕴含式/推理规则


直接构造证明推理:从一组已知的命题公式的前提出发,利用推理规则逐步推演出逻辑结论的推理。
间接构造证明推理:从一组已知的命题公式的前提以及附加的前提出发,利用推理规则间接地给出推理有效性证明的推理。
下面我用直接和间接分别证明。

命题符号化都是一样的。

先是直接构造证明推理
前提:
结论:
证明:(1) (2) ...
大家要按照这样的模版来写。

然后是间接构造证明推理
前提:
附加前提(原来结论(A->B)的A命题):
新的结论(原来结论(A->B)的B命题):
证明:(1) (2) ...

ps: 命题逻辑的旅途到此结束了,没点关注的点点关注,动动手手点点赞,再来一个收藏,咳咳,大家要是没看过集合论的可以去看看我写的离散数学——集合论-优快云博客,我们下期图论再见,Bye~Bye。




















 8961
8961

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








