数学建模boom的课程资料整理

数学建模boom的课程资料整理+自己整理的一些内容

一、优化类问题

• 有限的资源，最大的收益

• 三要素：决策变量+目标函数+约束条件

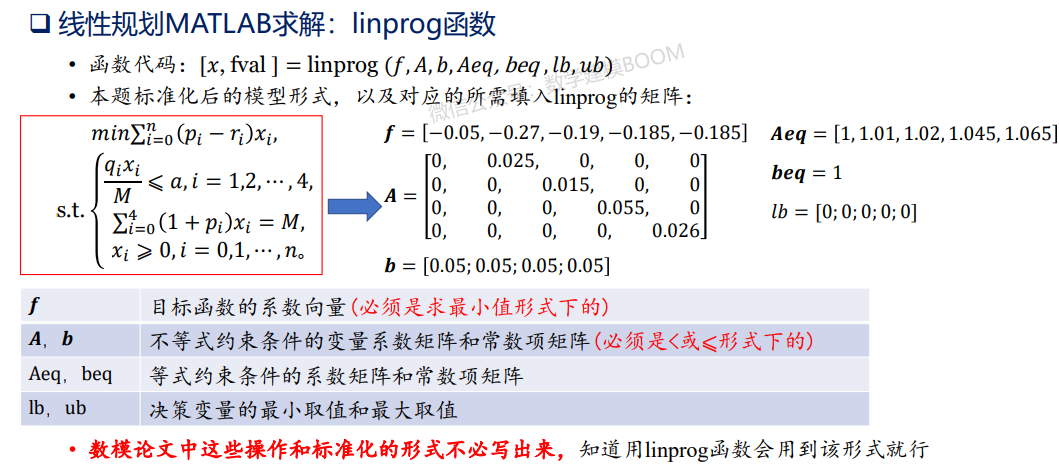
1-1线性规划-简介-适用赛题-原理与例题-代码求解LinearProgram.mlx

适用赛题：

• XXX有多少多少，怎样安排，分配，最多（少），利润最大
• 生产安排，总利润最大
• 投资收益：总收益最大
• 销售运输：总运费最省
• 车辆安排：车次安排最合理

总收益最大——一般是线性规划

总收益率最大——一般是非线性规划

建立留下的坑要在求解问题时填上！

1-2蒙特卡洛法MTKL.m

方法简介

注意不同问题有不同的概率分布：

如泊松分布、均匀分布

重点：

随机性、统计性、近似解

下面“非线性规划”会应用蒙特卡洛法求解典型例题的初始值

1-3非线性规划-简介-适用赛题-原理与例题-代码求解nolinear.mlx

求解方法：

利用matlab的fmincon函数

适用赛题

本质上和线性规划一样，适用于最优化

常见收益率、病毒传播率、经济增长率等涉及变量比值的规划问题

空间运动（如飞行管理、卫星轨道调整、还有和角度相关的电影院座位最佳视角问题）

选址问题（因为坐标点距离公式属于非线性）

注意

非线性规划每次求解的结果都不一样

1-4多目标规划-简介-适用赛题-模型原理与典型例题-代码求解 multiple_target.mlx

本质：

既要……又要……

模型简介

正偏差变量、负偏差变量

绝对约束（必须满足）、目标约束（允许有偏差）

优先因子

序贯算法

代码求解

注意多目标规划求得的叫做“满意解”而不是”最优解“

多目标规划没有最优的概念，因为在求解的过程中，三个目标的重要性的设定是具有主观性的

具体代码见multiple_target.mlx

二、最短路径和最小生成树

2-1图论的基本概念

好好反思一下自己数据结构和离散数学学得怎么样！

2-2单源最短路径-简介与适用赛题-原理-例题-代码求解shortestpath.mlx

适用赛题

货物运输类问题

设备更新问题：在一定年限内，如何安排购置新设备和使用旧设备，使总支付费用最小

典型特征

从某个起点到某个终点，始终围绕着起点到终点的总路径求最优

注意事项

图论解决的问题大部分都是求最优解，常常与规划类模型结合

2-3最小生成树-简介与适用赛题-原理-例题-代码求解minspantree.mlx

适用赛题

通信建设、管道铺设规划

对应图论，重点在于所有顶点两两之间都存在路径（连通），且总路径（权重之和）最小

最小生成树和最短路径之间的比较

• 最小生成树是从全局角度考虑，使两两之间连通且总路径最短，没有起点和终点的概念

• 最短路径是针对指定源点（起点）和指定终点，求两点间最短路径

三、综合评价问题

3-1层次分析法-简介与适用赛题-原理与例题-代码求解