详解Tarjan之割点【C++】【P3388 题解】

例题

P3388 割点

首先认识两个数组：

int dfn[N];
int low[N];

dfn[i] = 节点i的时间戳，就是第几个访问到该节点（子节点之间时间戳不同不影响结果）。

low[i] = 从节点i出发，不经过父节点能够回到的最早时间戳。

如下图所示（动图包含递归计算dfn和low的过程）：

如果你觉得太快了，请跳转附。

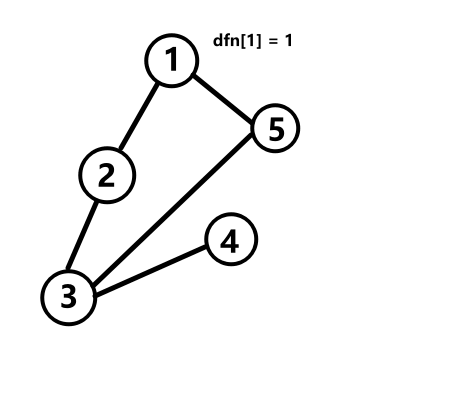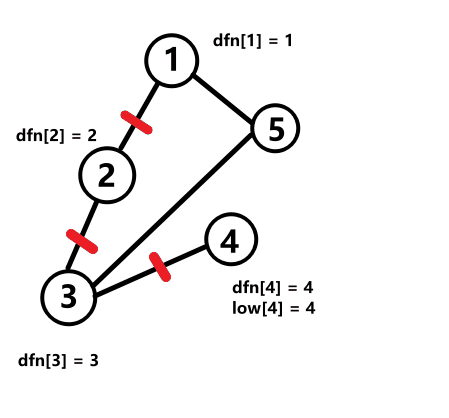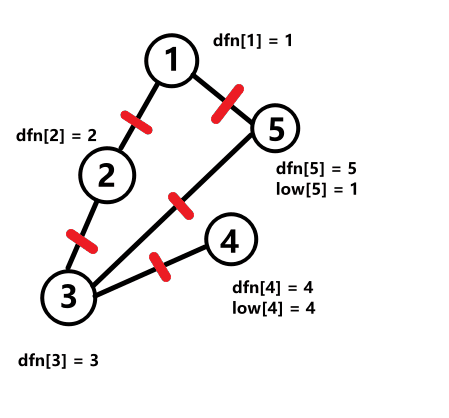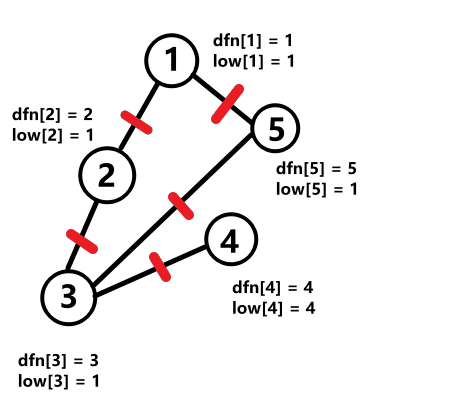
low怎么计算？

// v为u的孩子节点
1. 若 v 是未访问子节点：low[u] = min(low[u], low[v])
// 孩子能到哪 我就能到哪
2. 若 v 是已访问节点且非父节点：low[u] = min(low[u], dfn[v])

相信你已经明白dfn和low了。

判断是否为割点：

情况一：非根节点

如果子节点v无法通过其他路径绕过u访问u的祖先节点【即时间戳更小的节点】，说明u必不可少，是割点。

如下图所示（u是割点）：

if (low[v] >= dfn[u] && fa != -1) {
    isCut[u] = true;
}

情况二：根节点

如果根节点的子节点中【子连通块】数量（即移除根节点后剩下的连通块数量）大于等于2，它就是割点。

如下图所示（u是割点）：

（u不是割点）：

int child = 0;
for (int v : e[u]) {
    if (dfn[v] == 0) {
        child++;
        Tarjan(v, u);
        // ... 
    }
}
if (fa == -1 && child >= 2)
    isCut[u] = true;

完整代码

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;

const int N = 2e4 + 5;

int n, m, dfn[N], low[N], t = 0;
bool isCut[N];
vector<int> e[N];

void Tarjan(int u, int fa) {
    dfn[u] = low[u] = ++t;
    int child = 0;

    for (int v : e[u]) {
        if (dfn[v] == 0) {
            child++;
            Tarjan(v, u);
            low[u] = min(low[u], low[v]);

            // 非根节点且满足割点条件
            if (low[v] >= dfn[u] && fa != -1) {
                isCut[u] = true;
            }
        }
        else if (v != fa) {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (fa == -1 && child >= 2)
        isCut[u] = true;
}


int main() {
    cin >> n >> m;
    while (m--) {
        int x, y;
        cin >> x >> y;
        e[x].push_back(y);
        e[y].push_back(x);
    }
    for (int i = 1; i <= n; i++) {
        if (dfn[i] == 0)
            Tarjan(i, -1);
    }
            
    int cnt = 0;
    for (int i = 1; i <= n; i++) 
        if (isCut[i]) cnt++;
    cout << cnt << endl;
    bool f = false;
    for (int i = 1; i <= n; i++) {
        if (isCut[i] == true) {
            if (f) cout << " ";
            cout << i;
            f = true;
        }
    }
    return 0;
}

附