同余|欧拉定理|费马小定理|扩展欧拉定理|扩展欧几里得算法

同余

基本定理

欧拉定理

若a,m互质，则
\[ a^{\varphi\left ( m \right )}\equiv 1\left ( mod \ m \right ) \]

应用

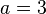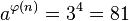令，，这两个数是互素的。比5小的正整数中与5互素的数有1、2、3和4，所以。计算：，而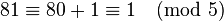。与定理结果相符。

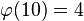计算的个位数，实际是求被10除的余数。7和10互素，且。由欧拉定理知。所以。

---

费马小定理

若p是质数，则对于任意整数a，都有
\[ a^{p}\equiv a\left ( mod \ p \right ) \]

---

扩展欧拉定理

\[ a^{b}\ mod \ m,若 b>=\varphi\left ( m \right ),则 \]

\[ a^{b} \equiv a^{b\ mod\ \varphi \left ( m \right )+\varphi\left ( m \right )}\left ( mod \ m \right ) \]

---

扩展欧几里得算法

搬到另一篇博客：

扩展欧几里得算法By Saitoasuka

转载于:https://www.cnblogs.com/saitoasuka/p/10335891.html