基于稀疏矩阵的WSN节能数据收集

基于稀疏随机矩阵的无线传感器网络中稀疏数据节能收集

XIAOHAN YU，浙江工商大学
SEUNG JUN BAEK，韩国大学

我们研究了在无线传感器网络中使用压缩感知（CS）收集稀疏数据时的能效问题。我们采用稀疏随机矩阵作为感知矩阵，称之为稀疏随机采样（SRS）。在SRS中，仅需一个被随机选中的节点子集（称为源节点）向汇聚节点上报数据。给定源节点后，我们旨在构建一棵数据聚集树，使得（1）该树以汇聚节点为根并覆盖所有源节点，且（2）数据收集完成后，树中节点的最小剩余能量最大化。我们首先证明该问题是NP完全的，然后设计了一个多项式时间算法来近似求解该问题。我们通过多轮次贪婪地构造一系列数据聚集树，并提出一种多项式时间算法以在每轮收集线性组合的测量值。我们证明所提出的算法具有可证明的近最优性。仿真和实验结果表明，所提出的算法不仅在提升最小剩余能量方面表现优异，而且有效延长了网络寿命。

CCS概念: •网络→传感器网络; 网络性能建模;

附加关键词和短语： 无线传感器网络（WSNs），数据收集，压缩感知（CS），能效，稀疏感知矩阵

ACM参考格式
余晓涵和白承俊．2017年．利用稀疏随机矩阵在无线传感器网络中节能地收集稀疏数据．计算机协会传感网汇刊．13卷，3期，文章22（2017年8月），36页．https://doi.org/10.1145/3085576

1 引言

在本文中，我们研究无线传感器网络（WSNs）中的数据收集问题（Lindsey 等 2002；Di Francesco 等 2011）。无线传感器网络被认为是物联网（IoT）架构中数据采集和感知的关键使能技术（Gubbi 等 2013；Perera 等 2014）。无线传感器网络由低成本、低功耗且能量受限的传感器组成，这些传感器通过无线链路将采集到的信息传输至汇聚节点（Akyildiz 等 2002；Bouabdallah 等 2009；Jongerden 等 2010；Cheng 等 2010）。影响无线传感器网络性能的一个主要限制因素是电池供电传感器的能量。当传感器耗尽其电池能量时，将停止工作。本文的目标是设计一种节能型数据收集策略。

提高能效的基本方法包括平衡传感器上的流量负载，例如Liang和Liu（2007年）、 Wu等（2010年）以及Stanford和Tongngam（2009年）提出的方法。一种提高能效的方法是构建生成树，以最大化节点的最小剩余能量。例如，Liang和Liu（2007年）研究了无线传感器网络(WSN)中处理多个查询的在线数据收集问题。他们提出了一种称为最大网络寿命（MNL）的贪心算法，以在每次查询响应后最大化节点的最小剩余能量。MNL从汇聚节点开始，迭代地将剩余能量最大的节点加入生成树中，并被证明在多种查询类型下表现良好。另一种方法是最大化网络网络寿命或传感器的最短运行时间，其中传感器的运行时间定义为能量耗尽前的时间。例如，Stanford和Tongngam（2009年）研究了结合数据聚合的网络寿命最大化问题。他们的方法结合了线性规划与最小代价树形图的精确计算。他们证明所提出的方法至少能达到最优网络寿命的（1 −ϵ）倍。Wu等（2010年）专注于通过构建生成树来均衡网络负载，从而最大化网络寿命。他们证明该问题是NP完全的，并提出了一种近似算法，该算法迭代地改进能量水平较低的节点。然而需要注意的是，在 Wu等（2010年）的研究中，假设汇聚节点从所有传感器进行数据聚合，且链路上的传输能耗在整个网络中是固定的。本文研究一个更一般化的问题：我们将考虑从任意子集的节点进行数据收集时，最大化最小剩余能量。此外，我们假设每条链路的能耗可能不同，以反映网络中链路质量的差异。

近年来，压缩感知（CS）（Donoho 2006；Baraniuk 2007；Candès和Wakin 2008）在无线传感器网络（WSN）领域引起了广泛关注（例如，Luo 等（2009）、Wang 等（2007）、 Ebrahimi 和 Assi（2014）、Karakus 等（2013）以及霍普特等人（2008））。压缩感知的核心思想是从显著较低维度的测量值中可靠地恢复高维信号（即原始数据向量）。Luo 等（2009）提出了压缩数据收集（CDG），利用压缩感知技术在无线传感器网络中进行数据收集。在CDG中，汇聚节点收集感知数据的线性组合，而非单个数据样本。一旦收集到足够数量的线性组合，汇聚节点便可通过求解基于ℓ1的凸优化问题来恢复原始稀疏数据向量（Eldar和 Kutyniok 2012）。CDG的主要优势在于不仅降低了传感器的能耗，而且使网络中的负载更加均衡。Wang 等（2007）提出了一类稀疏随机感知矩阵，这类矩阵不会影响数据恢复性能。在其方案中，每个节点将一次测量值聚合为原始数据的线性组合，如Luo 等（2009）所述。汇聚节点只需从任意m个节点收集这些测量值即可恢复原始数据。然而，在Wang 等（2007）的研究中，由于存在n个节点且每个节点聚合一次测量，因此聚合测量总数为n。这存在冗余，因为汇聚节点仅需m次测量即可完成恢复。Ebrahimi 和 Assi（2014）将Wang 等（2007）提出的稀疏随机矩阵应用于CDG，并提出了最小生成树投影（MSTP）方案。MSTP旨在通过构建多个最小生成树来最小化总能耗。每棵最小生成树以一个随机选择的节点为根，用于收集一次测量值。聚合后的测量值通过最短路径发送至汇聚节点。Karakus 等（2013）从网络寿命的角度比较了基于压缩感知的方案与无线传感器网络中的传统数据收集技术。他们表明，只要原始数据是稀疏的且网络满足一定条件，网络寿命便可显著延长。

稠密。然而，他们仅考虑了稠密感知矩阵，而我们采用稀疏感知矩阵以进一步改进能效。关于压缩感知(CS)在无线传感器网络中的应用的更全面综述，读者可参考Haupt等人（2008年）。

之前的所有研究都考虑了从每个节点进行数据收集（即生成树的构建）。然而，我们考虑的是从任意子集的节点进行数据收集。在早期的研究中，Fürer 和 Raghavachari （1994）提出了一种算法，用于构造一棵覆盖任意节点子集并最小化无权图中节点最大度的树。我们的设置比 Fürer 和 Raghavachari（1994）更通用，因为我们的目标是最大化加权图中节点的最小剩余能量。具体而言，我们考虑一种加权图，其中节点的能耗是与其相连边的权重的函数。此外，每个节点初始时可能在其电池中存储有不同的能量。我们的算法综合考虑了所有初始能量设置、节点的剩余能量以及边权重。

Contributions： 我们研究了使用稀疏随机采样（SRS）进行压缩数据的节能收集。目标是在数据向量的检索过程中最大化最小剩余能量；然而，由于源节点集合在多轮次中随机变化，该问题被证明是困难的。为此，我们采用一种逐轮贪心方法，即在每一轮中最大化最小剩余能量；具体而言，在每一轮中，我们的目标是构建一棵覆盖该轮所有相关源节点的数据收集树。我们首先证明，即使针对单轮的优化也是NP完全的。随后，我们提出了一种称为近似最大最小剩余能量斯坦纳树（AMREST）的多项式时间算法，用于为每一轮构建数据收集树。通过AMREST，我们迭代地寻找良好路径，从而避开剩余能量较低的传感器。我们证明AMREST具有可验证的高效性：（i）存在一个性能极限，任何多项式时间算法都无法在所有可能系统中普遍超越该极限；（ii）AMREST的性能可保证接近该极限，且差距仅为一个常数。在初始能量储备和链路通信成本在整个网络中均匀分布的特殊情况下，我们证明最优性差距为常数，与网络拓扑结构无关。仿真和实验结果表明， AMREST在最大化最小剩余能量以及延长网络寿命方面表现良好。

论文结构： 在第2节中，我们提出了稀疏随机采样，并给出了使用稀疏感知矩阵实现稳定恢复的三个示例。我们在第3节中对问题进行建模，并在第4节中提出AMREST。第5节提供了性能分析。在第6节中，我们展示了仿真结果。第7节给出了在无线传感器网络测试平台上的实验结果。第8节对全文进行总结。

2 稀疏随机采样(SRS)

我们首先简要介绍压缩感知(CS)技术。在压缩感知(CS)中，考虑以下线性模型：
$$ y= Ax, \tag{1} $$
其中，$y \in \mathbb{R}^m$是测量向量，$x \in \mathbb{R}^n$是数据向量，$A \in \mathbb{R}^{m\times n}$称为感知矩阵。如果向量$x$在基$\Psi$下满足$x=\Psi c$，且$c$中非零元素的个数不超过$k$，则称$x$为$k-$稀疏。假设$A$是一个高斯随机矩阵，即矩阵$A$的每个元素均从高斯分布$N(0, 1/m)$中独立同分布(i.i.d.)抽取。众所周知，如果$m = O(k \log(n))$且$k \ll n$，则可以通过线性规划以高概率恢复$k-$稀疏向量$x$（Candès和Wakin 2008；Eldar和Kutyniok 2012）。

考虑一个具有$n$个传感器的无线传感器网络(WSN)。传感器数据用$x$表示，其中第$j$个元素$x_j$表示网络中第$j$个节点的原始数据。在CDG中，汇聚节点根据以下方式收集数据

由公式(1)给出的线性模型，其中矩阵$A$ 是一个高斯随机矩阵。我们将第$i$轮定义为收集由下式给出的$y_i$的过程
$$ y_i= \sum_{j=1}^n a_{ij} x_j , \quad i= 1, 2,…, m, \tag{2} $$
其中$a_{ij}$表示矩阵$A$的第$i$行和第$j$列的元素。因此，总共进行$m$轮数据收集。以CDG下的数据收集为例：见图1(a)。汇聚节点将在$m$轮内收集$m$次测量值$y_1,y_2,…，y_m$。因此，每个节点传输$m =O(k \log n)$次。与收集每个单个测量值相比，CDG显著减少了网络负载并使其分布更加均匀，后者平均每节点需要$O(n)$次传输（Luo等人，2009年）。

最近，稀疏随机矩阵被证明具有与高斯随机矩阵相似的恢复性能（Wang 等人 2007年； Li 等人 2013年；Gilber 和 Indyk 2010年）。稀疏随机矩阵是指其元素以固定概率独立地为零的矩阵。重要的是，如果$a_{ij} = 0$，我们在收集$y_j$时将不需要数据$x_j$，因为$y_i$是由公式（2）给出的线性组合。也就是说，在第$i$轮中，我们只需要从那些$a_{ij}$非零的传感器收集数据。因此，通过使用稀疏随机矩阵，我们有效地随机选择节点进行数据收集。我们将这种选择称为稀疏随机采样（SRS）。被选中的节点称为源节点。图1中的示例比较了稀疏随机采样（SRS）和传统的CDG。在该示例中，SRS的感知矩阵由矩阵$A$给出
$$ A= \begin{bmatrix} a_{11} & 0 & 0 & a_{14} & 0 & a_{16} \ a_{21} & 0 & a_{23} & a_{24} & 0 & 0 \ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \ 0 & a_{m2} & a_{m3} & 0 & a_{m5} & 0 \end{bmatrix} . \tag{3} $$
在每一轮中，只有节点的一个随机子集传输数据，而传统的CDG是在数据收集期间每个节点都进行传输。这降低了与数据收集相关的能耗和延迟。在图1(b)示例的第一轮中，我们有$a_{12}=a_{13}=a_{15}= 0$；参见公式(矩阵A 中的第3)行。我们可以将非源节点（即节点2,3,和5）置为“睡眠”模式，从而进一步节省能量。同时，在第二轮中，节点6（图1(b)中的阴影节点）不是源节点（即$a_{26}= 0$），但被迫保持“唤醒”状态，以便源节点能够到达汇聚节点。

在大规模无线传感器网络中，如何在稀疏随机采样（SRS）下高效地在源节点和非源节点上收集数据是一个关键问题。我们的目标是构建一个数据收集树，该树不仅覆盖所有源节点，而且根据传感器的剩余电池容量，在整个网络中均衡分配网络负载，从而延长传感器的运行时间。本文中，我们的目标是在使用SRS完成数据向量$x$的采集后，最大化传感器中最小剩余能量。随后我们将证明，我们的方法在网络运行时间的延长方面也十分有效；例如，在不耗尽任何传感器电池的情况下，尽可能多地采集数据向量。据我们所知，与稀疏感知矩阵相关的最大化最小剩余能量问题尚未被研究过。

接下来，我们提供三种稀疏感知矩阵的示例，这些矩阵可保证原始数据向量$x$的稳定恢复。所有这些稀疏矩阵都是通过对矩阵$A$的元素以固定概率随机“稀疏化”得到的。这里，我们引入一个本文中广泛使用的关键参数，称为保留概率$s \in(0, 1]$，它表示矩阵$A$中某个元素非零的概率。

定理2.1 (Baraniuk等人，2008年). 假设原始数据向量$x \in \mathbb{R}^n$是$k$-稀疏的，并且感知矩阵$A$中的每个元素均独立地从该分布中抽取
$$ a_{ij} = \sqrt{1/m}\times \begin{cases} +1 & \text{with probability } s/2, \ 0 & \text{with probability } 1 - s, \ -1 & \text{with probability } s/2, \end{cases} $$
其中$s \in[ 1/3 , 1]$。那么，$A$具有与高斯随机矩阵相同的恢复性能；即，$m= O(k\log n)$足以保证对$x$的稳定恢复。

定理2.1意味着，平均而言，矩阵$A$中最多三分之二的元素可以为零，而不会影响恢复性能，因为$s$可以减小至$1/3$。

定理 2.2 （王等人，2007年）。假设原始数据向量$x \in \mathbb{R}^n$在基$\Psi$下$k$-稀疏且满足：
$$ \frac{|x| \infty}{|x|_2} \le h. $$
假设感知矩阵$A$中的每个元素均独立地从分布中抽取
$$ a {ij} = \sqrt{1/sm}\times \begin{cases} +1 & \text{with probability } s/2, \ 0 & \text{with probability } 1 - s, \ -1 & \text{with probability } s/2, \end{cases} \tag{4} $$
其中$s \in(0, 1]$，且测量值的数量满足
$$ m= \begin{cases} O\left( \frac{h^2k^2(1+\gamma)}{s\epsilon^2} \log n\right) & \text{if } h^2/s \ge\Omega(1), \ O\left( \frac{k^2(1+\gamma)}{\epsilon^2} \log n\right) & \text{if } h^2/s \le O(1), \end{cases} \tag{5} $$
其中 $\gamma$和$\epsilon$是两个正常数。然后，给定$y$，$A$和$\Psi$，可以得到一个估计值$\hat{x}$，使得 $|x -\hat{x}|_2^2 \le(1+ \epsilon)|x|_2^2$，其概率至少为 $1 -n^{-\gamma}$。

定理2.2适用于数据向量的峰值能量与总能量之比被参数$h$限定的情况。我们观察到，在定理2.2中，当$h^2/s \ge\Omega(1)$时，$m= O(k^2 \log n)$成立。回想一下，当使用高斯随机矩阵作为感知矩阵时，$m= O(k\log n)$。这意味着，若使用公式(4)中的矩阵作为感知矩阵，则为了保证稳定恢复，需要增加测量值的数量。

Li 等人(2013)提出了一类稀疏随机矩阵，该矩阵能以与高斯随机矩阵相同数量级的测量值$m= O(k\log n)$来保证稳定恢复。

定理2.3 （Li等人，2013）。假设原始数据向量$x \in \mathbb{R}^n$是$k$-稀疏且非负的。令$a_{ij}= b_{ij} q_{ij}$，其中$b_{ij}$是从单位尺度的 $\alpha$-稳定最大偏斜分布中独立同分布地抽取的，且$q_{ij}$满足
$$ q_{ij}=\begin{cases}1 & \text{with probability } s, \ 0 & \text{with probability } 1 - s, \end{cases} \tag{6} $$
其中$s \in(0, 1]$。然后，给定$y$和矩阵$A$，使用$m= k \log(n/\epsilon) / (1-e^{-(1-s)k})$测量值就足以以至少$1 -\epsilon$的概率实现对$x$的恢复，且误差任意小。

我们观察到$m= O(k\log n)$如果$s=\Theta(k^{-1})$；也就是说，可以仅从$\Theta(k^{-1})$比例的节点收集数据，而不会降低恢复性能。在定理2.3中，要求数据向量为非负，这适用于实际中的许多类型的信号（例如，有界信号可以转换为非负信号（Li 等人 2014年））。前述任意矩阵均可用于稀疏随机采样；然而，我们将提出一种可用于任意$s \in(0, 1]$的算法（下文将详述）。

在本文中，我们假设原始数据向量在某个基上是稀疏的。在实际实现中，使数据向量在某个基上变得稀疏是一个非平凡的问题。尽管这类稀疏化技术超出了本文的范围，我们将简要提及一些相关问题。Quer 等人（2009年）的早期工作研究了稀疏化问题。在通过路由对传感器数据进行随机投影与信号的稀疏表示之间实现不相关性并不直观，而这种不相关性是压缩感知恢复所必需的。作者考虑了多种流行的变换方法，发现没有一种方法能够同时对实际数据集实现稀疏化，并且与路由矩阵保持不相关性。随后，作者在 Quer 等人（2012）中提出了一种称为 SCoRe1 的稀疏化框架。SCoRe1 能够通过利用可估计信号重构误差的反馈控制环，有效地自适应实时数据向量。SCoRe1 的关键技术是使用主成分分析（PCA）来捕获无线传感器网络(WSN)测量的实际数据向量的时空特性。他们的研究表明，在某些统计假设下，通过对传感器数据进行类似于稀疏随机采样(SRS)的随机采样，然后结合使用压缩感知与PCA进行恢复，将压缩感知用于无线传感器网络中的数据收集是合理的。

3 问题描述

考虑一个加权图$G=(V,L)$，其中$V:={v_1,v_2,\dots,v_n}$是包含汇聚节点$v_1$的节点集合，$L$是边集合。每条边$l \in L$通过函数$w:L\to[\alpha, \beta]$被赋予一个权重，其中$0< \alpha \le \beta$。这些权重与我们的能耗模型相关，稍后将进行说明。回顾我们的目标是在完成数据向量$x$的收集后，最大化最小剩余能量。为了获取$x$，我们需要总共收集$m$次测量。记$S_i$为第$i$轮的源节点集合。换句话说，$S_i$包含那些第$i$个系数非零的节点；即$S_i:={v_j: a_{ij} \ne 0}$，其中$a_{ij}$是节点$v_j$的第$i$个系数。第$i$轮的数据收集树表示为$T_i=(V_{T_i},L_{T_i})$，其中$V_{T_i} \subseteq V$是$T_i$中的节点集合，$L_{T_i} \subseteq L$是$T_i$中的边集合。

矩阵$A$中的随机系数应为网络所知。然而，将矩阵$A$的所有元素分发到整个网络存在实际问题，可能会导致显著的通信开销。稍后，我们将介绍一种利用伪随机数生成器（PRNG）来最小化此类开销的方法。

我们假设所有节点（包括汇聚节点）都使用相同的PRNG。在网络初始化时执行以下过程：
—汇聚节点为PRNG生成一个种子，记为$c$。注意，种子是用于初始化PRNG的一个数值。
—汇聚节点将$c$广播至整个网络。
—每个传感器通过将其自身节点ID与汇聚节点的种子结合（例如，将种子与ID进行拼接）来生成各自的种子。
—用$c_i$表示节点$i$的种子。在第$j$轮中，节点$i$将使用以种子$c_i$初始化的PRNG生成矩阵$A$的随机系数$a_{ji}$。

请注意，种子$c_i, i= 1,\cdots,n$为网络所知，这使得每个节点都能与其他节点生成相同的随机数集合。因此，在整个数据聚合的轮次中，感知矩阵$A$对网络是有效已知的。通信开销仅在于广播$c$，因此仅在系统初始化时存在。在数据收集期间，汇聚节点将在第$i$轮开始时计算并广播树$T_i$的路由信息给每个节点。树$T_i$中的节点$v_j$将生成$a_{ji}$作为其系数。在接收到来自其在$T_i$中所有子节点的数据后，$v_j$将其接收到的数据与自身数据$a_{ij}x_j$进行线性组合，并将结果传输给其父节点。注意，若$v_j$是源节点，则$a_{ij} \ne 0$；若$v_j$不是源节点，则$a_{ij} = 0$。

接下来我们介绍能耗模型。记 $I:={I(v_1)，I(v_2)，\cdots，I(v_n)}$为初始能量集合，其中 $I(v_j)$表示节点$v_j$的初始能量。我们假设汇聚节点是一个特殊节点，具有无限的初始能量（即$I(v_1)= \infty$）。假设每个节点通过大小为$b$比特的数据包传输数据。此外，我们假设通过一条边传输和接收一比特数据所消耗的能量大致相等（Raghunathan 等人，2002年）。尽管这是对能量消耗的一种简化模型，但我们可以通过将每条链路不同的能耗成本反映到边权重上，从而捕捉节点之间不同的信道特性。具体而言，节点$v_i$通过链路$l=(v_i,v_j)$向节点$v_j$传输一比特数据时消耗$r_l$的能量；节点$v_j$从节点$v_i$接收一比特数据时也消耗相同数量的能量$r_l$。因此，节点$v_i$通过边$l=(v_i,v_j)$向节点$v_j$传输一个数据包时消耗$br_l$的能量，而节点$v_j$从节点$v_i$接收一个数据包时消耗$br_l$的能量。对于任意$l \in L$，记$w(l)=br_l$。那么，给定一棵数据收集树$T=(V_T,L_T)$，当数据通过$T$进行收集时，节点$v$消耗的能量为$\sum_{l \in L_v \cap L_T} w(l)$。本文所使用的符号说明总结于表1。

符号	说明
$G(V,L)$	网络图，其中$V$是节点集合，$L$是边集合
$V_T, L_T$	树$T$中的一组节点，树$T$中的边的集合
$S_i$	第$i$轮的源节点集合
$I$	初始能量集合，即$ I:={I(v): v \in V}$
$l_v$	与节点$v$关联的边
$L_v$	与节点$v$关联的边集合
$l_v^\dagger$	与$v$关联且具有最大权重的边，即$l_v^\dagger:={l_v \in L_v: w(l_v) \ge w(l’_v), \forall l’_v \in L_v}$
$T_m$	用于数据收集的$m$棵树的集合
$T(S)$	满足以下条件的树的集合：（1）$T$ 跨越 $S$；（2）所有叶节点$T$位于$S$中
$D(G,v)$	节点$v$在图$G$中的度
$E(T,v)$	若数据通过$T$收集，节点$v$的剩余能量
$R(T)$	在$T$中节点的最小剩余能量
$T(p)$	连接路径$p$的两个端点的路径在$T$中
$F(v)$	森林$F$中包含节点$v$的组件
$F(p)$	路径$p$中每个节点$v$的组件$F(v)$的并集，即$F(p)= \cup_{v\in p}F(v)$
$s$	保留概率

目标是找到一个集合 $T_m={T_1,T_2,…，T_m}$，使其最大化矩阵$A$的最小剩余能量：
$$
\text{(P0)} \quad \maximize_{T_m}
R(T_m),
$$
subject to $S_i \subseteq V_{T_i}$, $i= 1, 2,…, m$.
其中，$R(T_m) :=\min_{v\in V} E(T_m,v)$，$E(T_m, v)$表示通过$T_m$中的树收集测量值后节点$v$的剩余能量。(P0)很难求解；例如，我们将在后面证明即使对于$m= 1$，(P0)也是NP‐完全的。因此，我们采用一种贪心方法，在每一轮中尝试最大化最小剩余能量。具体而言，给定$S_i$，我们将构造一棵树$T_i$，满足$S_i \subseteq V_{T_i}$，以最大化$T_i$中节点的最小剩余能量。梁和刘 (2007)在不同背景下也采用了类似的贪心方法；他们的目标是在不耗尽任何节点能量的情况下，最大化无线传感器网络回答的查询数量。他们还提出针对每次数据收集查询，贪心地最大化节点的最小剩余能量。该方法的概要如算法1所示。

虽然这种贪心近似在实践中可能表现尚可，但其最优性差距可能显著。例如，当我们在每一轮中贪心地最大化最小剩余能量时，可能会导致消耗的总能量过多，从长远来看这会对网络造成负担。这可以通过限制网络在每一轮中消耗的总能量来部分缓解。我们将在第4.5节中详细讨论此问题。我们方法的另一个乐观方面是轮数最多为$m= O(k^2 \log n)$。因此，我们预计我们的近似解与问题(P0)的解之间的差距随网络规模$n$的增加而相对缓慢地增长。

接下来，让我们考虑单轮次中数据收集树的构建。不失一般性，我们考虑第$i$轮，并令$S:= S_i$。我们将构造一棵树$T=(V_T ,L_T)$，该树跨越$S$。记$D$将节点$v$在应用$T$进行数据收集时的剩余能量记为$E(T,v)$。我们有 that
$$
E(T, v)= I(v) - \sum_{l \in L_T \cap L_v} w(l). \tag{7}
$$
我们的目标是找到一棵树$T \in T(S)$，使得树$T$中节点的最小剩余能量最大化：
$$
\text{(P)} \quad \maximize_{T \in T(S)}
R(T):= \min_{v\in V_T} \left[ I(v) - \sum_{l \in L_T \cap L_v} w(l) \right].
$$

定理3.1. (P)是NP完全的。

证明。 见附录A。

T本文其余部分致力于开发一种算法，以近似求解(P).

4 所提出的算法

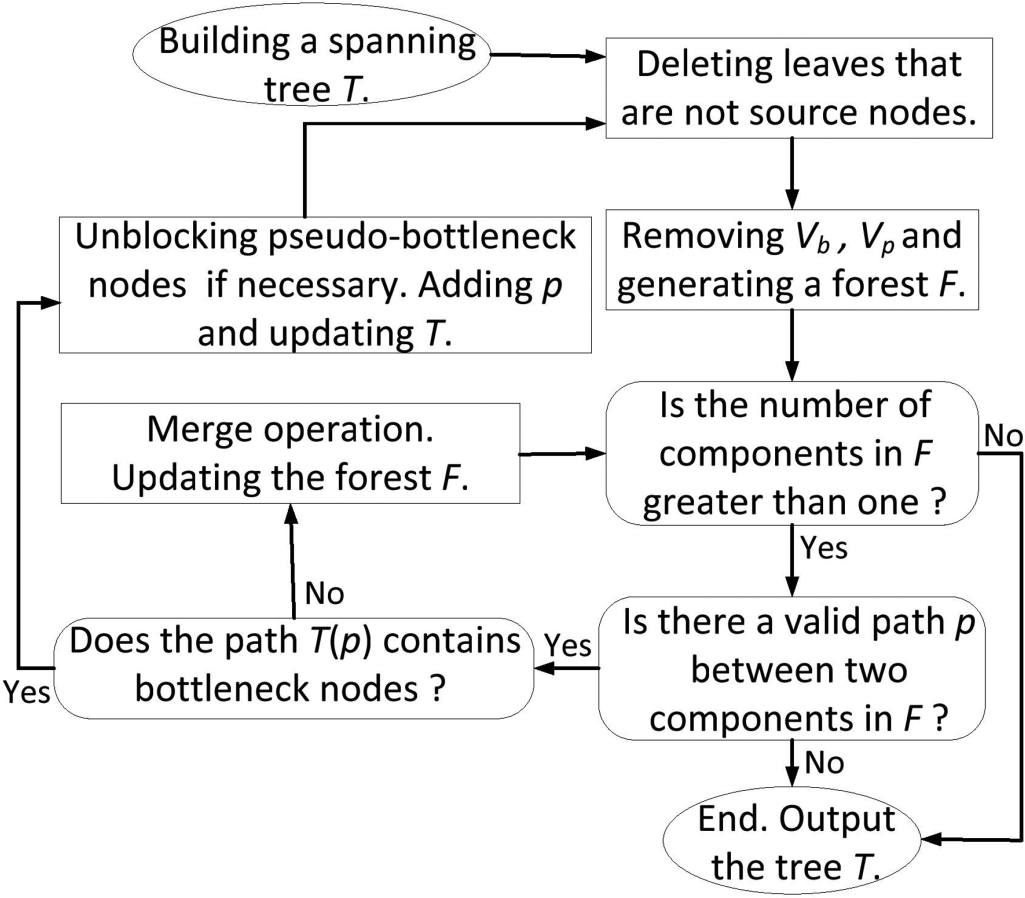
我们算法的关键思想是反复降低剩余能量较小的节点的负载。具体而言，我们首先构建一棵随机树$T \in T(S)$。接着，在树中寻找一条路径$p$，该路径上的所有节点均不在$T$中，除了端点之外，通过添加路径$p$并删除$T$中连接该节点的一条边，从而降低具有较小剩余能量节点的负载。此过程重复进行，直到无法再找到能够“改进”剩余能量较小节点的路径为止。

4.1 基本概念

我们首先介绍与所提出的算法相关的基本概念。其中一些概念借鉴自Fürer和Raghavachari （1994）以及Wu等人（2010年），我们对其进行了修改和推广，以适应我们的模型。给定任意一棵树$T=(V_T, L_T)$，我们将 $V_T$划分为三个互不相交的子集，如下所示：
—$V_b(T)={v \in V_T: R(T) \le E(T, v) < R(T) + w(l_v^\dagger)}$。$V_b$是那些剩余能量接近$T$中节点最小剩余能量的节点集合。$V_b$中的节点称为瓶颈节点。
—$V_p(T)={v \in V_T: R(T) + w(l_v^\dagger) \le E(T,v) < R(T) + 2w(l_v^\dagger)}$。$V_p$中的节点称为伪瓶颈节点。这些节点接近于成为瓶颈节点。
—$V_s(T)={v \in V_T: E(T,v) \ge R(T) + 2w(l_v^\dagger)}$。矩阵$A$中属于$V_s(T)$的节点称为安全节点。安全节点具有相对较大的剩余能量。

我们将不在$T$中的节点划分为两个互不相交的子集：$V_c(T)$和$V_{nc}(T)$。
—$V_c(T)={v \in V \setminus V_T: I(v) \ge R(T) + 3w(l_v^\dagger)}$。$V_c$中的节点称为候选节点。候选节点具有充足的剩余能量，用于减轻瓶颈节点的负载。
—$V_{nc}(T)={v \in V \setminus V_T: I(v) < R(T) + 3w(l_v^\dagger)}$。$V_{nc}$中的节点称为非候选节点。

我们简要说明候选节点的使用方法。考虑一条路径$p$，其中$T$中两个节点之间的所有中间节点均为候选节点。假设$p$为$(x, v_1,\dots,v_k, y)$，其中$x,y \in V_T$，而$v_1,\dots,v_k$为候选节点。假设我们将$p$加入$T$，并删除边$(x, v_1)$以生成一棵新树。由于$p$是一条路径，因此在$T$中任何候选节点的度最多为2，故路径$p$中的任何中间节点都不会成为瓶颈节点。因此，候选节点$v_i(i=1,\dots,k)$的剩余能量最多减少$2w(l_{v_i}^\dagger)$。根据定义，$v_i$的剩余能量至少为$R(T)+ w(l_{v_i}^\dagger)$。因此，$V_c(T)$是可在这种修改过程中安全添加到$T$中的节点集合。注意，在本文中，我们删除边$(x, v_1)$或$(v_k, y)$。这些增广路径将用于减轻瓶颈节点的负载，具体细节将在后文详述。综上所述，我们有$V_T \subseteq V_b \cup V_p \cup V_s$且$V \setminus V_T \subseteq V_c \cup V_{nc}$。

基于上述节点划分，我们引入以下概念:
— 有效路径 ：如果路径$p=(u, h_1,h_2,\dots, h_k, v)$的端点$u, v \in V_s \cup V_p$且$h_1,h_2,\dots, h_k \in V_c$（即端点为伪瓶颈节点或安全节点），而所有中间节点均为候选节点，则称该路径为有效路径。一条有效路径可能仅包含两个节点（例如，$p=(u, v)$），此时它退化为$L$中的一条边。
— 改进 ：假设$p=(u,\dots, v)$是一条有效路径，且$T(p)$包含一个瓶颈节点或伪瓶颈节点$b$。我们通过将$p$加入$T$并删除$T(p)$中与$b$关联的一条边来降低$b$的能耗。我们将此类修改称为改进，并称通过添加$p$改进了$b$。
— 阻塞 ：假设$p=(u,\dots, v)$是一条有效路径，且$T(p)$包含一个瓶颈节点$b$。同时假设将$p$加入$T$后使得$u$（或$v$或两者）成为瓶颈节点。在这种情况下，我们称$u$（或$v$或两者）从$p$阻塞了$b$。注意，只有伪瓶颈节点才可能阻塞$b$。
— 解除阻塞 ：为了改进被伪瓶颈节点$u$阻塞的瓶颈节点$b$，我们需要先降低$u$的能耗，然后再改进$b$。我们将降低$u$能耗的过程称为解除阻塞过程。解除阻塞过程的详细内容将在第4.4节中讨论。

我们将基于这些概念描述所提出的算法。

4.2 概述

在本小节中，我们

4.3 示例

考虑图3(a)中所示的图，其中$s_1$为汇聚节点。图3(a)显示了初始树$T$，其中每个叶节点均为源节点。节点$h_1$和$h_2$不在$T$中，因此是候选节点。假设节点$b_1 , b_2$和$u_2$的初始能量如下：
$$ I(b_1)= I(b_2)= 4, \quad I(u_1)= 7. $$

假设剩余节点的初始能量足够大，则$b_1, b_2,u_1$的剩余能量由以下给出
$$ E(T, b_1)= 1, \quad E(T, b_2)= 0, \quad E(T, u_1)= 3, $$
其中我们有$R(T) = E(T,b_2) = 0$。

我们将解释一次外层循环（第4–28行）。我们从$T$中移除$V_b \cup V_p$并生成森林$F$，该森林包含组件${s_1}$、${s_2}$、${s_3}$和${s_4}$：见图3(b)。在第9行的第一次while循环迭代中，我们找到一条在${s_2},h_1, s_3}$之间的有效路径$p_1=$，连接${s_2}$和${s_3}$。由于在$T(p_1)=(s_2,u_1, s_3)$中不存在瓶颈节点，我们将所有包含$T(p_1)$中节点的组件（即${s_2}$和${s_3}$）与$T(p_1)$合并为一个单一组件（第18行）：见图3(c)。此时森林中有三个组件：${s_1}$、${s_4}$以及${s_2,u_1, s_3}$。

接下来，我们迭代第9行的第二次while循环。我们在${s_2,u_1, s_3}$和${s_4}$之间找到一条有效路径$p_2=(u_1,h_2, s_4)$。在$T(p_2)$中存在两个瓶颈节点；因此，我们进入第13行。我们选择改进$b_2$，因为它比$b_1$具有更小的剩余能量。然后我们发现添加$p_2$会将$u_1$的剩余能量从3减少到1，这使得$u_1$成为一个瓶颈节点（即$u_1$阻塞了$b_2$来自$p_2$）。因此，我们首先通过添加$p_1$并删除$(u_1,s_3)$来改进$u_1$（即解除$u_1$的阻塞）：见图3(d)。注意，我们选择删除$(u_1,s_3)$，因为其权重为2，大于$(u_1,s_3)$的权重1。最后，我们通过添加$p_2$并删除$(b_2,s_4)$来改进$b_2$。这是一个解阻塞的简单示例；一般的解阻塞过程将在下一小节中详细说明。新的树$T_1$如图3(e)所示。因此，$R(T_1) = E(T_1,b_1) = 1$；因此，在AMREST的一次迭代后，最小剩余能量从$R(T) = 0$增加到$R(T_1) = 1$。

4.4 解除阻塞过程

在AMREST的第14行中，我们可能需要解除阻塞$u$或$v$。在本小节中，我们将解释解阻塞过程的详细信息。我们将把节点度最小化中的解除阻塞技术扩展到加权图的剩余能量优化情况。

4.5 缓解贪心方法的低效率

我们的贪心方法在每轮中最大化最小剩余能量，但可能存在有害影响。AMREST试图通过迭代扩展可能较长的路径到树中来改进瓶颈节点。这些长路径可能会导致网络中的能耗过高，从长远来看，经过多轮后可能产生不利影响。Li等人（2001）提出了一种新框架来缓解这一问题。作者提出了$max-minzPmin$算法，该算法寻找两个节点之间的路径，以最大化路径上的最小剩余能量。$max-minzPmin$的一个显著特点是，该算法探索了总能耗与最小剩余能量之间的权衡，其中总成本定义为边权重之和。具体而言，$max-minzPmin$在结果路径的总成本不超过$zPmin$的约束下，最大化最小能量。这里，$z \ge 1$是一个参数，$Pmin$是节点间的最小总成本。

受最大$-minzPmin$框架的启发，我们对AMREST进行如下简单修改：
（1）最初，我们通过使用例如Robins和Zelikovsky（2000年）中的算法，构建一棵覆盖源节点的近似最优斯坦纳树。AMREST过程将采用该树，而非算法2第4行中的初始化。用$C^ $表示该树的总能耗。$z \ge 1$是一个给定的参数。（2）在算法2第4行循环开始时，检查当前树的总成本是否超过$zC^ $。（3）如果超过，则终止该过程，并输出上一轮循环得到的树；否则，继续执行循环。

请注意，我们首先通过初始构建一个近似最优的斯坦纳树，获得近似的最小成本$C^ $。由于步骤（2）的存在，算法在将有效路径添加到树之前会检查总成本是否超过$zC^ $。因此，改进的AMREST保证输出树的总能耗最多为$zC^*$。因此，改进算法使我们能够在可能的最小总成本与最小剩余能量之间取得平衡。注意，$z$可以通过类似Li等人（2001）中提出的方法，在轮次中自适应地确定。

5 算法分析

我们首先分析AMREST的性能。设$R(T^*)$为第4节中定义的(P)的最优解。记$I_{max}$和$I_{min}$分别为$I$中的最大和最小初始能量。

定理5.1. 对于具有任意源节点集合$S \in V$和初始能量设置$I$的任意加权图，AMREST的输出$T$覆盖$S$并满足
$$
R(T) \ge R(T^*) -(2\beta+ \alpha+(\beta -\alpha)\Delta(G)+ I_{max} - I_{min}), \tag{8}
$$
其中$\Delta(G)$表示矩阵$A$的$G$的最大度。

证明。 见附录D。

定理 5.2. 假设存在一个多项式时间算法，使得输出$T’$满足
$$
R(T’)> R(T^*) -{\beta+(\beta -\alpha)\Delta(G)+ I_{max} - I_{min}} \tag{9}
$$
对于具有任意源节点集合$S$和初始能量设置$I$的任意加权图$S$和初始能量设置$I$。我们由此得到$P=NP$。

证明。 见附录F。

定理5.1表明，AMREST与最优解之间的最小剩余能量差距取决于最大度和初始能量设置。结合定理5.1和5.2，我们可以得出以下结论。设$T$表示AMREST的输出树。如果存在一个多项式时间算法，能够输出$T’$使得
$$
R(T’) - R(T)> \alpha+ \beta \tag{10}
$$
对于任意加权图以及任意的源节点和初始能量设置，若$P=NP$，则任何多项式算法在所有网络图和初始能量配置上的性能均无法比AMREST超出$\alpha+ \beta$，除非$P=NP$。该结果表明，可能存在在某些初始能量和网络设置下优于AMREST的算法；然而，很难找到一种在所有系统上均比AMREST性能优越超过一个常数的通用算法。我们在“均匀”设定下得到了关于AMREST性能的一个更强结论，其中初始能量设置和边权重均相同。以下推论是定理5.1和5.2的直接结果。

推论1. 假设$I_{max}=I_{min}$且$\alpha= \beta$。令$T$和$T’$分别表示AMREST和任意多项式时间算法的输出。除非$P=NP$，对于任意给定的图和源节点集合，以下成立：
$$
R(T) \ge R(T’) - 2\beta. \tag{11}
$$
换句话说，AMREST的性能接近最优，且与网络规模无关，其最优性差距是一个常数。

接下来，我们分析AMREST的计算复杂度。在每次外层循环（第4–28行）中，一个瓶颈节点$b$得到改进，并且一些候选节点被添加到$T$中。节点$b$的剩余能量至少增加到$R(T)+ \alpha$。对于一个安全节点或新加入的候选节点$v$，其剩余能量至少为$R(T)+ w(l_v^\dagger)$。考虑一个伪瓶颈节点$u \in V_p(T)$，其剩余能量在该循环期间发生了变化。可能出现两种情况：
—$u$的度保持不变。换句话说，在与$u$关联的边中，删除了一条属于$T$的边，并添加了一条不属于$T$的边。因此，$u$的剩余能量最多减少了$w(l_u^\dagger) -\alpha$。根据伪瓶颈节点的定义，$u$的剩余能量至少为$R(T)+ \alpha$。
—$u$的度增加1。这意味着添加了一条不属$T$但与$u$关联的边，并且在添加该边后，$u$仍然是一个伪瓶颈节点。因此，$u$的剩余能量至少为$R(T)+ w(l_u^\dagger)$。

因此，节点$u$的剩余能量至少为$R(T)+ \alpha$。综上所述，对于在外层循环中剩余能量发生变化的任意节点，其在外层循环结束后的剩余能量至少为$R(T)+ \alpha$。因此，在$|V_b(T)|$次循环后，最小剩余能量至少为$R(T)+ \alpha$。换句话说，在$|V_b(T)|$次循环后，最小剩余能量至少增加了$\alpha$。在最坏情况下，$T$中有$O(n)$个瓶颈节点，且$R(T)= 0$，$I(b)=I_{max}$，这导致了$O( I_{max}/\alpha \cdot n)$次外层循环。

然后我们评估每个外层循环（第4–28行）的复杂度。第5行和第6行的复杂度均为$O(n)$。在第10行中，检查$u$和$v$之间是否存在有效路径可以按如下方式实现。给定图$G=(V,L)$，令$G’=(V_c,L_c)$为由候选节点导出的子图。设$F’ i$为$G’$中的第$i$个组件。对于节点$u \in V_b \cup V_p$，记$C(u)$为$G’$中与$u$相连的组件集合；即$C(u)={i: \exists(u,x) \in L,\forall x \in F’_i}$。当且仅当$C(u) \cap C(v) \ne \emptyset$时，$u$和$v$之间存在一条有效路径。在最坏情况下，为所有$u \in V_b \cup V_p$构造$C(u)$的复杂度为$O(|L|)$。算法3的复杂度为$O(n)$，因为最多有$n-1$ while循环迭代。在第14行，算法3在每次外层循环中仅被调用一次。在第18行，我们在每次while循环迭代期间应用Tarjan的并查集算法来构建森林，其复杂度为$|L|A^{-1}(|L|,n)$，其中$A^{-1}(|L|,n)$是反阿克曼函数（弗勒和拉加瓦查里1994；塔扬1975；科曼等2009）。因此，每次外层循环的复杂度为$O(|L|A^{-1}(|L|,n))$。综上所述，AMREST的复杂度为$O(I {max}/\alpha \cdot |L|nA^{-1}(|L|,n))$。

6 仿真

本节中，我们通过数值方法评估AMREST的性能。我们使用MATLAB软件模拟数据聚合及其相关的能耗。传感器节点均匀且随机地部署在一个单位正方形区域内。汇聚节点位于右上角。我们假设当两个节点之间的距离不超过0.5时，它们之间存在一条边。每个节点具有相同的初始能量（100焦耳）。每条边的权重独立且均匀地从范围[1, 10]中抽取。我们将如下定义仿真中使用的网络寿命。

定义6.1。 考虑一个由$n$维数据向量$x^{(1)}$、$x^{(2)}$、$\cdots$组成的序列。我们将网络的网络寿命定义为在该网络中任意节点耗尽其能量之前所收集到的被检索的数据向量的数量。

我们首先考虑特殊情况$s= 1$（即矩阵$A$为稠密的情况）。当$s= 1$时，稀疏随机采样方案退化为传统的CDG；因此我们设$m= k\log n$，其中$k= \log n$。作为基准方案，我们考虑MST方案，其中每轮使用MST作为数据收集树。我们还将与MNL方案（Liang和Liu 2007年）进行比较。在MNL方案中，数据收集树初始仅包含汇聚节点。在每次迭代中，从尚未加入树的所有节点中选择剩余能量最大的节点加入树中，该过程重复直至所有节点都被包含进树中。图5比较了$s= 1$时的最小剩余能量。图中绘制的最小剩余能量已相对于初始能量进行了归一化处理。对于固定的$n$值，我们运行100次仿真，并在收集完$m$个测量值后计算平均最小剩余能量。我们观察到AMREST优于其他方案，与MST和MNL相比，最小剩余能量分别提高了11–45%和2–7%。我们发现，随着$n$的增大，最小剩余能量逐渐降低。这是因为$m$（每个节点的传输次数）随$n$的增加而增加。此外，我们观察到AMREST和MNL的最小剩余能量随$n$的增长下降速度明显慢于MST。这是因为AMREST和MNL都试图在节点间均衡剩余能量。然而，与MNL相比，AMREST在网络规模增大时，最小剩余能量的下降更为平缓。

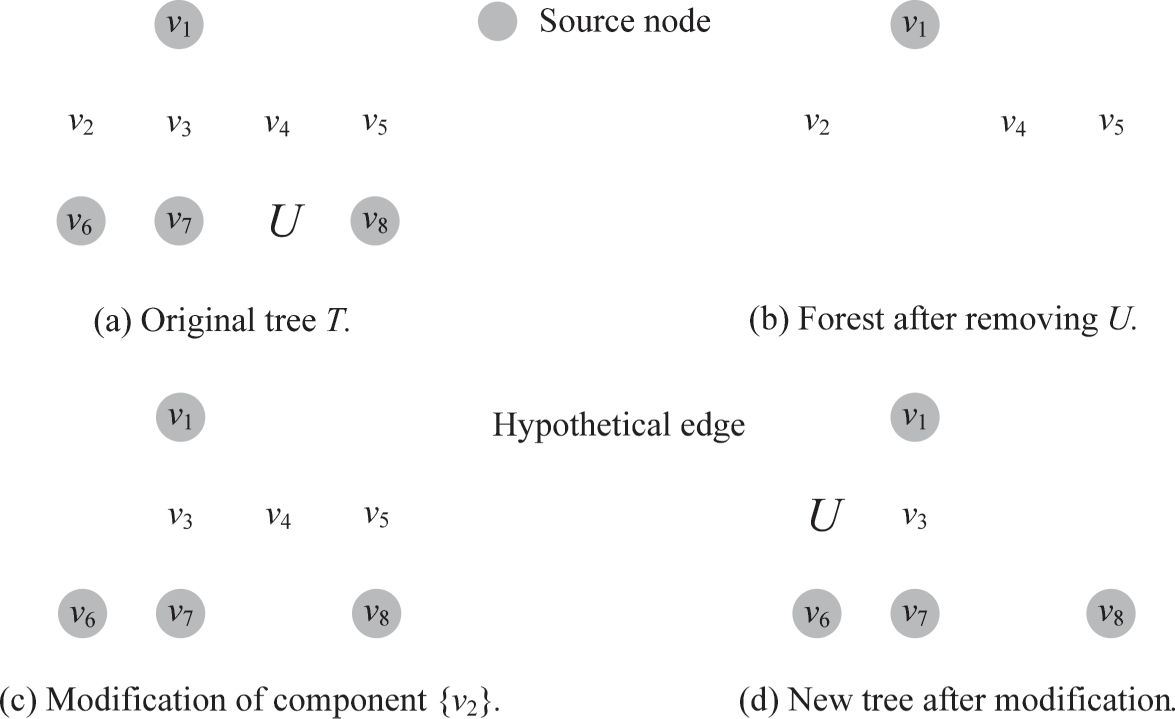
图6比较了$s= 1$时的网络寿命。我们观察到，AMREST的网络寿命与GK算法（Stanford和Tongngam 2009年）非常接近，该算法专门用于直接最大化网络寿命，其近似比为$(1 -\epsilon)$。但需要注意的是，GK算法仅适用于$s= 1$的情况。我们观察到，AMREST相对于MST和MNL分别将网络寿命最多提高了123%和42%。这表明，我们的算法通过在多轮次中迭代最大化最小剩余能量，同样在延长网络寿命方面非常有效。

接下来，我们比较$s< 1$的性能。我们将比较AMREST和如下定义的改进的MST方案。在改进的MST中，首先构造一个最小生成树，然后反复删除非源节点的叶节点，直到所有叶节点都是源节点。需要注意的是，当$s< 1$时，我们无法将AMREST与MNL或GK进行比较，因为这些算法是为情况$s= 1$设计的。

图7显示了当$s= 0$、$n= 100$和$m= 10$时，最小剩余能量的分布情况。我们观察到，AMREST的最小剩余能量明显大于改进的MST。此外，我们还观察到，AMREST的分布方差显著小于改进的MST。这意味着剩余能量的偏差关于源节点的随机选择，AMREST的变化更小。因此我们得出结论：与改进的MST相比，AMREST的性能对源节点的选择不那么敏感。图8比较了AMREST与改进的MST之间网络寿命比率的分布情况，其中$s= 0.5, n= 100,$和$m= 10$。我们观察到，AMREST实现的网络寿命至少比改进的MST方案大60%。此外，网络寿命的增益最高可达115%。

图9和10分别比较了最小剩余能量和网络寿命随保留概率$s$的变化情况。在图$n= 100$，$m= 10$中设置为图9所示，在图$n= 100$，$m= 1$中设置为图10所示。我们观察到，AMREST将最小剩余能量和网络寿命分别提高了22–37%和102–188%。我们还观察到，随着$s$的增加，最小剩余能量和网络寿命均呈下降趋势。这是因为当$s$较大时，每轮数据收集中需要更多节点参与。此外，我们观察到AMREST的网络寿命在$s$较小时随$s$的增大而下降得更快。较小的$s$意味着网络中每轮的平均源节点数较小。因此，为了维持网络连通性，必须将大量非源节点纳入数据收集树中。现在假设我们略微增加$s$，这可以通过假设通过将一些随机选择的非源节点提升为新的源节点来实现。如果$s$较小，则这些新源节点很可能不与其它源节点相邻。因此，需要向数据收集树中添加相对较多的非源节点，以保持源节点之间的连通性。当$s$较小时，这种现象尤为显著，从而解释了在较小的$s$值下网络寿命下降更陡峭的原因。

接下来，我们评估定理2.2和定理2.3中提出的稀疏矩阵（即公式(4)和(6)中的矩阵）的性能。图11和图12分别显示了最小剩余能量和网络寿命。对于方程(4)中的矩阵，我们设置$h= 1/\sqrt{n}, k=\log n, s= 1/\sqrt{n}$和$m=k^2 \log n=\log^3 n$。对于方程(6)中的矩阵，我们设置$k=\log n, s= 1/\log n$和$m=k\log n=\log^2 n$。我们观察到，在相同方案下，随着$n$的增加，最小剩余能量和网络寿命均呈下降趋势。这是因为每轮的平均源节点数在定理2.2中为$sn= O(\sqrt{n})$，在定理2.3中为$sn= O(n/\log n)$，两者都随$n$增加而增加。此外，$m$也随$n$增加。我们观察到，AM-REST对感知矩阵的最小剩余能量分别提高了24–78%和8–31%公式(4)和(6)中的感知矩阵分别使网络寿命提升了216–255%和105–122%。

最后，我们在不同的网络拓扑结构下评估所提出的算法的性能；具体而言，与之前的设置相比，采用了更为稀疏的网络。我们将通信范围$R$缩小至0.15。在这种情况下，当$n= 100$时，网络处于临界连通状态；因此，网络拓扑结构形成一个稀疏图。在接下来的仿真中，我们设置数据向量的稀疏性$k= \sqrt{n}$，并将每个传感器的初始能量设为1,000焦耳。图13比较了$R= 0.15$和$R= 0.5$、保留概率$s= 0.5$时的性能。我们观察到，在更稀疏的网络中性能更差：如果网络仅勉强连通，则许多非源节点必须参与聚合以维持网络连通性。相比之下，如果网络非常稠密，则聚合树可能仅由源节点构成，因此聚合所需的节点数量相对较少。图14比较了$n= 100$时，$R= 0.15$和$R= 0.5$在不同保留概率$s$取值下的性能。我们观察到性能趋势与图13相似。此外，对于较大的$R$，最小剩余能量随$s$的下降速度更慢。这是因为如果网络处于临界连通状态，可能存在一些节点无论$s$取何值都必须被包含在树中，以维持网络连通性网络连通性。因此，我们得出结论：直接影响能耗性能的树的大小对$s$相对不敏感。

7 实验

7.1 设置

在本节中，我们展示了所提出算法的实验结果。物联网实验室平台（IoT-LAB）是无线传感器网络和物联网最大的公共测试平台之一（Adjih 等人 2015）。它提供了大规模的开源实验平台，用于传感、计算和通信，使研究人员能够直接进行设计和监控，而无需构建单独的平台，这通常是一项复杂且耗时的任务。该平台提供命令行或基于Web的接口，用户可以在六个站点上启动实验，其中可访问2728个无线传感器。用户可以收集温度、大气压力、光照度和地震数据等传感器读数。该测试平台还提供工具，用于监测传感器节点的功耗、电流、电压消耗和接收信号强度指示。

我们在物联网实验室平台上进行的实验设置如下。对于硬件平台，我们选择了WSN430开放节点，由物联网实验室提供，该节点采用16位 MSP430F1611微控制器，配备10kB内存（Texas_ Instruments 2009）。该节点配备了TI CC2420芯片组（Texas_ Instruments 2006），用于无线通信，这是一种符合IEEE 802.15.4物理层标准的低功耗2.4GHz收发器。图15是WSN430开放节点的照片。图16显示了物联网实验室中传感器三维布局的一个示例。我们考虑一个维度为$4\times12$的网格拓扑结构，如图17所示；因此，共有48个节点。两个节点之间的间距为0.60米。

我们在Contiki上实现了测试程序，Contiki是一种轻量级开源操作系统，主要为物联网设备设计（Dunkels 等 2004）。对于MAC协议，Contiki操作系统使用了X-MAC的兼容版本（Buettner 等 2006），这是一种运行在802.15.4 物理层之上的异步占空比媒体访问控制协议。我们测试平台中分组通信的协议栈是Rime（Dunkels 2007），它是一种具有“精简”协议层的简化通信栈，适用于传感器网络。表2总结了我们的测试平台环境。

参数	值
微控制器	MSP430F1611
射频芯片	TI CC2420
PHY	IEEE 802.15.4@2.4 GHz
发射功率	0 dBm
OS	Contiki
MAC	X-MAC
协议栈	Rime
拓扑结构	$4\times12$ regular grid
节点间距	0.60米

与其他聚合方法（如CDG）类似，AMREST中的分组大小是固定的。在我们的实验中，节点生成并传输长度为8字节的假设感知数据，并通过AMREST构建的路由树进行聚合。随机感知矩阵$A$按照第3节所述的方法，使用PRNG以分布式方式生成。对于数据包传输，我们利用Rime协议栈提供的可靠单播机制。这是因为每个数据包最终都必须被传送到汇聚节点。因此，在实验中可能会发生偶尔的数据包重传。稍后，我们将进一步详细讨论此类重传问题。

接下来，我们将解释如何根据测量值计算节点的能耗。在实时测量功耗和剩余电池电量时存在两个问题。首先，WSN430节点在运行时无法直接获得能量消耗的实时测量值；相反，功耗可以从服务器上的日志文件中通过SSH接口读取。其次，WSN430节点工作在直流电源模式下，因此读取剩余电池电量是没有意义的。我们针对这些问题的解决方案如下：每个节点维护一个变量 residual_level ，用于表示该节点的假设剩余电池电量。在每次传输尝试时， residual_level 会减去变量 energy_per_tx ，该变量表示每次传输的能量消耗。 energy_per_tx 的值基于以下测量结果确定。

图18显示了一个节点的功耗测量结果。该图展示了WSN430发射器每隔3.5秒向接收器进行周期性数据包传输时的功耗情况。为了简化我们的功耗计算，仅将传输时刻（如图18中标记的峰值）的功耗计为实际的发送(TX)和接收(RX)功耗支出。3在每次传输时，我们从发送功耗的经验分布中随机生成 energy_per_tx 。该分布是根据如图18中的测量值得到的。类似地，对于接收功耗的估计也采用相同的步骤（例如，通过定义变量 energy_per_rx ）。

我们观察到，在图18中，接收功耗与发送功耗相似。这一观察结果与我们的假设一致，即发送和接收功耗大致相等，从而证明了我们假设的实用性。这也符合TI CC2420的技术规格，其中主动接收消耗电流为18.8mA，而主动发送消耗电流为17.4mA（Texas_ Instruments 2006年）。需要注意的是，为了实现AMREST，我们需要为节点$u$和$v$分配边权重$w(u,v)$，以表示每次数据包传输的能量消耗。我们将简单地将权重$w(u,v)$设置为节点$u$和$v$的每次发送能耗 energy_per_tx 与每次接收能耗 energy_per_rx 的平均值。

7.2 结果

在我们的$4\times12$图17所示的网格网络中，汇聚节点位于右上角。我们将稀疏参数设置为$k= \sqrt{n}$，使得所需的测量值数量为$m= \sqrt{n}\log n$，其中$n= 48$为本实验中的取值。传感器的初始能量水平设为0.35焦耳。在AMREST中，节点需要跟踪其他节点的能量水平。然而在实际中，可能会发生意外的能量消耗（例如数据包重传），这会导致节点的实际能量水平与其他节点对该节点能量水平的估计值之间出现偏差，而AMREST正是基于这些对能量状态的估计来运行的。因此，节点有必要偶尔向网络更新其剩余能量信息。为了防止节点发送过多的更新信息，我们将采用以下方法进行更新。

仅当节点的实际能量水平与其他节点的估计值存在显著偏差时，该节点才会向网络通知其能量水平。具体而言，仅在以下两种情况下节点才会发送更新：（i）当前能量水平与估计值之间的误差超过$\tau_1 \%$，且（ii）自上次更新以来的轮数超过阈值$\tau_2$。注意，条件（i）中的误差是相对于当前能量水平的。

其思想是，由于（i），能量水平较高的节点对少量重传相对不敏感；同时，（ii）防止了能量水平较低的节点过于频繁地发送更新。因此，我们的更新方法能够适应节点的剩余能量水平，而不会引起过高的通信开销。在我们的实验中，我们设置了$\tau_1= 5\%$和$\tau_2= 10$轮次。

图19显示了在情况$s= 0.2$下最小剩余能量的分布。我们得出了一些与仿真结果一致的观察结论。例如，AMREST下的能量水平 tends to be higher than those under the modified MST。此外，AMREST下能量水平的方差小于改进的MST下的方差。

接下来，我们研究AMREST对不精确的系统信息的鲁棒性。图20将实验结果与理想情况进行比较，我们定义的理想情况如下：假设在任何时候都可以无任何开销地获得整个网络节点的剩余能量水平的完美信息。相比之下，在实验中，AMREST可能由于例如意外的重传和其他节点能量消耗的随机性等原因而面临信息不精确的问题。精确的信息仅通过我们的更新方法间歇性地获得，而这会带来一定的通信开销。事实上，我们观察到性能在实验情况下的表现仅略逊于理想情况。然而，这种差距很小，因为我们的方法能够根据节点能量水平自适应地更新信息，而不会带来过多开销。这体现了我们算法的鲁棒性。

接下来，我们展示一些关于剩余能量信息更新的统计信息。信息更新主要由数据包重传引起。图21显示了网络中各轮次的数据重传次数。总体重传次数不高，这可能是由于实验中传感器之间的短距离和视距链路所致。图22显示了剩余能量信息发生更新的轮次。例如，当$s= 0.1$时，AMREST和改进的MST分别在第33轮和第22轮进行信息更新。总体而言，AMREST下的更新频率低于改进的MST，导致AMREST的开销更低。这是因为AMREST下的能量水平往往更高，而根据我们的更新方法，能量水平较高的节点更新其信息的频率较低。我们还观察到，当$s$取值较大时，更新变得更加频繁。这是因为网络中的源节点更多，导致能耗更高。

8 结论

在本研究中，我们提出了一种利用传感器节点稀疏随机采样的节能数据收集算法。我们的目标是在恢复原始数据向量时最大化最小剩余能量。我们提出了一种贪心算法，以逐轮方式优化数据收集过程。在每一轮中，我们根据固定概率随机选择源节点。我们证明了该问题是NP完全的，并提出了算法AMREST，用于近似构造每轮的最大最小剩余能量斯坦纳树。我们的分析表明，AMREST具有可证明的近最优性；在初始能量储备和边权重均匀的情况下，AMREST实现的最优性差距为常数，且不依赖于网络规模和拓扑结构。仿真结果表明，即使在感知矩阵为稠密的情形$s= 1$下，AMREST仍能延长网络寿命。此外，当$s<1$时，我们的方案在最小剩余能量和网络寿命方面均显著优于基线方案。