基于网络编码的WSN拓扑控制

基于网络编码的组播拓扑控制无线传感器网络

摘要

网络编码是一种有前景的技术，可提高吞吐量和可靠性。然而，网络编码的优势受到网络拓扑的限制并受其影响，尤其是在无线传感器网络（WSN）中尤为明显。拓扑控制算法通过调整传感器的传输参数，主要是传输功率，以实现期望的拓扑结构。因此，网络编码和拓扑控制算法均能降低功耗，延长无线传感器网络寿命。本文对基于网络编码的多播无线传感器网络中的最优拓扑控制进行了详细的数学建模，将其表述为一个混合整数非线性问题。尽管该问题是NP难的，但该数学建模有助于我们分析其本质并理解问题的复杂性。随后，我们提出了一种用于基于网络编码的多播无线传感器网络的启发式拓扑控制算法，该算法运行速度更快。通过在不同流量模式下的仿真结果验证了我们算法的有效性。我们得出结论：与传统算法相比，我们的算法可用于控制支持多播的无线传感器网络的拓扑，在显著提升生命周期方面表现更优。

关键词 ：WSNs；无线传感器网络；拓扑控制；生命周期；网络编码；组播。

1 引言

无线传感器网络（WSN）由大量不同类型的传感器组成，这些传感器通过无线介质连接以执行分布式感知任务。
在大多数无线传感器网络中，电源和通信带宽是受限的。由于能量有限且难以对大量传感器节点进行充电，因此能效和最大化网络寿命是传感器网络最重要的设计目标（Sohraby 等，2007）。
无线传感器网络通过大量传感器及其协调克服了资源限制。然而，大量传感器会导致冗余和资源利用不足问题，从而降低网络的有效吞吐量。换句话说，在密集部署的无线传感器网络中，单个传感器拥有许多邻近传感器，当使用足够大的传输功率时，可以直接通信。然而，这并不一定有益，因为（拉布拉多和怀特曼，2009；桑蒂，2005；罗伊和穆克吉，2012）：
- 高传输功率需要大量能量，导致无线传感器网络寿命缩短
- 许多邻居对MAC协议来说是一种负担
- 路由协议在网络中因传感器移动并频繁形成或断开许多链路而遭受不稳定性的影响。

如果传感器降低其传输功率，可能会对其他特性产生影响，例如延迟、冗余、感知覆盖和网络连通性。拓扑控制是一种帮助研究人员在无线传感器网络中优化这一权衡的方法。尽管使用拓扑控制带来的节能优势已被广泛认可，但拓扑控制是一个复杂的过程，若执行不当，可能产生不良结果。拓扑控制算法的主要目标是在保持网络与感知连通性和覆盖范围等重要特性的前提下延长无线传感器网络寿命（拉布拉多和怀特曼，2009；桑蒂，2005；罗伊和穆克吉，2012）。

另一方面，研究表明，通过利用无线信道的广播特性，网络编码在无线传感器网络容量方面可带来显著改进，并且与传统的非网络编码传输相比，能够降低多播流量的功耗（张等，2012）。大量研究已在网络编码的各个方面展开，例如编码方法（何和伦，2008）、网络编码的实际应用（巴茨等，2010）、面向能效的网络编码（普拉茨等，2008）等。已知网络编码可以有效提高吞吐量（明勋和永勇，2011），以及减少端到端延迟（显忠和爱娇，2011）。尽管已证明网络编码在无线传感器网络中具有诸多优势，但网络编码的性能依赖于网络拓扑（Kaikai，2008；利马等，2011；米什拉等，2010）。

鉴于未来网络编码可部署于无线传感器网络中，我们探讨了如何在网络编码型无线传感器网络中利用拓扑控制。
本文中，我们对基于网络编码的多播无线传感器网络中的拓扑控制进行了建模，并提出了一种考虑网络编码技术的无线传感器网络拓扑控制启发式算法。该算法试图充分利用网络编码的特性来节省带宽，同时延长无线传感器网络寿命。当然，所提出算法的复杂度较低，可以快速运行。

考虑图1所示的场景，其中传感器A、B和C共享公共无线介质。传感器A和C需要交换信息。由于信道约束，任何时刻只有一个传感器可以传输。实现此信息交换的可能方式如下。
- 传感器A具有高传输功率，并与C有直连链路，可将其数据包发送给C，反之亦然。如果应用了网络编码，该解决方案不会改变。
- 传感器具有较低的传输功率，A、C需要将它们的信息传输给B，然后B中继这些信息。这种方法需要四次传输，但传输功率较低。
- 网络编码被应用于减少传输次数。A和C依次向中心传感器B发送数据包。B节点不直接将每个数据包转发至其目的地，而是将两个数据包进行异或运算，并在共享介质中广播结果作为单个数据包。节点A和C均知道自身发出的数据包。整个过程恰好需要三次传输。

为简化起见，假设无线电信号根据自由空间模型传播，且我们仅关注最小化发射功率，路径损耗指数等于2。在此假设下，直接从A到C和C到A发送消息所需的功率与 $2(2r)^2=8r^2$ 成正比，其中r为传感器之间的距离；若数据包通过B中继，则总功耗与 $4r^2$ 成正比。如果应用网络编码技术，总功耗则与 $3r^2$ 成正比。显然，若同时应用拓扑控制算法和网络编码技术，第三种方案效果更优。

尽管在我们关注最大化寿命时，每个传感器的初始能量会影响最佳方案的选择。例如，如果B的能量非常低，则第一种方案是最佳方案。当然，关于无线传感器网络寿命有多种定义，将在后面进行解释。

上述观察结果为基于网络编码的多播无线传感器网络中的拓扑控制问题提供了第一个支持论据。
基于网络编码的多播无线传感器网络中的拓扑控制问题建立在传感器具备编码能力的假设之上，而将我们的问题与传统方法区分开的是应用于支持多播传输的网络编码技术。本文的主要贡献总结如下：
- 首次，我们对基于网络编码的多播无线传感器网络中的最优拓扑控制进行了详细的分析评估，将其建模为一个混合整数非线性规划（MINLP）问题。该数学建模有助于我们深入评估其本质，并更好地理解该问题的复杂性。
- 我们证明，通过采用网络编码技术来支持无线传感器网络中的多播传输，与传统的面向单播和基于Steiner树的设计相比，可以获得网络能耗显著降低且生命周期更长的多播网络拓扑。
- 我们提出了一种名为RANC（基于网络编码的无线传感器网络中的范围分配）的启发式算法，该算法能够更快速地控制无线传感器网络的拓扑，以实现基于网络编码的多播无线传感器网络中的高效拓扑控制。

本文其余部分组织如下：第2节介绍拓扑控制和网络编码的相关工作，第3节描述问题描述以及我们问题的建模。第4节提出我们的启发式算法，我们在第5节通过仿真评估我们算法的有效性，然后在第6节对本文进行总结。

2 相关工作

由Ahlswede等人（2000）提出的网络编码技术，在建立组播连接方面展现出巨大潜力，其带宽需求显著低于传统的基于Steiner树的多播连接。基于网络编码已有的鼓舞人心的研究成果，该技术成为分组网络中一种极具前景的实用技术。通过利用无线信道的广播特性，与传统非网络编码传输相比，网络编码能够显著提高网络吞吐量（何和伦，2008；Kaikai，2008）。

李等人（2003）表明，线性码足以实现多播流量的最大容量上限。科特和梅达尔德（2003）提出了用于编码和解码的多项式时间算法，而何等人（2004）将这些结果扩展到随机码。

卡蒂等人提出COPE，这是一种用于使用网络编码的无线网络的新架构。他们的结果表明，在转发层使用COPE而不修改路由和高层的情况下，可以提高网络吞吐量（卡蒂等人，2008）。

基于网络编码的多播连接的建立可以分解为两个阶段（Kaikai，2008；何和伦，2008）：
- routing：确定将使用哪些链路以及多少带宽资源
- coding solution construction：定义每个节点在选定的多播路由上的操作函数。

池等人（2010）研究了基于网络编码的多播网络的拓扑设计问题。基于多播和网络编码的特性，他们对问题进行了建模，并提出了两种启发式算法。他们通过仿真验证了所提启发式算法的有效性。其目标是最小化网络成本。

米斯拉等人（2010）建立了一个分析框架，用于在传输范围约束下预测编码性能。乔卡等人（2007）探讨了网络编码范式在拓扑推断中的应用。萨塔里等人结合网络编码和断层扫描技术进行拓扑推断。他们的目标是通过发送探测包以及执行网络编码操作来推断网络的拓扑结构（萨塔里等人，2009）。

沙阿‐曼苏里和黄（2010）将最大寿命最小资源编码问题表述为一个线性规划问题。他们的问题目标是联合最大化网络寿命并最小化执行网络编码的速率。

另一方面，已有许多关于拓扑控制的研究，并提出了多种机制。

由研究人员研究。拓扑控制机制主要选择合适的传输范围。Kirousis 等人（2000年）研究了拓扑控制以及如何为每个无线节点选择适当的传输功率；他们将其简化为传输范围分配问题，并讨论了其计算复杂性。

根据 Kirousis 等人（2000年）的研究，一维传输范围分配可以通过多项式时间求解，而二维和三维的传输范围分配问题是 NP难 的。

Marina 等人（2010年）研究了多无线电无线网状网络中的信道分配问题。他们提出了基于拓扑控制视角的信道分配图论建模，并证明了由此产生的优化问题属于NP完全问题。

Liu 等人提出了一种基于机会的拓扑控制。他们证明了基于机会的拓扑控制是一个NP难问题，并基于可靠性理论设计了一种完全分布式算法（Liu 等人，2010年）。

尽管存在许多拓扑控制机制，但这些机制尚未与网络编码相结合。然而，已有一些研究探讨了在网络编码中使用分层拓扑控制机制。Hui 等人（2009年）将网络编码应用于无线骨干网，并从理论视角分析了该方法的性能。他们的数值结果表明，编码机会概率随输出队列大小的增加而增加，随邻居数量的减少而增加。换句话说，网络编码在高流量负载和较少邻居的情况下更具优势。Hui 等人（2010年）随后提出了一种结合网络编码的骨干路由，其中骨干节点具有较少的邻居。所提出的结合网络编码的骨干路由实现了良好的吞吐量增益，尤其是在承载负载较高时。

Xiong 等人（2007年）专注于簇内信息交换。他们表明，无线网络的总能量消耗取决于总传输次数，而采用网络编码可以减少总传输次数。Munari 等人（2008年）分析了协作网络编码协议在簇内数据交换中的性能。他们提出了 Phoenix，这是一种随机接入协议，需要略微调整重传阶段以利用网络编码。Phoenix 特别适用于具有严格延迟要求的高密度网络。Wang 等人（2009年）比较了洪泛、中继和基于网络编码的信息交换。他们的仿真结果表明，网络编码始终比其他方法表现更好，尤其是当节点数量较大时。他们的仿真结果显示，网络编码可以大幅降低簇头的能量消耗。

网络编码技术和拓扑控制算法都能增强网络能力，然而，据作者所知，在现有的拓扑控制文献中，几乎所有的拓扑控制算法都忽略了网络编码。换句话说，目前尚无文献研究在考虑网络编码的情况下对网络拓扑进行控制的问题。

高效支持基于网络编码的多播无线传感器网络是当前的一个重要问题。

3 问题陈述与建模

在本节中，我们提出并形式化了问题描述。首先，我们介绍系统模型和定义，然后详细讨论该问题的不同方面，最后在数学上形式化基于网络编码的多播无线传感器网络中的拓扑控制问题。

3.1 系统模型和定义

在本文中，我们使用图模型，尽管完全规则的无线电覆盖假设是图模型的主要弱点。在现实情况下，由于墙壁、建筑物、与现有基础设施的干扰等因素的影响，无线电覆盖区域很可能是高度不规则的。然而，在网络模型中包含所有这些细节会使模型变得极为复杂且依赖于场景。因此，尽管存在局限性，图模型仍在无线传感器网络特性的研究中被广泛使用（Sohraby 等，2007； Shah‐Mansouri 和 Wong，2010）。

我们将无线传感器网络表示为一个超图，该模型能够有效描述无线链路的广播特性。设 $G =(V, A)$ 表示一个有向超图，其中 $V$ 是传感器集合，$A$ 是超弧集合。我们假设 $G$ 是有限的，即 $|A| < \infty$ （因此 $|V| < \infty$）。

设 $N_i$ 表示传感器 $i \in V$ 的邻居集合。超弧是一对 $(i, J_i)$，表示从传感器 $i$ 到邻近传感器子集 $J_i \subseteq N_i$ 的广播链路。网络中的超弧集合可以表示为
$$
A = {(i, J_i) | i \in V, J_i \subseteq N_i}
$$
我们用 $i$ 的传输范围表示为 $r_i$，显然 $\forall j \in J_i: d(i, j) \le r_i$ ，其中 $d(i, j)$ 是节点 $i$ 和节点 $j$ 之间的距离。

本文中使用的其他符号在表1中定义。

定义	符号
超弧 $(i, J_i)$ 的基数	$|J_i|$
传感器 $i$ 的入射超弧集合	In($i$)
传感器 $i$ 的出超弧集合	Out($i$)
传感器的容量（速率约束）	$C_i$
超弧 $(i, J_i)$ 中单播流的总速率	$f_{i}(J_i)$
网络中的组播源节点集合	$S$
源 $s_t \in S$ 发送数据的汇聚节点集合	组播数据 $D_{s_t}$
源 $s_t$ 从节点 $i$ 出发的组播流速率通过超弧 $(i, J_i)$	$g_{s_t}(J_i)$
所有会话在超弧上的实际发送速率 $(i, J_i)$ 在节点 $i$ 执行编码后	$Z(J_i)$
源目节点对之间的平均距离	$L$
节点 $i$ 生成的单播流	$G_f^u$
节点处的流目的地	$D_f^u$
由节点 $i$ 生成的组播流	$G_f^M$
节点处的流目的地 $i$	$D_f^M$

3.2 问题描述

在本小节中，我们将基于网络编码的多播无线传感器网络中的拓扑控制问题建模为混合整数非线性规划。我们问题的不同方面如下所示。

3.2.1 链路利用率约束

尽管每个传感器的最大传输容量已指定，但无线传感器网络中节点的可实现容量取决于网络规模、流量模式和详细的局部无线电交互。古普塔和库马尔（2000）估算了每节点容量的预期值。他们证明，在无线网络的总面积上，能够同时进行单跳传输的数据总量呈线性增长。他们还表明，随着节点数量的增加，每个节点可用的吞吐量趋近于零。

然后，在使用公共传输功率的情况下，$A$ 平方米网络的平均最大流量承载容量受到古普塔和库马尔（2000）的限制
$$
RC(i, J_i) = \frac{C_i}{16\pi L |J_i| \log |J_i|}
\quad \forall i \in V
$$

3.2.2 流量守恒约束

流量守恒定律指出，在communication网络中的每个节点，总流入流加上该节点的源发流，减去该节点的需求，等于总流出流。不同类型的流量守恒在下文中有说明（福特和富尔克森，2010）。

(A) 单播
尽管存在不同的单播路由算法，但必须对它们应用单播流守恒约束（福特和富尔克森，2010）。
$$
\sum_{x \in V, (x,i) \in \text{In}(i)} f_u(x, J_x) - \sum_{x \in \text{Out}(i)} f_u(i, J_i) = G_f^u - D_f^u \quad \forall i \in V
$$
$$
0 \le f_i(J_i) \le C_i
$$
方程(3a)中的第一项表示节点的总单播流入量，第二项表示节点的总单播流出量。

单播流还必须满足下界和容量约束(3b)，我们将其称为单播流边界约束。

(B) 基于Steiner树的组播
基于Steiner树的多播是x个单播的一种特殊组合。每个单播流均满足流量守恒约束（Shah‐Mansouri 和 Wong，2010；Chi 等，2010）。

到达节点 $i \in V$ 的组播流之和为
$$
\sum_{s_t \in S, x \in V, (x,i) \in \text{In}(i)} g_{s_t}(J_x)
$$
组播流之和从节点 $i \in V$ 流出 is
$$
\sum_{s_t \in S, (i,i) \in \text{Out}(i)} g_{s_t}(J_i)
$$
节点 $i \in V$ 中的流量守恒约束 equal to
$$
\sum_{s_t \in S, x \in V, (x,i) \in \text{In}(i)} g_{s_t}(J_x) + G_f^{M_i} - \sum_{s_t \in S, (i,i) \in \text{Out}(i)} g_{s_t}(J_i) = D_f^{M_i} \quad \forall i \in V
$$
$$
0 \le g_{s_t}(J_i) \le C_i
$$
组播流还必须满足下界和容量约束(4d)。

(C) 基于网络编码的组播
对于组播连接，采用基于网络编码的路由而非基于 Steiner树的路由的目的是实现用户最优路由，这可以显著减少每个连接的带宽消耗，从而降低网络中的总体资源消耗（Kaikai，2008）。

然而，基于网络编码的组播的流量守恒定律被表述为
$$
\sum_{s_t \in S, x \in V, (x,i) \in \text{In}(i)} g_{s_t}(J_x) + G_f^{M_i} - \sum_{s_t \in S, (i,i) \in \text{Out}(i)} g_{s_t}(J_i) = D_f^{M_i} \quad \forall i \in V
$$
$$
0 \le g_{s_t}(J_i) \le C_i
$$
显然，这些公式与方程(4(c)和(d))相同；我们在第3.2.4 节中展示了基于网络编码的组播与基于Steiner树的组播之间的差异。

3.2.3 网络可靠性要求

无线传感器网络节点和链路的故障原因有很多。在拓扑结构设计中必须考虑网络可靠性（Sohraby 等，2007）。

衡量网络可靠性的方法有多种。此处及其他一些文献中，使用k连通性概念作为可靠性度量。图 G被称为k连通的，其中 $1 \le k < n$，如果对于任意一对节点i、j ，至少存在k条节点不相交路径连接它们。1‐连通 图也称为简单连通。当网络是k连通时，最多可容忍k – 1个节点或链路故障而不导致网络断开。因此，k连通网络比简单连通网络具有更强的容错能力（Chi 等，2010； 桑蒂，2005；苏尔霍内等，2010）。

满足k连通性的无线传感器网络通常相比简单连通的无线传感器网络也能实现更好的负载均衡。而更好的负载均衡意味着网络中的能耗分布更加均匀，这可能会延长无线传感器网络寿命（桑蒂，2005；苏尔霍内等，2010）。

定理 1 （Bettstetter, 2002） ：在一个具有n个均匀分布的节点的无线多跳网络中（n >> 1），如果图中的最小节点度至少为k，其中{k 1 ≤ k < n}，则该网络至少是k连通的。

3.2.4 基于网络编码的组播

尽管在传统路由中获取组播连接是一个斯坦纳问题，属于NP难问题。利用网络编码的流共享特性和无线信道的广播特性，每条超弧上的实际流速率只需取各链路流的最大值即可。无线传感器网络中构建组播拓扑的问题可表述如下（何和伦，2008；Li 等，2003； Shah‐Mansouri 和 Wong，2010；Kaikai，2008）：
$$
\text{minimise: } \sum_{(i, J_i) \in A} a_{(i, J_i)} Z_{(i, J_i)}
$$
主题为：
$$
\sum_{s_t \in S, x \in V, (x,i) \in \text{In}(i)} g_{s_t}(J_x) + G_f^{M_i} - \sum_{s_t \in S, (i,i) \in \text{Out}(i)} g_{s_t}(J_i) = D_f^{M_i} \quad \forall i \in V
$$
然后对于所有$(i, J_i) \in A$，我们有
$$
0 \le Z_{(i, J_i)} \le \max_{s_t \in S} g_{s_t}(J_i)
$$
$$
0 \le Z_{(i, J_i)} \le RC(i, J_i)
$$
这是一个具有多项式时间算法以获得最优解的线性规划问题。已证明 $Z_{(i, J_i)}$ 是该线性规划问题的最优解，当且仅当存在网络编码。在此公式中， $a_{(i, J_i)}$ 是放置在超弧上的单位速率所需支付的成本（例如，货币成本、能量成本或虚拟权重成本）（何和伦，2008；Li 等，2003； Shah‐Mansouri 和 Wong，2010；Kaikai，2008）。

设 $E_i$ 表示传感器 $i$ 的初始能量， $P_{(i, J_i)}$ 表示传输一比特数据所消耗的功率超弧$(i,J_i)$。这等于向集合 $J_i$ 中最远节点传输数据所消耗的功率。因此，$P_{(i, J_i)} = \max_{j \in J_i} P_{ij}$，其中 $P_{ij}$ 表示从节点 $i$ 到节点 $j$ 传输一比特数据所消耗的功率（ Shah‐Mansouri 和 Wong，2010；Sohraby 等，2007）。

我们假设活动传感器在感知时消耗的能耗可忽略不计。假设无线电信号按照自由空间模型传播，则从传感器 $i$ 直接发送数据到传感器 $j$ 所需的功率等于
$$
P_{ij} = \eta_1 + \eta_2 r_{ij}^\alpha
$$
其中 $\alpha$ 是路径损耗指数，$2 \le \alpha \le 6$ 取决于环境，$\eta_2$ 是阈值，$\eta_1$ 是发射机电路消耗的功率。

给定 $E_i$ 和 $P_{(i, J_i)}$，节点 $i$ 的生命周期可以表示为（ Shah‐Mansouri 和 Wong，2010；Sohraby 等，2007）：
$$
\Gamma_i(z) = \frac{E_i}{P_{(i, J_i)} Z_{(i, J_i)}} \quad \forall i \in V
$$
我们的目标是最大化 $\Gamma_i(z)$ 或最小化 $1/\Gamma_i(z)$，即：
$$
\frac{1}{\Gamma_i(z)} \propto \frac{r_i^\alpha Z_{(i, J_i)}}{E_i} \quad \forall i \in V
$$
我们把 $\frac{r_i^\alpha}{E_i}$ 视为 $a_{(i, J_i)}$，并为每个多播需求构造最大寿命多播连接。

但在基于Steiner树的多播情况下，每条超弧上的实际流速率需要是所有独立链路流的总和，即公式(6(c))变为（Chi 等，2010；Kaikai，2008；Shah‐Mansouri 和 Wong，2010）：
$$
Z_{(i, J_i)} \le \sum_{s_t \in S} g_{s_t}(J_i)
$$

3.2.5 延迟要求

必须将平均端到-end数据包延迟保持在可接受值范围内。

大多数文献中采用基于Kleinrock的独立性假设的 M/M/1排队模型来计算每个网络链路上的平均数据包延迟。

基于该模型，平均端到-end数据包延迟可以表示为（Chi 等，2010；Kaikai，2008）
$$
T = \sum_{i \in V} \frac{Z_{(i, J_i)}}{RC(i, J_i) - Z_{(i, J_i)}}
$$
其中 $\gamma$ 是网络中以每秒分组数为单位的总到达率。

3.3 公式化

现在，所考虑的拓扑控制问题可以表述如下。

给定：
1. 传感器数量 $N$ 和距离矩阵 $[d_{i,j}] {N\times N}$
2. 每个传感器的剩余能量 $[E_i]_N$
3. 每个传感器的最大可访问容量 $[C_i]_N$
4. 单播流量需求 $[D_f^u]_N$ 和 $[G_f^u]_N$
5. 多播节点集 ${s_t, dt_1,…, d {tx}}$ 和流量速率 $[D_f^M] N$ 和 $[G_f^M]_N$
6. 连通性 $k$
7. 最大传输范围 $R {\text{max}}$
8. 最大容忍延迟 $T_{\text{Max}}$

最小化
$$
\sum_{i \in V} \frac{r_i^\alpha Z_{(i, J_i)}}{E_i}
$$
在设计变量上
$r_i, Z_{(i, J_i)}, f_{(i, J_i)}, g_{(i, J_i)}$

约束条件
(1) 网络可靠性要求：每个传感器至少具有 $k$ 个传感器不相交。
$$
|J_i| \ge k
$$
(2.1) 单播流守恒约束
$$
\sum_{x \in V, (x,i) \in \text{In}(i)} f_u(x, J_x) - \sum_{x \in \text{Out}(i)} f_u(i, J_i) = G_f^u - D_f^u \quad \forall i \in V
$$
(2.2) 基于网络编码的组播流守恒约束
$$
\sum_{s_t \in S, x \in V, (x,i) \in \text{In}(i)} g_{s_t}(J_x) + G_f^{M_i} - \sum_{s_t \in S, (i,i) \in \text{Out}(i)} g_{s_t}(J_i) = D_f^{M_i} \quad \forall i \in V
$$
And
$$
0 \le g_{(i, J_i)}, f_{(i, J_i)} \le C_i
$$
(3) 延迟要求
$$
T \le T_{\text{Max}}
$$
(4) 最大传输范围
$$
r_i \le R_{\text{max}}
$$
(5) 基于网络编码的组播连接
$$
Z_{(i, J_i)} \le \max_{s_t \in S} g_{s_t}(J_i)
$$
$$
0 \le Z_{(i, J_i)} \le f_{(i, J_i)} + RC(i, J_i)
$$
$$
RC(i, J_i) = \frac{C_i}{16\pi L |J_i| \log |J_i|}
$$
(6) 连通性
$$
\forall j \in J_i: d(i, j) \le r_i
$$
变量 $RC_{(i, J_i)}$ 是用于简化符号和公式的辅助变量。

通过该公式构建的编码子图问题的可行集即为最大生命周期基于网络编码的多播拓扑控制问题。这是一个 MINLP问题。MINLP模型是结合了组合性与非线性的模型。MINLP模型比混合整数线性规划(MIP)和非线性规划(NLP)模型都要困难得多。目前存在多种MINLP求解器，这些求解器在所采用的方法上有所不同。

最后，很明显，与传统拓扑控制问题相比，该问题具有额外的约束，例如网络编码传输的流守恒约束。

定理2 ：基于网络编码的多播无线传感器网络中的拓扑控制是NP难的。

证明 ：我们可以通过两种方法来证明这个定理：
1. 这个问题是二维或三维中的范围分配，因此根据（Kirousis等人，2000），它是NP难的
2. 因为它是一个MINLP问题，所以是NP难的（ Kaikai，2008；何和伦，2008）。

对于NP难优化问题，不存在用于获得最优解的多项式时间算法，求解该问题需要更长的时间。另一方面，拓扑控制算法必须多次运行，因此有必要开发启发式算法来应对。但数学建模有助于我们评估问题的本质，理解问题的复杂性，并作为与其他启发式算法进行评估和比较的标准。

4 拓扑控制的启发式算法

在本节中，我们将介绍一种名为RANC的启发式算法。
该算法的目标是控制一种基于网络编码的组播拓扑，以最大化无线传感器网络寿命。

RANC 是一种范围分配函数，它为每个 $i \in V$ 分配一个传输范围 $r_i$，其中 $0< r_i \le R_{\text{max}}$。

通常，我们希望找到图 $G$ 的一个子图 $G’$，该子图具有低传输范围，并且比原始图稀疏得多。

使用 $G’$ 而不是 $G$ 的优点在于（苏尔霍内等，2010；桑蒂，2005）。
- 如果 $G’$ 比 $G$ 稀疏得多，则路由开销会降低
- 许多邻居节点不会给MAC层带来负担。因此，它提高了空间复用，缓解了MAC层介质竞争，并减少了干扰
- 使用较低的传输范围可以延长无线传感器网络寿命
- 降低传输功率可以消除暴露终端问题。

RANC算法从传感器的最大传输范围开始，通过减小传输范围来删除一些链路，直到无法进一步减少为止，从而生成一个能耗相对较低的拓扑。

在RANC算法中，所有传感器以最大传输范围进行传输，并将其记为G。然后通过选择一个传感器并减小其传输范围，得到一个临时配置G′。如果G′满足某些特定条件，则意味着基于G′可以获得一个能耗更低的可行拓扑。将这个新的可行拓扑接受为G，并丢弃旧的拓扑。如果G′不满足所有这些条件，则将其丢弃。再获取另一个G′并进行测试。这些条件与(12)中的条件相同。

通过这种方式，反复执行减小传输范围的操作，直到没有任何合适的传感器能够进一步减小其传输范围为止。

我们通过在每个节点 $m_i$ 上定义效率度量
$$
m_i = \frac{r_i^\alpha}{E_i} \times Z_{(i, J_i)}
$$
这决定了哪个传感器必须减小其传输范围。显然，$m_i$ 与 $\Gamma_i(z)$ 相关，且具有较低 $m_i$ 的传感器的生命周期也较短。

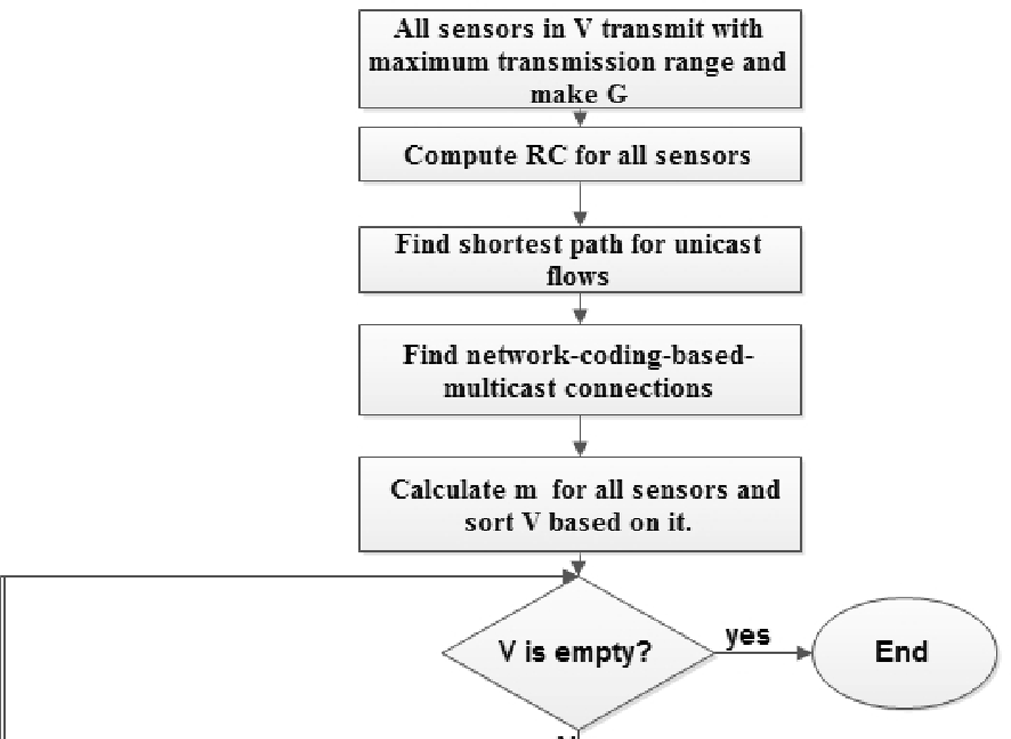
该算法的流程图如图2所示。

此过程包括以下详细步骤 s:
1. 索引 $N$ 个传感器，从 $1$ 到 $N$ 随机编号，所有传感器以最大传输功率进行传输（即，$\forall i \in V: r_i \leftarrow R_{\text{max}}$）。将得到的拓扑视为 G。
2. 根据公式(2)计算 $RC(i)$，当然 $|J_i|$ 是 $i$ 的邻居数量
3. 对于每个单播需求，选择源节点与目的节点之间的最短距离路径作为其路由。此步骤可通过多种算法（如 Dijkstra等）实现。
4. 对于每个多播需求，选择通过基于网络编码的组播问题获得的路由作为其路由。如果 $a_{(i, J_i)} = 1$（ Das 等，2004；Kaikai，2008；Li 等，2003； Shah‐Mansouri 和 Wong，2010），则可通过求解方程(6)优化问题来计算。
5. 计算每个传感器 $m_i$，其中包含候选传感器以降低其传输范围，并根据该值对 $V$ 进行排序。
6. 检查 $V$ 是否为空？若是，则转到步骤10。
7. 从 $V$ 中选择效率度量值较小的传感器 $i$。通过减小 $i$ 的传输范围获得一个临时配置（即，删除 $i$ 与其最远邻居之间的链路）。
8. 仅对那些在 $G’$ 中经过传感器 $i$ 的单播和多播需求重新分配路由。
9. 测试此临时配置是否满足以下约束。
$$
0 \le Z_{(i, J_i)} \le f_{(i, J_i)} + RC(i, J_i)
$$
$$
|J_i| \ge k
$$
$$
T \le T_{\text{Max}}
$$
如果这个新拓扑满足约束，且 $G’$ 的生命周期优于 $G$，则接受此临时拓扑作为 $G$，重新计算 $m_i$ 并重新排序 $V$。然后，返回步骤6。
如果不是，则丢弃该临时配置，并从候选集 $V$ 中移除传感器 $i$。然后，返回步骤6。
10. 退出并返回 $G$ 作为最终拓扑。

然而，这是一种贪心算法，通过选择寿命较短的传感器并减小其传输范围来尝试延长无线传感器网络寿命。这种减小会导致传感器的传输功率降低，经过该传感器的流量减少，从而增加传感器寿命。

5 性能评估

在本节中，我们评估了所提出的拓扑控制算法的性能。拓扑控制算法的性能可以通过与同一问题的现有优秀算法进行比较来评估，或者通过衡量该算法实现的无线传感器网络寿命与最优无线传感器网络寿命上界之间的差距来评估。

遗憾的是，目前尚无在考虑网络编码的无线传感器网络中使用拓扑控制的启发式算法，且仅对简单情况已知上界，更不用说基于网络编码的多播无线传感器网络中的拓扑控制了。

为了评估我们算法的性能，我们考虑一组20个传感器，其位置在尺度为30 × 30米的范围内随机选择。随机拓扑在无线传感器网络中已被广泛使用（Shah‐Mansouri 和 Wong，2010；Kaikai，2008）。传感器区域的四个角落设有四个汇聚节点。每个数据包的大小为256比特。最大传输范围为10米。路径损耗指数 $\alpha$ 设为3。我们选择 $\eta_1= 100$ pJ/s/m 和 $\eta_2= 1$ nJ/sec（Shah‐Mansouri 和 Wong，2010）。

每个传感器节点的初始能量根据700焦耳到1500焦耳之间的均匀分布随机生成。我们假设传感器节点是同步的，并且无线传感器网络必须至少是2‐连通的。传感器最大容量设置为10千比特每秒。

算法产生的拓扑寿命取决于输入参数值以及该算法的性能。工作负载（即来自所有传感器的总流量）是一个与拓扑寿命密切相关的重要的输入参数。

另一方面，生命周期的精确定义取决于具体的应用。一种简单的选择是将第一个传感器失效（或耗尽能量）的时间作为无线传感器网络寿命。其他选择包括一定比例的传感器耗尽能量的时间。前者过于悲观，因为当一个传感器失效时，其余传感器仍然可以提供适当的功能。

在我们的实验中，比较了不同工作负载下能量耗尽并关闭的传感器数量。

特别是，我们比较了以下三种情况生成的拓扑寿命。
- 一个混合整数问题，该问题在第3.3节中由(12)描述。我们称之为OTRA（最优传输范围分配），并使用 Bonmin（Lougee‐Heimer, 2003）来求解它。
- 我们提出的启发式算法（RANC），该算法在第4节中进行了描述。对RANC的分析是使用MATLAB和ILOG CPLEX优化库进行的。
- Das 等人 (2004) 提出的混合整数线性模型用于构建基于最大寿命Steiner树的多播。该问题通过Bonmin求解以获得全局最优解。我们将其称为No_Coding，并使用 Bonmin（Lougee‐Heimer, 2003）来求解。

Bonmin 是一个开源MINLP求解器和框架，实现了基于非线性规划的分支定界法（NLP‐BB）和外逼近法（OA）算法。

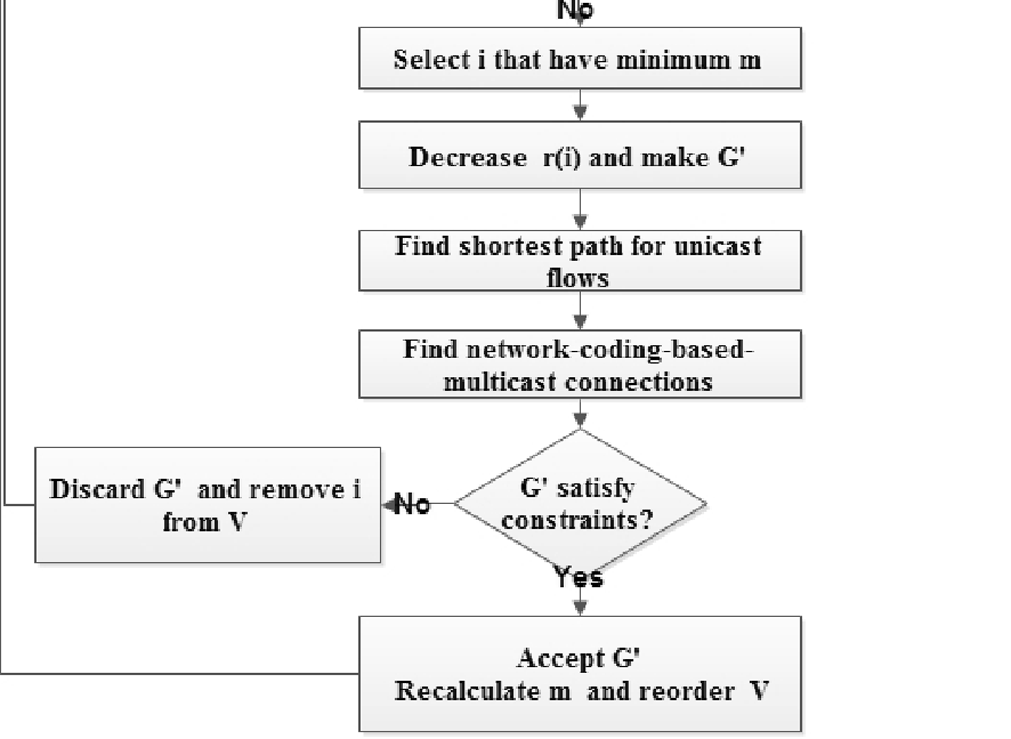
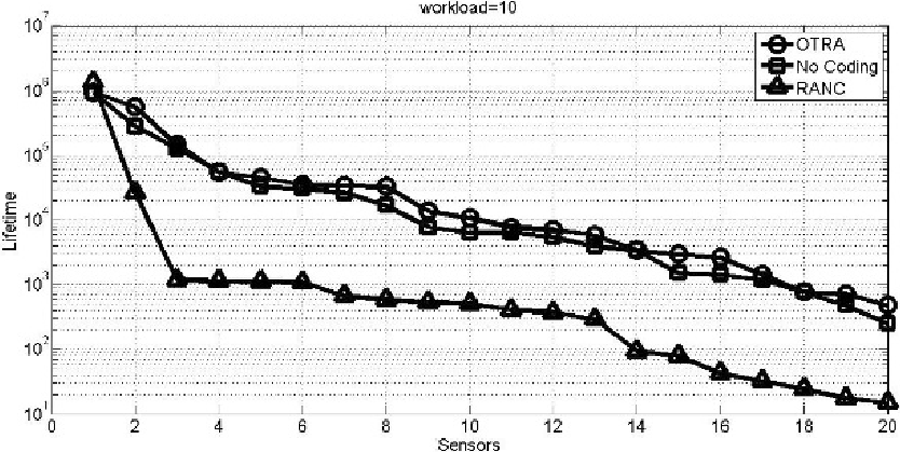
图3显示了在低工作负载（16个源节点每个产生10千比特每秒的流量，工作负载等于160 kbps）下传感器寿命随时间的变化。显然，OTRA和No_Coding生成的拓扑寿命高于RANC生成的拓扑寿命，且OTRA与No_Coding之间的差异较小。这是因为OTRA和No_Coding提出了最优解。换句话说，由于RANC不是最优解，因此从中获得的拓扑在相同低工作负载下的寿命低于OTRA和No_Coding所得的拓扑。当工作负载较低时，拓扑中的超弧通常承载较少的流量，因此编码机会也较低。因此，OTRA与No_Coding之间的差异较小。

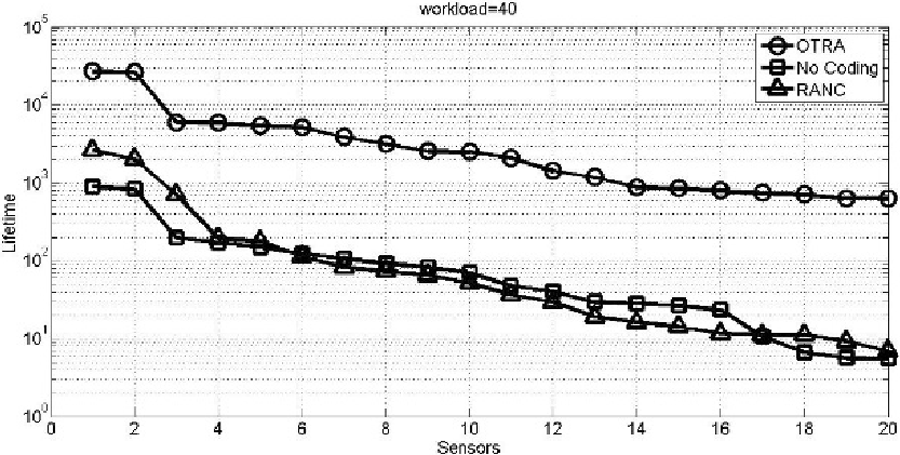
当工作负载从160 kbps增加到640 kbps时，No_Coding与OTRA之间的拓扑寿命差异增大。如图4所示， No_Coding的拓扑寿命小于OTRA生成的拓扑寿命。OTRA的拓扑寿命随着工作负载增加而增加的原因是，当工作负载增加时，每条超弧上的流量将增长，从而编码机会也会增加。另一方面，RANC生成的拓扑寿命增加，并在此工作负载下与No_Coding生成的拓扑寿命几乎相同。这是因为RANC利用了网络编码。

然而，当工作负载非常高（1120 kbps）时，得益于网络编码优势的OTRA和RANC比No_Coding具有更长的拓扑寿命。如图5所示，使用OTRA的无线传感器网络的生命周期明显长于RANC，而RANC又长于No_Coding。这是合理的，解释如下。传感器的能耗与传输次数成正比，而可能的网络编码机会数量通常随着传输次数的增加而增加。因此，OTRA生成的拓扑寿命相应增加。由于No_Coding不使用网络编码，其拓扑寿命小于RANC。

在下一个实验中，我们测量通过所有传感器的平均流量，即
$$
\text{Avg flows} = \frac{\sum_{i \in V} Z_{(i, J_i)} + \sum_{i \in V} f_{(i, J_i)}}{20}
$$

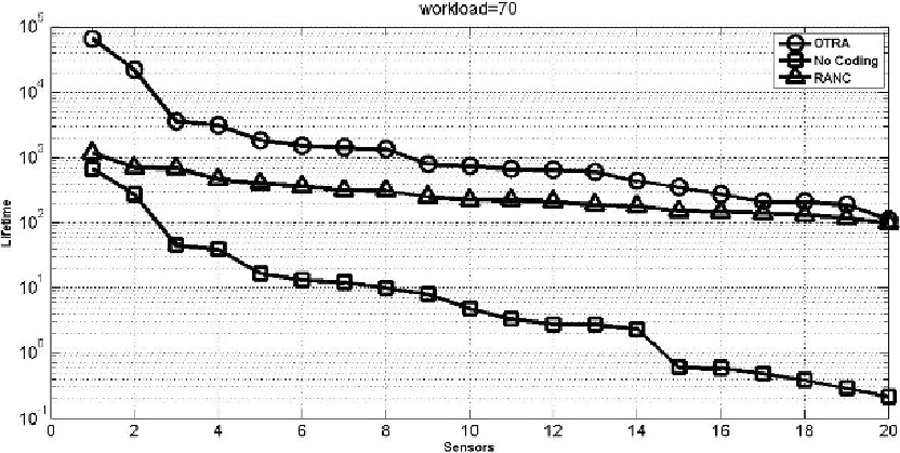
图6显示了不同工作负载下每个传感器的平均流量。显然，在低工作负载下，RANC中每个传感器的平均流量高于 No_Coding 和 No_coding，且相比OTRA更高。但在高工作负载下，RANC优于No_coding。

从这些结果可以看出，所提出的算法在高工作负载下优于No_coding，在中等工作负载下性能相当。但我们的一台配备Intel i5 2.53 GHz处理器和双核2GB内存的Windows 7电脑上运行了所有仿真。RANC仿真执行在每个工作负载下耗时两分钟，而求解OTRA和No_Coding问题的仿真运行大约需要一天时间。因此，我们的算法复杂度优于OTRA和No_coding。接下来，我们将计算我们算法的复杂度。

5.1 复杂度分析

单播需求的路由复杂度为 $O(N^2)$，因此 $u$ 个单播需求的复杂度为 $O(uN^2)$。存在 $M$ 个多播需求，对于每一个多播需求，采用简单方法来获得基于网络编码的组播。该简单方法的期望复杂度为 $O(cv)$，其中 $c$ 是约束方程的数量（对于基于网络编码的组播等于 $3 \times |S| \times N$），$v$ 是线性规划问题中的变量数量（等于 $(1+ |S|) \times N^2$）。因此，构建一个多播路由的期望复杂度为 $O(|S|^2N^3)$，其中 $S$ 为多播节点集。$M$ 个多播需求的路由所需时间为 $O(M|S|^2N^3)$。所有复杂度均在表2中描述。

Step	复杂度
单播需求的路由	$O(N^2)$
$u$ 单播需求	$O(uN^2)$
为 $M$ 个多播需求进行路由	$O(M|S|^2N^3)$
计算 $m_i$	$O(N)$
根据 $m_i$ 对 $V$ 进行排序	$O(N^2)$
检查算法需求	$O(N^2)$
为单播流寻找最短路径	$O(uN^2)$

while循环重复执行，直到 $V$ 为空，对每个传感器最多执行 $N$ 次传输范围缩减。因此while循环的最大重复次数等于 $N^2$ 次。因此最坏情况算法复杂度等于
$$
\sum_{i=1}^{N^2} \left( O(uN^2) + O(M|S|^2N^3) + O(N) + O(N^2) + O(uN^2) + O(M|S|^2N^3) + O(N^2) \right)
$$
因此，我们的算法可以在多项式时间内确定性地完成，最多需要 $O(M|S|^2N^5)$ 次迭代，其中 $N$ 是涉及的传感器数量，且远优于NP难的No_Coding和OTRA。

6 结论与未来工作

由于传感器能量是无线传感器网络中最宝贵的资源，因此如何有效利用能量以延长无线传感器网络寿命成为大多数无线传感器网络研究的焦点。拓扑控制和网络编码均能降低功耗并延长生命周期。我们研究了基于网络编码的多播无线传感器网络中用于延长生命周期的具有挑战性的拓扑控制问题，并根据多播和网络编码的特点将其建模为混合整数非线性规划。但该模型是NP难的，因此我们提出了一种启发式算法。通过仿真验证了所提出的启发式算法。结果表明，如果拓扑控制算法能够充分利用基于网络编码的组播特性，则较大的工作负载会带来拓扑寿命的增加。我们计算了所提算法的复杂度，结果显示其具有多项式复杂度，远优于NP难的解决方案。

遗憾的是，所提出的算法是集式的，不适用于传感器数量较多的无线传感器网络。尽管在分簇无线传感器网络中，簇头可以运行所提出的拓扑控制算法。作为我们未来工作的一部分，我们将增强该算法，使其成为适用于非理想通信信道的分布式算法。