锥形通道磁流变支座优化

流动模式下带锥形通道的磁流变支座的磁路设计与优化

1. 引言

众所周知，发动机悬置是一种非常重要的汽车部件，能够抑制车辆发动机振动向车架的传递，提高车辆的舒适性。因此，理想的悬置应在车辆受到冲击时具有高刚度和大阻尼力，而在高频时具有低刚度和小阻尼力（Chen 和 Dong，2014；Yu 等，2001）。根据隔振方式的不同，发动机悬置可分为被动悬置、主动悬置和半主动悬置：被动悬置结构简单、制造成本低，但在高频下其动态硬化现象严重，动态刚度显著增加（Santhosh 等，2020）；主动悬置依靠外部动力驱动，在宽带环境下具有良好的隔振性能，但其结构复杂、能耗高、成本高，限制了其在工业领域的广泛应用（Guo 等，2019）；半主动悬置采用磁流变液、电流变（ER）液体和磁流变弹性体，在磁场或电场中表现出可控的阻尼/刚度特性，可有效控制振动传递和位移（Ruan，2017；Wang，2017）。

根据工作模式，磁流变支座可分为流动模式、剪切模式和挤压模式（Phu 和 Choi，2015）。

目前，大多数流动模式磁流变支座具有径向或周向阻尼通道。Yoon 等人（2018）提出了一种带有径向阻尼通道的紧凑型磁流变支座，在电流为 0.5 A 时可产生 1500 N 的阻尼力。该磁流变支座能够满足重型车辆在恶劣环境条件下工作的需求。

阮等人（2013a）提出了一种高阻尼磁流变支座，该支座采用环形流动和径向流动的磁流变阀结构以产生高阻尼力。与传统支座相比，磁流变支座的屈服压力和阻尼力之比高于传统支座。

相同的阻尼力下，功耗更低；在相同的功耗下。

康等人（2013）研究了船用柴油机的可控磁流变支座。为了在有限空间内提高阻尼力，采用径向和环形结构的阀式磁流变支座来增加阻尼力。当电流为2 A时，可产生25千牛的阻尼力，且功耗小于30千瓦。

然而，当磁芯的内径过大时，磁流变液在径向或环形阻尼通道中的磁感应强度会过早饱和（Dai 等，2015）。

基于一些研究，本文提出了一种用于流动模式下锥形阻尼通道的新型磁流变支座。为了缓解磁路中磁通密度的饱和现象，分析了阻尼通道几何参数对磁通密度和压降的影响。随后，通过ISIGHT和ANSYS建立了协同仿真优化平台。优化结果表明，所设计的磁流变支座提高了阻尼通道磁通密度的饱和点，且产生的压降具有良好的可控性。

2. 几何与数学模型

锥形阻尼通道磁流变支座结构如图1所示。它主要由磁芯组件、阻尼通道、橡胶弹簧和底膜组成。此外，磁芯组件包括励磁线圈、内磁芯和外磁芯。它将振动隔离腔分隔为上腔和下腔，腔室内充满磁流变液。内磁芯与外磁芯之间的锥形阻尼通道

磁芯和外磁芯。线圈安装在内磁芯中，将磁通量传导至位于阻尼通道另一侧的外磁芯。当电流通过线圈时，磁力线穿过流道，激活磁流变液，使液体内的颗粒形成链状结构，阻碍两腔室之间的流动。

2.1. 压降模型

磁路设计是实现磁流变支座的关键技术之一。为了在制造前预测磁流变支座的性能，基于其物理结构建立了数学模型。如图2所示，磁路的阻尼通道是磁流变支座的核心，因为支座的振动隔离性能由阻尼通道的压降决定。然而，压降的变化受到磁通强度的影响，而磁通强度由磁路结构和电流密度决定。

磁流变液在流动模式下工作，因为内磁芯和外磁芯保持静止。当倾斜角u = 0°时，阻尼通道为径向流动结构。实际上，径向流动结构在展开后为平行板缝流。粘性压降表达式为（张，2002）：

$$
\Delta p_h(u=0^\circ) = \frac{12\eta qL}{2\pi R_1 H_0^3} \quad (1)
$$

其中，$R_1$ 为内磁芯的内径，$L$为磁芯的高度，$H_0$ 为阻尼通道的间隙宽度，$q$为阻尼通道中的流量，$\eta$为无外加磁场时的流体粘度。

屈服压降表示为（邓等，2020）：

$$
\Delta p_t(u=0^\circ) = \frac{2L_1}{H_0} \cdot \tau_y \quad (2)
$$

其中$L_1$为有效磁极长度，$L_1=L_2,$和$\tau_y$为剪切屈服应力。

径向流道的总压降为：

$$
\Delta p(u=0^\circ) = \Delta p_h(u=0^\circ) + \Delta p_t(u=0^\circ)
= \frac{12\eta qL}{2\pi R_1 H_0^3}
+ \frac{2L_1}{H_0} \cdot \tau_y \quad (3)
$$

当倾斜角 $u > 0^\circ$ 时，流道呈锥形。实际上，展开平行板的弧度定义为 $a$，如图3所示。锥形磁芯的倾斜角 $u$ 与弧度 $a$的关系如下：

$$
\Delta p_h = \frac{12\eta q}{2\pi \sin u H_0^3} \cdot \ln \frac{R_2}{R_1} \quad (4)
$$

整个平行板中的粘性压降表示为（张，2002）：

$$
\Delta p_h(u=2\pi) = \frac{12\eta q}{2\pi H_0^3} \cdot \ln \frac{R_2}{R_1} \quad (5)
$$

根据公式(4)和(5)，锥形阻尼通道的粘性压降可得如下：

$$
\Delta p_h(u>0^\circ) = \frac{12\eta q}{2\pi \sin u H_0^3} \cdot \ln \frac{R_2}{R_1} \quad (6)
$$

其中 $R_1$ 和 $R_2$ 是圆盘的内径和外径，分别对应内磁芯的下直径和上直径。

根据公式(2)，锥形阻尼通道的屈服压降为：

$$
\Delta p_t(u>0^\circ) = \frac{C\tau_y}{H_0} \left(L_1 + \frac{L_2}{\cos u}\right) \quad (7)
$$

其中：$C$ 为修正系数，取值范围为 2–3。当 $\Delta p_t(u>0^\circ)/\Delta p_h(u>0^\circ)<1$ 时，$C$ 等于 3；当 $\Delta p_t(u>0^\circ)/\Delta p_h(u>0^\circ)>100$ 时，$C$ 等于 2（阮等，2013b）。

因此，阻尼通道的总压降为：

$$
\Delta p(u>0^\circ) = \Delta p_h(u>0^\circ) + \Delta p_t(u>0^\circ)
= \frac{12\eta q}{2\pi \sin u H_0^3} \cdot \ln \frac{R_2}{R_1}
+ \frac{C\tau_y}{H_0} \left(L_1 + \frac{L_2}{\cos u}\right)
\quad (8)
$$

2.2. 磁感应时间常数

为了诱导磁流变液黏度的变化，需要产生磁通量，因此必须通过分析磁路来准确预测施加到磁流变液上的磁场，该磁路作为向磁流变液提供磁通量的‘供给线’。

如图4所示，根据磁路的等效原理（郑等，2016），磁阻$Q_1, Q_2, Q_3, Q_4$和$Q_0$分别对应于磁路的五个区域 A1、A2、A3、A4和A0。

每个磁阻根据磁路的欧姆定律分别计算（廖等，2012）。

$$
Q_1 = \frac{L - \frac{1}{2}(L_1 + L_2)}{\pi(R_2 - R_1)\mu_1} \quad (9)
$$

$$
Q_2 = \frac{R_2}{\pi R_2 L_1 \mu_1} \quad (10)
$$

$$
Q_3 = \frac{R_1}{\pi R_1 L_2 \mu_1} \quad (11)
$$

$$
Q_4 = \frac{L - \frac{1}{2}(L_1 + L_2)}{\pi(R_1 + L_2 \tan u)L_0 \mu_1} \quad (12)
$$

其中，$\mu_1$ 是内、外磁芯的相对磁导率。

根据阻尼通道内磁通密度的分布特性，有效磁阻尼通道由上部通道和下通道组成。因此，A0的等效磁阻表示为

$$
Q_0 = Q_{01} + Q_{02} \quad (13)
$$

其中，$Q_{01}$ 是上通道的磁阻，$Q_{02}$ 是下通道的磁阻。

$$
Q_{01} = \frac{H_0}{2\pi \mu_0 (R_2 - 0.5H_0 - 0.5L_1 \tan u)L_1} \quad (14)
$$

$$
Q_{02} = \frac{H_0}{2\pi \mu_0 (R_1 + 0.5H_0 + 0.5L_2 \tan u)L_2} \quad (15)
$$

其中，$\mu_0$ 是磁流变液的相对磁导率。

总等效磁阻表示为：

$$
Q = Q_0 + Q_1 + Q_2 + Q_3 + Q_4 \quad (16)
$$

磁感应时间常数表示为（郑等人，2011）：

$$
f = \frac{4\pi^2 N^2 (R_3 + R_2)^2 I}{3 \times 10^{-6} K_n Q} \quad (17)
$$

其中，$N$ 为线圈匝数，$K_n$ 为几何系数，$R_3 = R_1 + L_2\tan u - H_0 - L_0$，$I$ 为电流密度。

3. 仿真分析

在径向阻尼通道的磁流变支座中，通道内的磁通密度随着内径$R_1$的增大而逐渐增加，当内径$R_1$足够大时，通道内的磁通密度趋于饱和。然而，当阻尼通道增加5°倾斜角后，增大倾斜角能够提高锥形阻尼通道内平均磁通密度的饱和点，如图5所示。根据公式(3)和(8)，可得到径向阻尼通道和锥形阻尼通道产生的总压降。锥形阻尼通道的总压降相比径向阻尼通道有所提高，如图6所示。

因此，增大倾斜角u对本文提出的结构具有一定影响。

理想的磁流变支座磁路应能产生足够强的磁场，以在所需的屈服应力范围内激活液体，而无需高电流。

本文中，当电流为1安且磁路的初始结构参数如表1所示时，采用有限元方法分析了结构参数对磁通密度、压降和感应时间的影响。线圈横截面积为28.2（mm²），匝数为250。

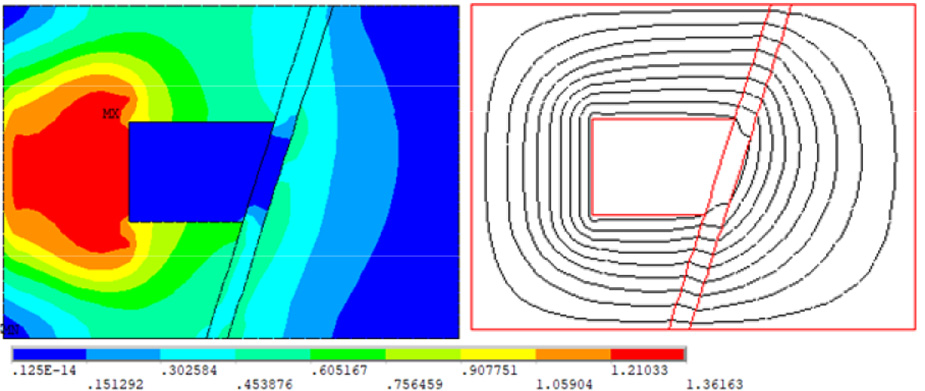
使用ANSYS APDL对磁芯进行分析，划分了四边形网格，并施加了磁力线的平行边界条件。磁路仿真结果如图7所示。根据锥形阻尼通道中磁通密度的分布特性，有效磁阻尼通道由上通道和下通道组成。

3.1. 对磁通强度的影响

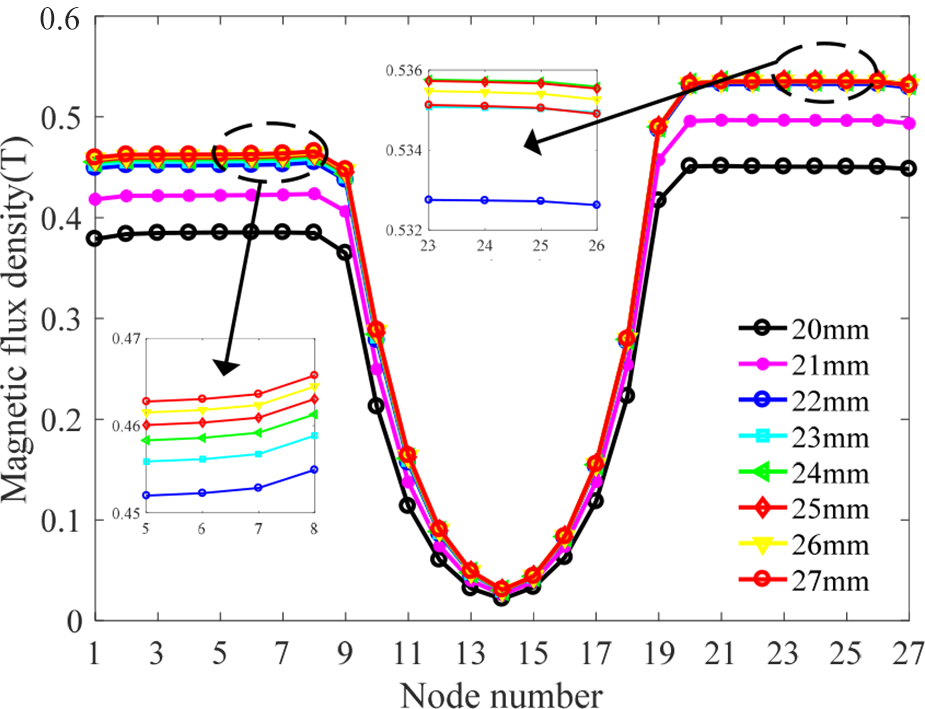
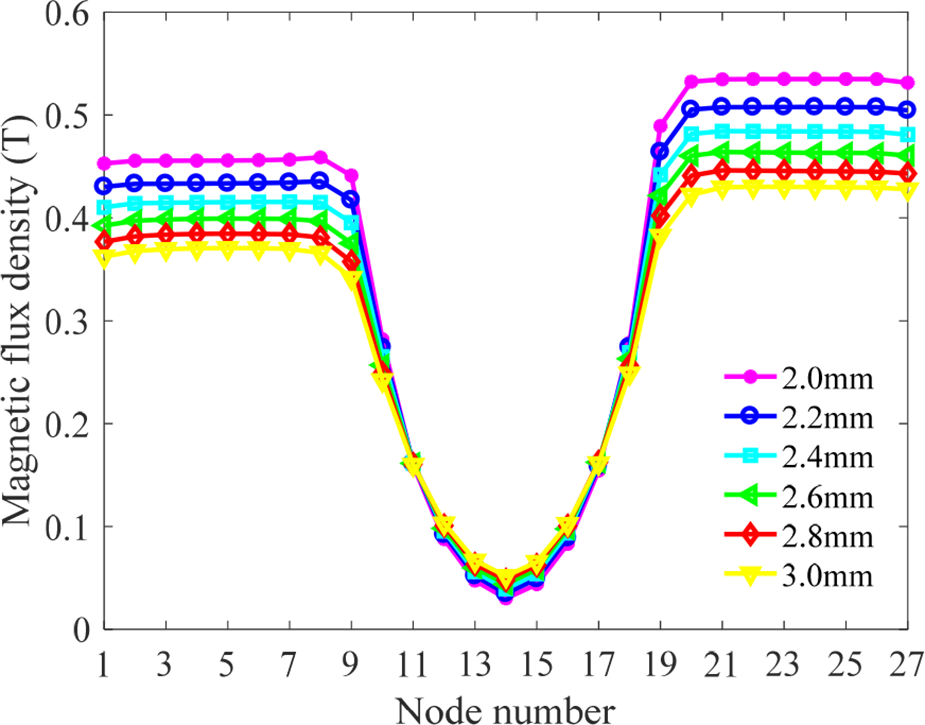
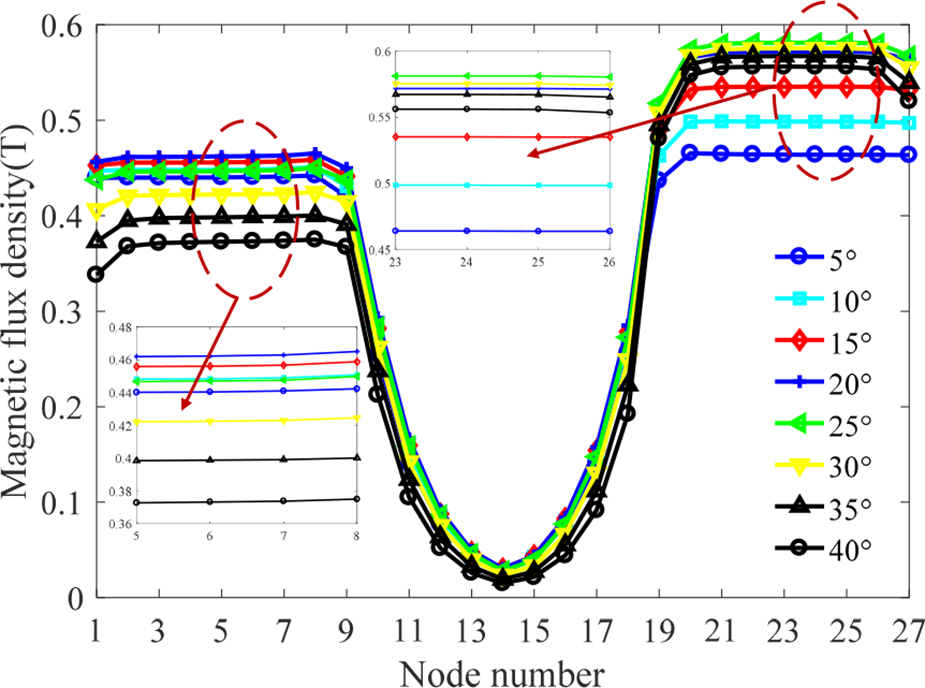
当内径$R_1$ 范围为20–27毫米，阻尼间隙$H_0$ 为2–3毫米，倾斜角$u$为 5°–40°时，分析结果如图8–10所示。

参数	$R_1$ /(mm)	倾斜角 $u$/(°)	$H_0$ /(mm)	$L$/(mm)	$L_1$ /(mm)
Xini	21	15	2	28.8	9.6

表1. 减振器的初始参数

从图8可以看出，阻尼通道的磁通密度随着内径 $R_1$ 的增大而增大。但当内径$R_1$ 增大到22毫米时，磁通密度趋于饱和。图9显示，阻尼通道的磁通密度随着阻尼间隙$H_0$ 的增大而减小。同时，结果表明，磁通密度随着倾斜角$u$的增大先增大后减小，如图10所示。当磁通密度最大时，此时的倾斜角$u$称为突变角。上通道和下通道中磁通密度的突变角分别约为20°和 25°。仿真结果具有一条共同规律：对应于锥形阻尼通道，下通道的磁通密度大于上通道。

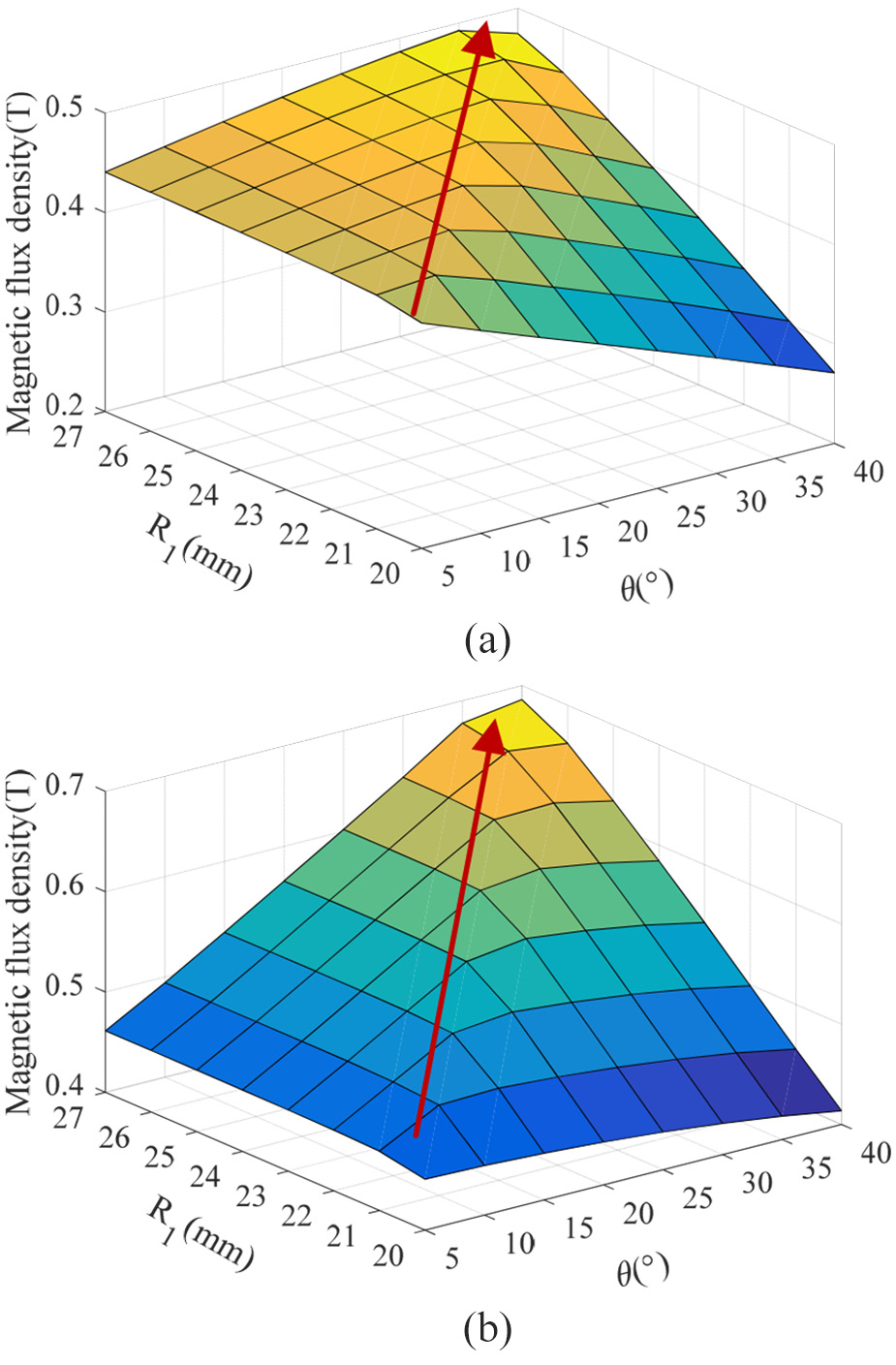
进一步地，当内径$R_1$范围为20–27毫米且倾斜角 $u$为 5°–40°时，对阻尼通道的磁通密度进行了全面分析。图中磁通密度随两个不同结构参数的变化趋势以及红色箭头所示位置即为突变角出现的位置。由图 11(a)和(b)可以看出，随着内径$R_1$ 和倾斜角$u$的增大，突变角呈现逐渐增大的趋势。然而，随着突变角的增加，上通道的磁通密度增长较慢，而下通道的磁通密度则显著增加。

上通道和(b) 下通道)

通过分析上述结构参数对磁通密度的影响，锥形阻尼通道不仅具有传统径向结构的特性，而且有所改进。通过增大内径$R_1$和倾斜角$u$，提高了阻尼通道中平均磁通量密度的饱和点。与传统的径向结构相比，有效缓解了磁流变支座的磁饱和现象。

3.2. 对压降的影响

基于磁流变支座的数学模型，采用与前一节相同的参数分析阻尼通道的压力降。压力降随两个不同结构参数变化的趋势如图所示，其中红色箭头指示的是突变角出现的位置。分析结果如图12–14所示。

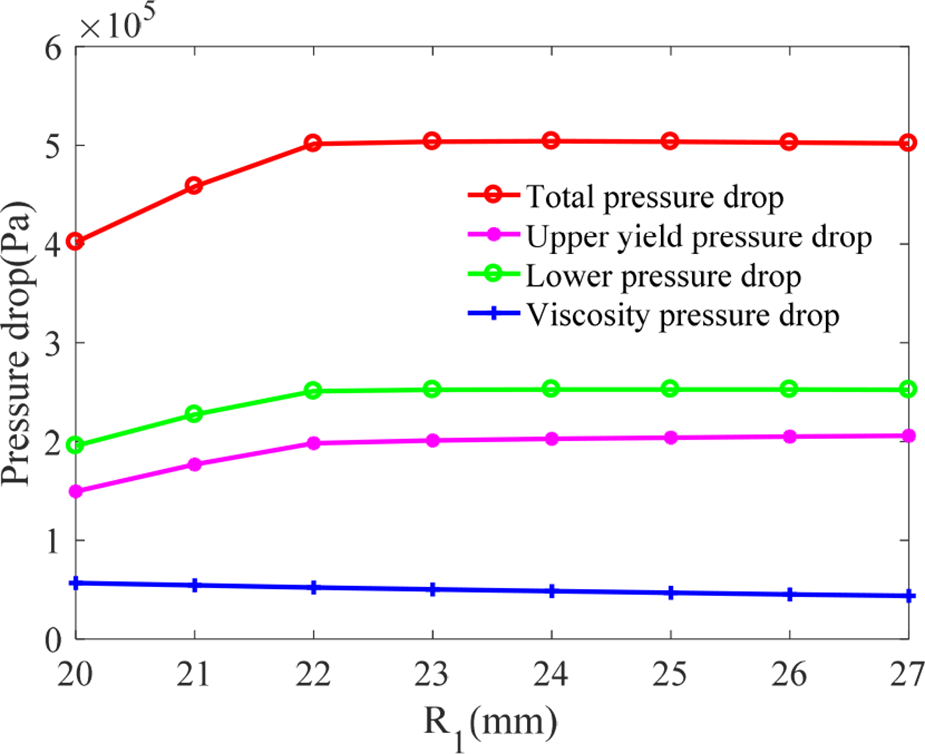
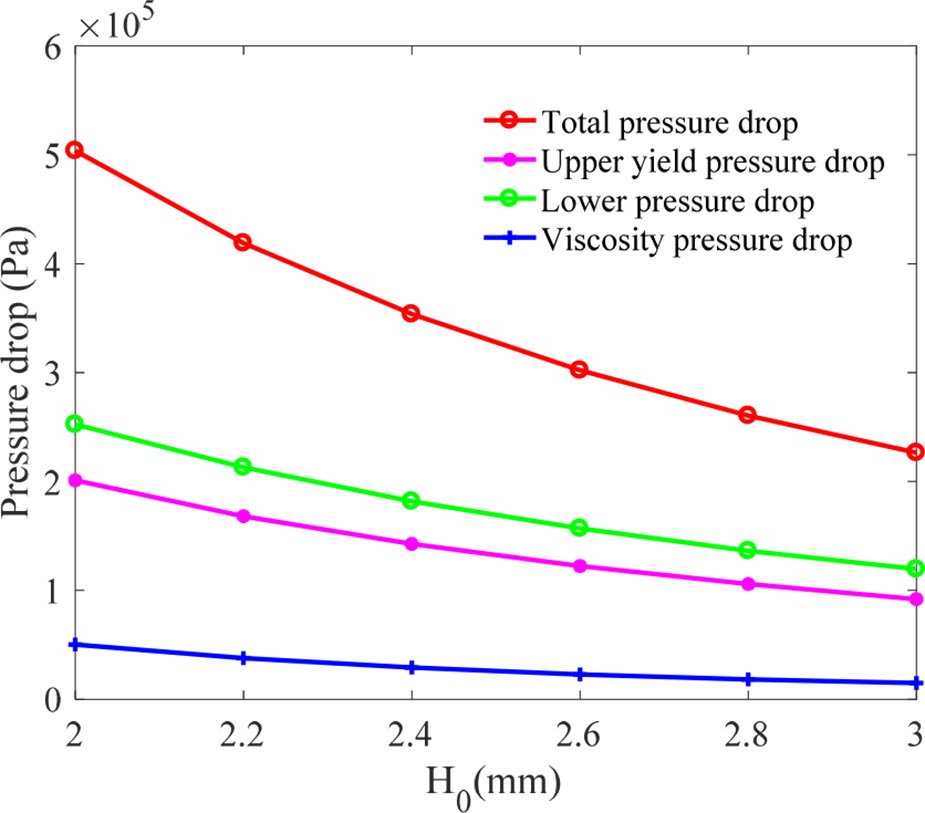
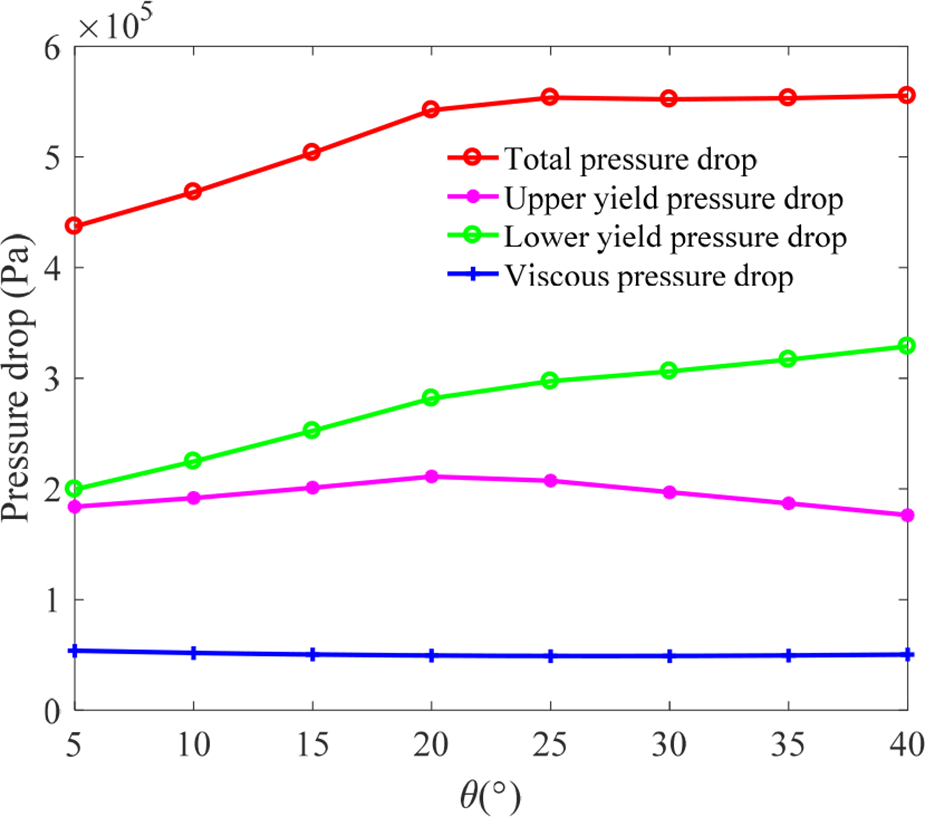
粘性压降随着三个参数的增加而略有减小。总压降和屈服压降随着内径$R_1$的增加而增加，但当$R_1$增加至约22mm时趋于饱和。总压降和屈服压降随着阻尼间隙$H_0$的增加而减小。下通道的总压降和屈服压降随着倾斜角$u$的增加而增加，而上通道的屈服压降则随着倾斜角$u$的增加先增大后减小。仿真结果具有一条共同规律：对应于锥形阻尼通道，下通道的压降大于上通道。

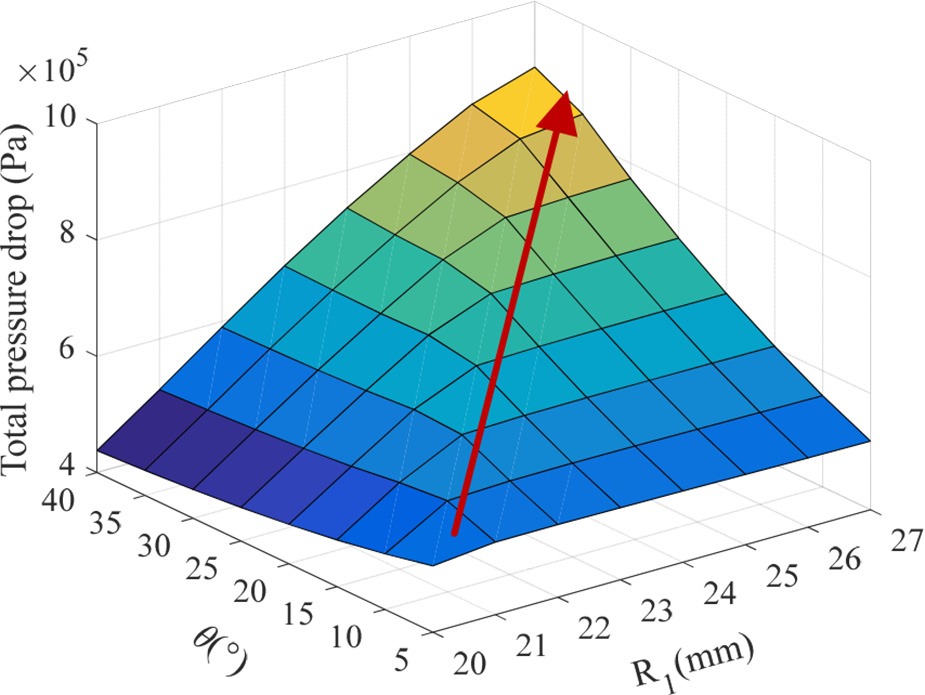
此外，当内径$R_1$为20–27 mm、倾斜角$u$为 5°–40°时，对阻尼通道的压降进行了全面分析。分析结果如图15–17所示。

如图15所示，粘性压降随倾斜角$u$的增大而趋于平缓下降，受内径$R_1$和倾斜角$u$的影响较小。如图16所示，倾斜角$u$和内径$R_1$的变化对屈服压降有较大影响。因此，随着$R_1$的增大，总压降的突变角呈现逐渐增加的趋势，且总压降随突变角的增大而增加，如图17所示。锥形阻尼通道不仅有效缓解了磁通强度过早饱和的问题，还显著提高了磁流变支座的可控性。

3.3. 对感应时间的影响

基于图18所示的磁感应时间模型，分析了结构参数对感应时间的影响。

磁感应时间随着内径$R_1$和倾斜角$u$的增加而增加，同时随着阻尼间隙$H_0$的增加而减小。此外，磁感应时间随着电流密度的增加而逐渐减小。

4. 优化设计

根据几何参数对磁通密度和压降的影响，选择内径 $R_1$、阻尼间隙 $H_0$ 和倾斜角 $u$ 作为优化设计变量。

磁通密度的饱和和突变角对压力有重要影响。同时，设计变量的优化会改变感应时间。因此，磁通密度和感应时间均应处于合理范围内。

约束条件为：

$$
\begin{cases}
20\,\text{ms} \leq f \leq 90\,\text{ms} \
0.3\,\text{T} \leq B_1 \leq 0.6\,\text{T} \
0.3\,\text{T} \leq B_2 \leq 0.6\,\text{T}
\end{cases}
$$

其中，$B_1$ 和 $B_2$ 分别为磁流变液在上通道和下通道中的平均磁通量强度，$f$ 为磁感应时间。

阻尼通道的可控性能要求粘性压降小，而屈服压降大。因此，优化目标函数为：

$$
\min \left( \frac{\Delta P_h}{\Delta P_{hi}}, \frac{\Delta P_{ti}}{\Delta P_t} \right)
$$

其中，$\Delta P_{hi}$为初始粘性压降，$\Delta P_{ti}$为初始屈服压降，$\Delta P_h$和$\Delta P_t$分别为已优化的粘性压降和屈服压降。

为了实现磁路结构的多目标约束优化，通过ISIGHT和ANSYS构建了协同仿真优化平台。利用ANSYS建立磁路结构的参数化模型，同时将仿真结果实时传输至ISIGHT，进行磁路结构优化（黄等人，2014；Zhou和Zhou，2008）。采用带精英策略的非支配排序遗传算法（卢等人，2018）。优化原理如图19所示，多目标优化框架如图20所示。

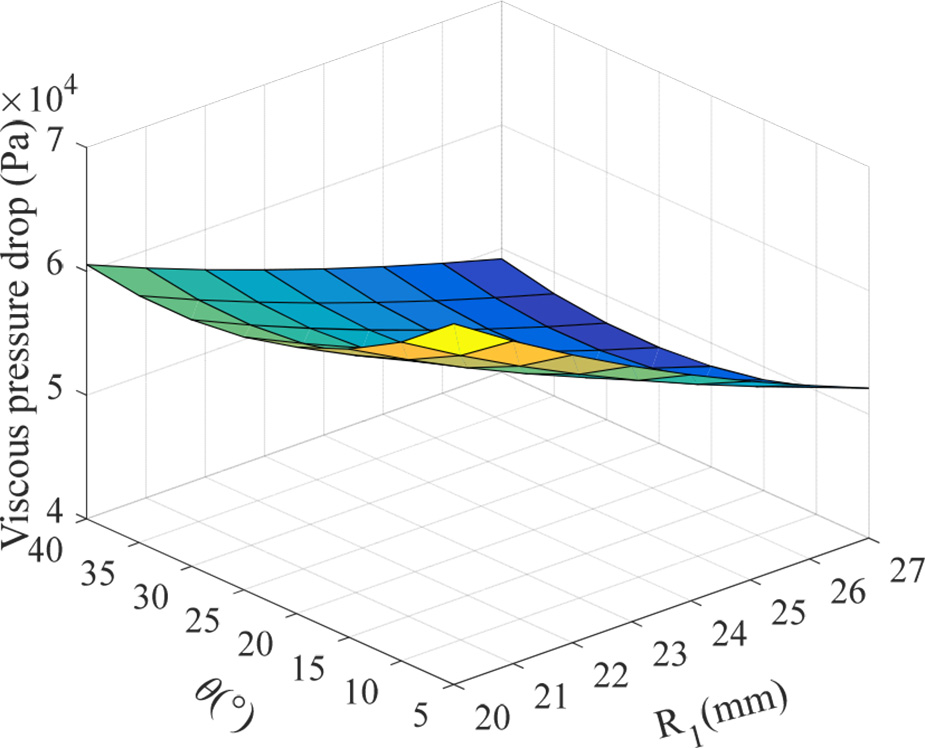
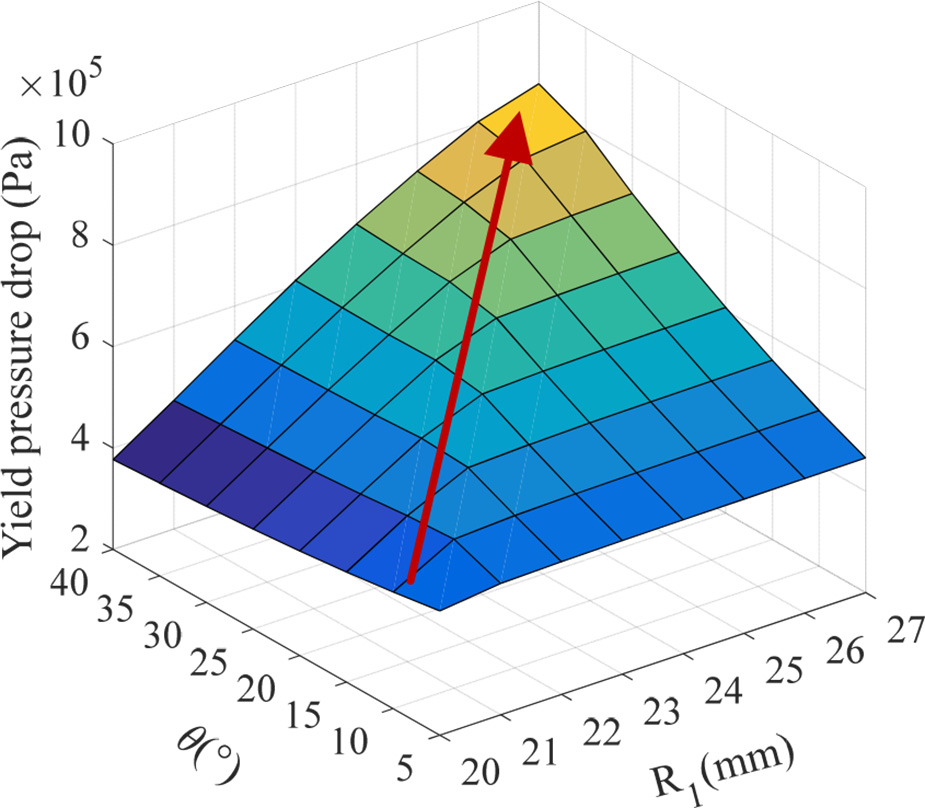
图21显示了迭代优化的粘性压降和屈服压降的收敛曲线。在迭代过程中，粘性压降下降速度最快，而屈服压降逐渐增加。

设计变量	$R_1$ /(mm)	倾斜角 $u$/(°)	$H_0$ /(mm)	$L_1$ /(mm)
优化区间	[18, 26]	[0, 35]	[2, 3]	[7.6, 11.6]
Xini	21	15	2	9.6
Xopt	25.8	21	2.43	10.57

表2. 未优化和已优化的设计变量

约束	$B_1$ /(T)	$B_2$ /(T)	$f$/ (ms)
未优化	0.42	0.49	40.4
已优化	0.43	0.53	66.3

表3. 未优化和已优化的约束

根据表1中磁路的结构尺寸参数，分别对初始模型和已优化模型进行有限元法分析。

阻尼通道未优化和已优化的磁通密度如图22所示。经过200次遗传算法迭代后，节点优化的磁通密度大于未优化的情况。与未优化结构相比，上通道磁流变液的平均磁通密度从0.42 T增加到0.43 T，下通道从0.49 T增加到0.53 T。当电流强度为1 A时，已优化的磁感应时间从40.4 ms增加到66.3 ms。尽管阻尼间隙$H_0$ 减小以及内径$R_1$ 和倾斜角$u$增大导致感应时间增加，但仍处于可接受范围。

设计变量	$P_h$/(kPa)	$P_t$/(kPa)	压力/(kPa)
Xini	61.221	404	465.221
Xopt	35.584	934.6	970.184

表4. 未优化和已优化的目标

压降变化的未优化和已优化结果如表4所示。与未优化结构中，粘性压降从61.221 kPa降低至35.584 kPa，屈服压降从404 kPa增加至934.6 kPa，总压降从465.221 kPa增加至970.184 kPa。

5. 结论

本文提出了流动模式下具有锥形阻尼通道的磁流变支座。首先，根据流体力学建立了阻尼通道的压降模型。然后，通过有限元方法分析了倾斜角$u$和阻尼通道内径$R_1$等关键结构参数对通道内磁通密度和压降的影响。

仿真结果表明，随着内径$R_1$的增大，通道的磁通密度增加并趋于饱和；但在增大阻尼通道的倾斜角$u$后，通道磁通密度的饱和点得到提高。在不同内径$R_1$下，通道磁通密度随倾斜角$u$的增大先增大后减小，且突变角的大小随内径$R_1$ 的增大而增大。通过ISIGHT与ANSYS联合仿真优化平台，对磁路结构进行了已优化，降低了通道内的粘性压降，提高了屈服压降，使支座的可控性更强。