一、串联校正

Gc为校正系统传函,G为系统固定传函,H为反馈系统传函(一般为单位反馈,H=1)。
设计Gc,从而校正系统,使得系统满足性能要求。
二、matlab实现PID校正
例:首先建立传递函数:
G=tf([100],conv([1,0],[0.1,1]))
这里用到matlab里的控制系统设计工具箱,在命令行窗口输入: sisotool
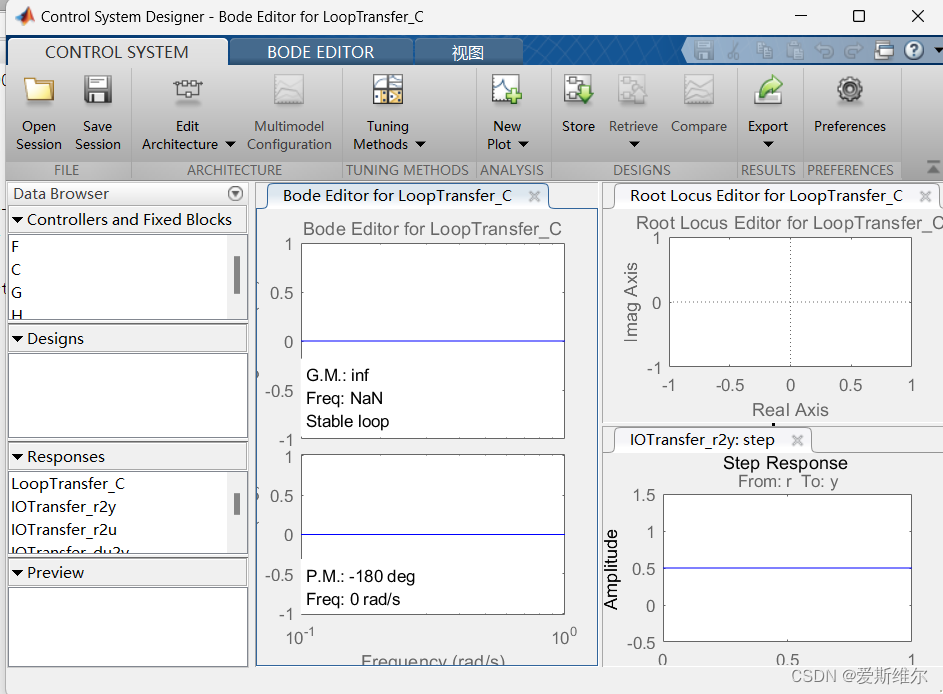
导入传递函数G:


可以在图中看见伯德图和根轨迹图还有阶跃响应的时域图,可以看到在伯德图中,截止频率对应的斜率为-40dB/dec,截止频率为30.8rad/s,可以进行校正,提高截止频率改善快速性,降低斜率到-20dB/dec提高稳定性。
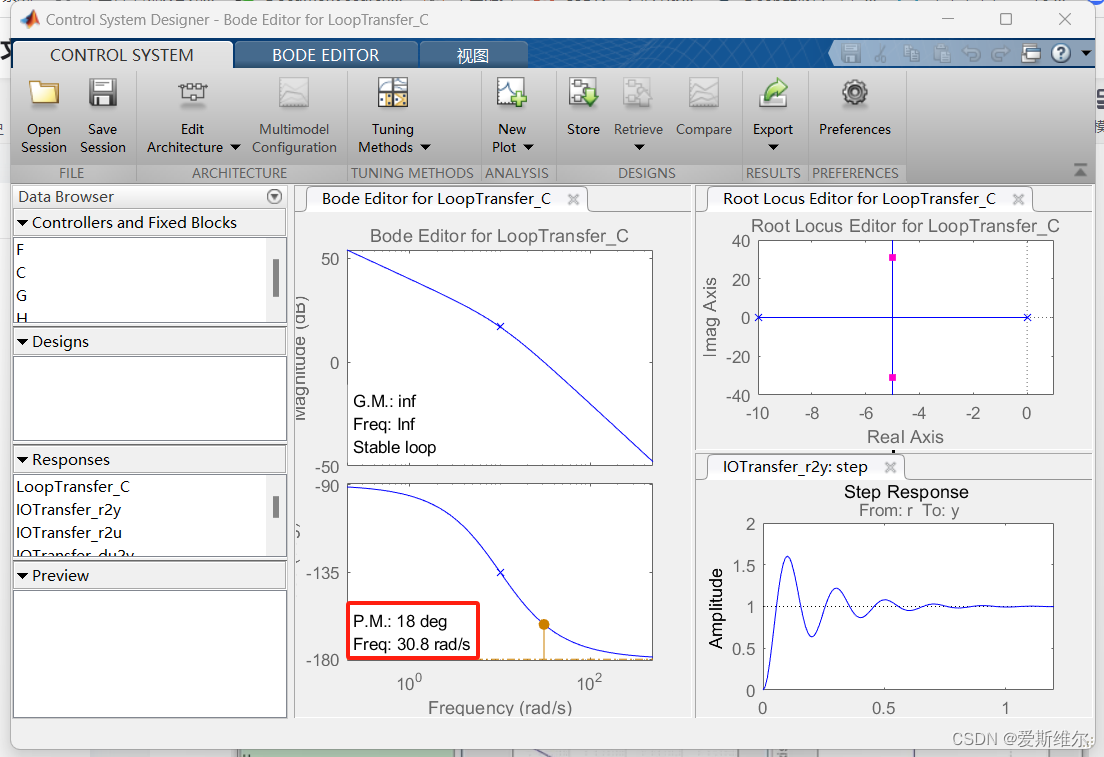
点击store储存,可以发现左栏生成了一个Design1:

为对几个Design进行比较,需要保存Design1的曲线图。故右键Design1,选择compare:
然后打开PID tuning

先使用PD校正器,超前校正

通过调节Response Time和 Transient Behavior,可以生成PD控制器C

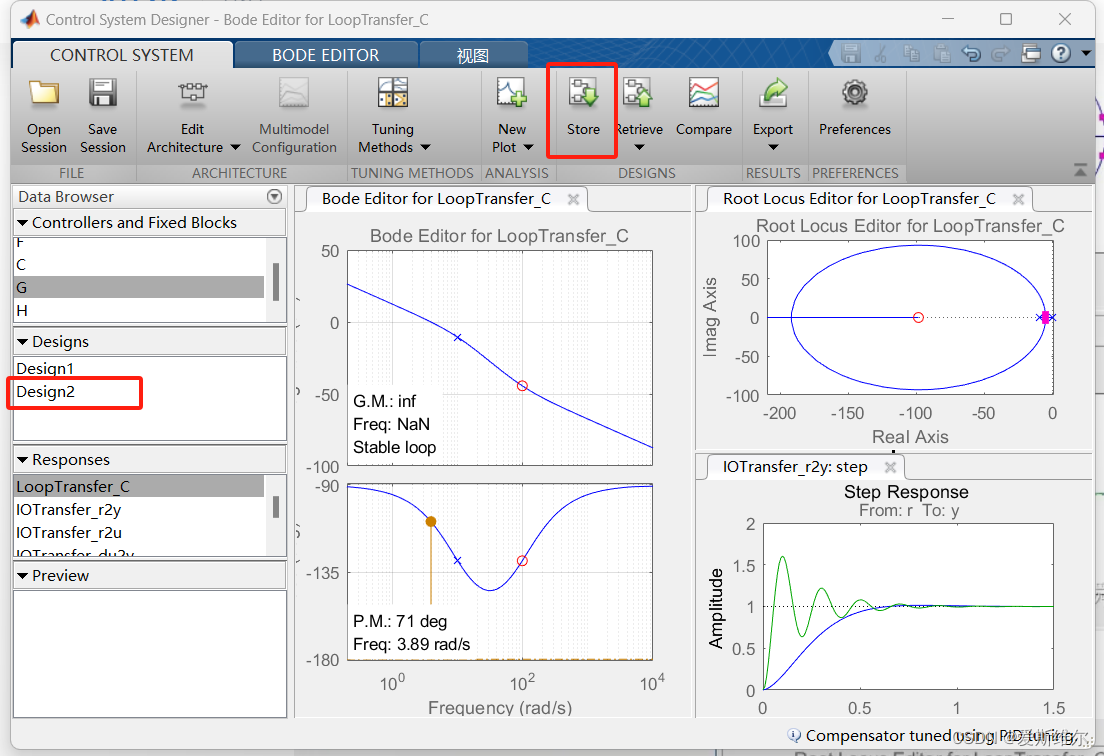
反应在伯德图、根轨迹图和时域分析响应中:可以看到截止频率附近的斜率为-20dB/dec,相角裕度为71°,相对稳定性提高,但反应速度变慢了。

同理点击store对此次设计进行保存,产生 Design2,并进行compare:
再用PI控制(蓝色)

可以看到快速性得到提高,但稳定性,不如PD控制(蓝绿色)

同理store,生成design3,再用PID控制(蓝色),调整参数如下:

可以看到这是一个折中的控制方法:

点击legend可以显示图例,
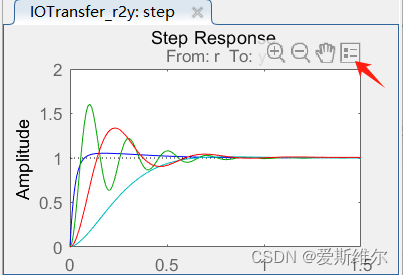
得到如下图所示,Design1为未校正前系统,Design2为PD校正系统,Design3为PI校正系统,蓝色(无标签)为PID校正系统。

然后store,生成Design4(PID校正),鼠标左键点击Design4,左下栏会显示PID相关参数。
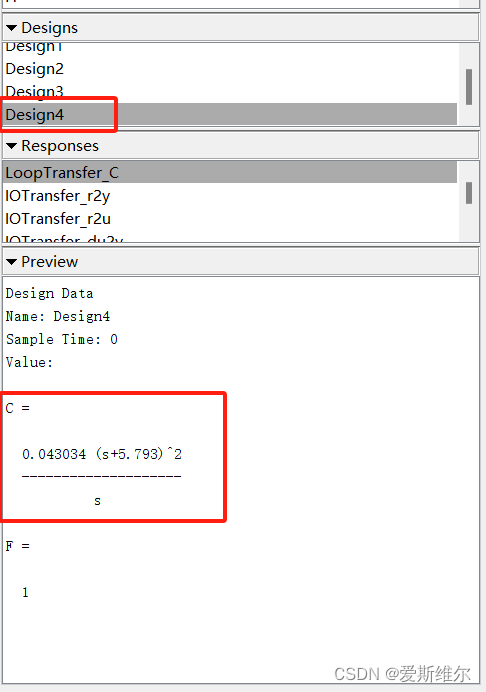
可知,Kp=0.043034*2*5.793,Ki=5.793^2*0.043034,Kd=0.043034
最后,利用simulink搭建仿真模型,并将Kp、Ki、Kd参数输入到PID控制器中。如下图所示分别为校正前系统与校正后系统。

通过示波器可以发现校正后系统输出能较好的跟踪输入,满足性能要求。





 本文介绍了如何使用Matlab中的工具箱进行PID校正,通过例子展示了从PD到PID控制器的调整过程,最终通过Simulink实现系统优化,确保输出能跟踪输入并满足性能需求。
本文介绍了如何使用Matlab中的工具箱进行PID校正,通过例子展示了从PD到PID控制器的调整过程,最终通过Simulink实现系统优化,确保输出能跟踪输入并满足性能需求。

















 7421
7421

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










