自由运动和环境限制-CoCube

之前，两篇：

001：差动驱动机器人轨迹-CoCube

002：迷宫逃离的问题-CoCube

---

分别代表了两种环境下，机器人路径规划的特性。

001：无拘无束的自由空间

如果给定一定的机器人左右轮控制量，机器人可以走出需要的开环曲线。

002：迷宫其实是一种外部环境限制条件下的运动规划，如果仅仅考虑躲避障碍物，那么只需要局部路径规划，但是如果需要考虑类似起点和终点的导航，则还需要全局路径规划，最好还要有一个相对准确的地图，否则容易迷路。

可以简单看一种情况：

这种情况比较简单，只需要穿过中间通道，就可以到达上部分区域。

 

规划效果如下：

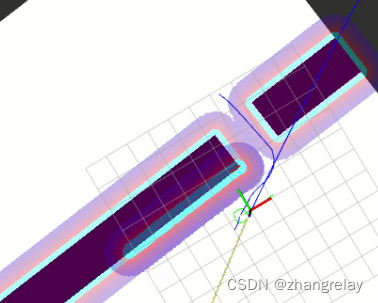
从上部分穿过到下面部分也是类似的。

通道还是比较窄的。

稍微复杂一些情况如下：

 

这些都可以用同一类方式得到解决。

对于求解这一类问题的复杂度是相似的，只不过通常而言地图越复杂需要的计算量越大 

 

这一类迷宫地图，也可以很快得到路径。

ROS1云课→21可视化工具rviz中的A*

从上图到下图：

---

于是，会发现，从：

到：

 ROS1云课→29如何借助导航实现走迷宫机器人

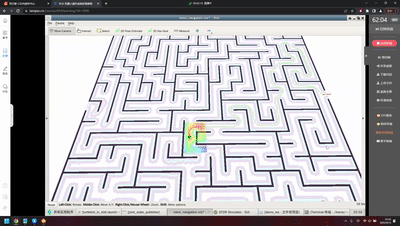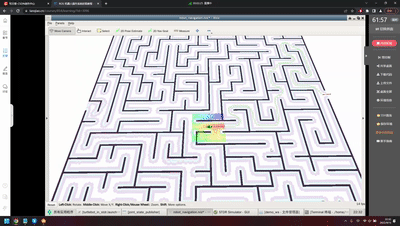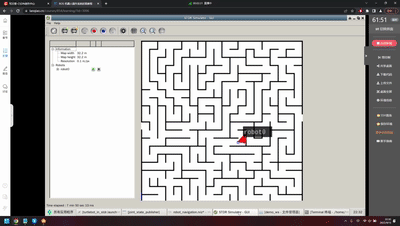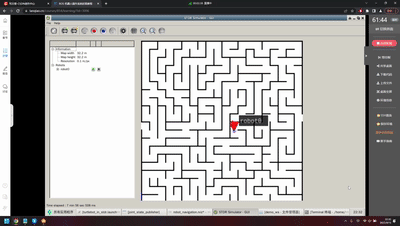
循序渐进的学习和研究是非常重要的。

它们之间只隔着一层思维上的屏障，突破就能完全掌握其应用的。 

---

简单小结一下：

无障碍物空间，机器人自由运动，控制输入直接反映到空间位置和姿态的变化。

有障碍物空间，机器人运动受到环境约束，触碰到障碍物的输入都是无效的，需要在算法上进行判定，避免这种情况的出现，这是开环控制无法解决的问题啦。

怎么办？

需要闭环发力^_^ 

---