散列表查找（哈希表）

一、概述：

散列技术：散列技术是一种通过哈希函数（散列函数）将关键字（Key）映射到存储位置的方法，目的是快速定位数据。其核心思想是将数据的存储位置与关键字建立直接关联，从而实现高效的查找、插入和删除操作。

散列表（哈希表）：散列表是一种基于散列技术实现的数据结构，它通过哈希函数将关键字映射到数组的某个位置（槽，Slot），从而实现快速访问。

二、构造方法：

除留取余法：这是最常用的构造方法，对关键字取模，求出余数，让余数作为散列地址

公式：【f(key)=key%p(p<=散列表的长度)】

三、处理冲突的方法：

1、开放地址法：

当发生冲突时，通过某种规则寻找下一个空槽。常见的开放地址法有：

• 线性探测（Linear Probing）：

  • 公式：f_i(key) = (f(key) + i) % m（i=1,2,3...）
  • 示例：
    • 散列表长度 m=10，p=7，处理 29 和 15 的冲突：
      • 29 初始地址为 1（冲突），探测下一个位置：(1+1)%10=2（空槽，存入位置 2）。
  • 问题：容易形成 “聚集”（Cluster），导致后续冲突频繁。

• 二次探测（Quadratic Probing）：

  • 公式：f_i(key) = (f(key) + i²) % m（i=1,2,3...）
  • 示例：
    • 冲突时，依次探测位置f(key)+1², f(key)+2², f(key)+3²...。
  • 优点：减少线性探测的聚集问题。

• 伪随机探测：

  • 公式：f_i(key) = (f(key) + random(i)) % m（random (i) 为随机数序列）。

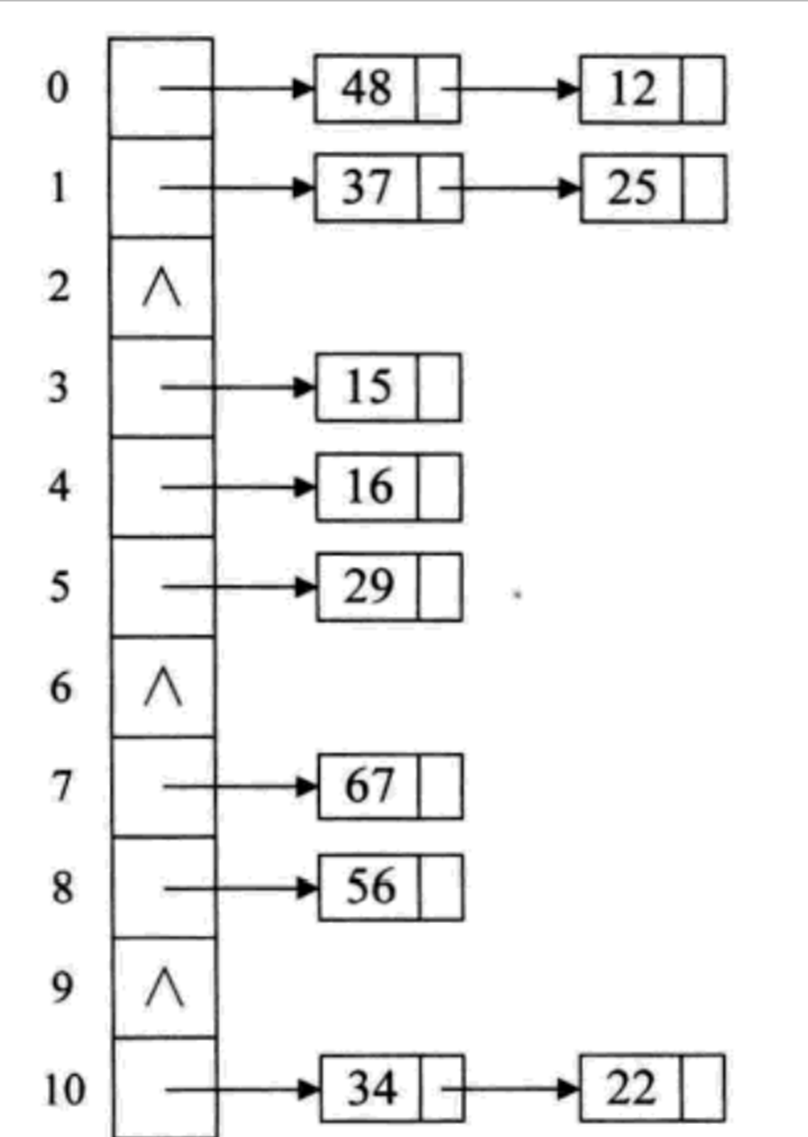
2、链地址法：将所有哈希地址相同的元素存储在同一个链表中。哈希表每个位置对应一个链表头节点，冲突的元素插入到对应链表中。

 

 四、参考代码：

#include<iostream>
#define NULLKEY -32768  // 定义空键标记，用于初始化哈希表，表示该位置未存储数据

using namespace std;

// 哈希函数：使用除留取余法将关键字映射到哈希表位置
// 此处固定使用11作为模数
int Hash(int key){
    int add;
    add=key%11;
    return add;
}

// 插入函数：将关键字插入哈希表
// 参数：h-哈希表指针，key-待插入的关键字
void InsertHash(int* h,int key){
    int add=Hash(key);  // 计算初始哈希位置

    // 线性探测处理冲突：如果当前位置已被占用，则尝试下一个位置
    while(h[add]!=NULLKEY){   
        add=(add+1)%11;     
    }
    h[add]=key;  // 找到空位置后插入关键字
}

// 查找函数：在哈希表中查找指定关键字
// 参数：h-哈希表指针，key-待查找的关键字
// 返回值：若找到返回关键字位置，未找到返回-1
int SearchHash(int* h,int key){
    int add=Hash(key);  // 计算初始哈希位置
    int start=add;      // 记录初始位置，用于判断是否遍历完整个哈希表

    // 线性探测查找：如果当前位置不是目标关键字，则继续查找下一个位置
    while(h[add]!=key){
        add=(add+1)%11; 
        // 如果回到初始位置，说明已遍历完整个哈希表，未找到目标关键字，返回-1 
        if(add==start)    
            return -1;
    }
    return add;  // 找到目标关键字，返回其位置
}

int main(){
    int t;
    cin>>t;  // 输入测试用例数量
    
    while(t--){
        int m,n,i;
        int *h;
        cin>>m>>n;    // m为哈希表大小，n为关键字数量
        
        // 创建哈希表并初始化为NULLKEY
        h=new int[m];
        for(i=0;i<m;i++){
            h[i]=NULLKEY;
        }
        
        // 输入n个关键字并插入哈希表
        for(i=0;i<n;i++){
            int key;
            cin>>key;
            InsertHash(h,key);
        }
        
        // 处理k次查询
        int k;
        cin>>k;       
        for(i=0;i<k;i++){
            int key;
            cin>>key;
            
            cout<<SearchHash(h,key)<<endl;  
        }
        
        delete[] h;   
    }
    
    return 0;
}