111. 二叉树的最小深度

111. 二叉树的最小深度

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

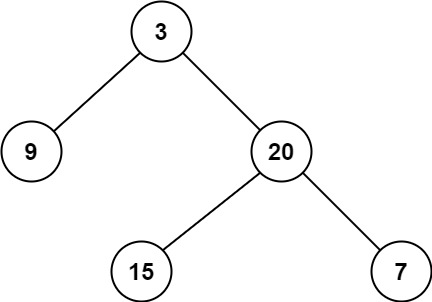
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 10^5] 内
• -1000 <= Node.val <= 1000

思路：

看完了上篇104.二叉树的最大深度 ，再来看看如何求最小深度。

直觉上好像和求最大深度差不多，其实还是差不少的。

本题依然是前序遍历和后序遍历都可以，前序求的是深度(因为是从根节点开始初始，每进入下一层，深度+1），后序求的是高度（因为要一直到叶子节点为止，所以可以先处理叶子节点，然后回溯回去回到根节点）。

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。

以下讲解中，遍历顺序上依然采用后序遍历（因为要比较递归返回之后的结果，本文我也会给出前序遍历的写法）。

本题还有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解，如图：

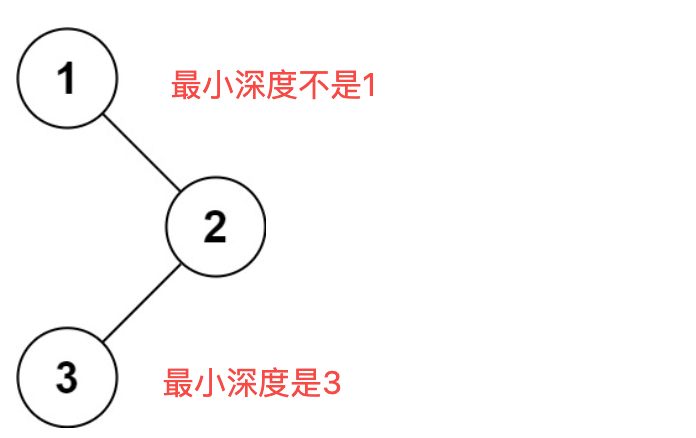
这就重新审题了，题目中说的是：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。

什么是叶子节点，左右孩子都为空的节点才是叶子节点！

递归法

递归三部曲：

1. 确定递归函数的参数和返回值
   参数为要传入的二叉树根节点，返回的是int类型的深度。

代码如下：

func getDepth(root *TreeNode) int {}

2. 确定终止条件
   终止条件也是遇到空节点返回0，表示当前节点的高度为0。

代码如下：

if root == nil {
        return 0
  }

3. 确定单层递归的逻辑
   这块和求最大深度可就不一样了，一些同学可能会写如下代码：

  leftDepth := getDepth(root.Left) // 左
  rightDepth := getDepth(root.Right) // 右
 // 根（遍历到根时就是具体的处理逻辑，遍历到左右节点时则是递归）
  curNodeDepth = min(leftDepth,rightDepth) + 1 
  return curNodeDepth

这个代码就犯了此图中的误区：

如果这么求的话，没有左孩子的分支会算为最短深度。

所以:

• 如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

• 反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。

• 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

代码如下：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    // 左右子树都不为空的时候，当前节点的深度为左右子树较小深度+1
    if root.Left != nil && root.Right != nil {
    	leftDepth := minDepth(root.Left) // 左
    	rightDepth := minDepth(root.Right) // 右
    	depth := min(leftDepth,rightDepth) + 1 // 根
        return depth
    }
    // 通过上述if，则一定是左或右子树有一个为空
    if root.Left != nil {
        return minDepth(root.Left) + 1
    }
    // 通过了上面两个if 那一定是右子树不为空
    return minDepth(root.Right) + 1
}


func min(a,b int) int {
    if a < b {
        return a
    }

    return b
}

遍历的顺序为后序（左右中），可以看出：求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。

精简之后代码如下：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    // 左右子树都不为空的时候，当前节点的深度为左右子树较小深度+1
    if root.Left != nil && root.Right != nil {
        return min(minDepth(root.Left),minDepth(root.Right)) + 1
    }
    // 通过上述if，则一定是左或右子树有一个为空
    if root.Left != nil {
        return minDepth(root.Left) + 1
    }
    // 通过了上面两个if 那一定是右子树不为空
    return minDepth(root.Right) + 1
}


func min(a,b int) int {
    if a < b {
        return a
    }

    return b
}

精简之后的代码根本看不出是哪种遍历方式，所以依然还要强调一波：如果对二叉树的操作还不熟练，尽量不要直接照着精简代码来学。

前序遍历的方式：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    
    res := math.MaxInt32
    dfs(root,1,&res)
    return res
}

func dfs(root *TreeNode,depth int ,res *int) {
    if root == nil {
        return 
    }
    // 中，处理逻辑：判断是不是叶子结点，更新最小深度
    if root.Left == nil && root.Right == nil {
        if depth < *res {
            *res = depth
        }
    }

    if root.Left != nil { // 左
        dfs(root.Left,depth + 1,res)
    }

    if root.Right != nil { // 右
        dfs(root.Right,depth + 1,res)
    }
}

迭代法

相对于104.二叉树的最大深度 ，本题还可以使用层序遍历的方式来解决，思路是一样的。

需要注意的是，只有当左右孩子都为空的时候，才说明遍历到最低点了。如果其中一个孩子不为空则不是最低点

代码如下：（详细注释）

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    
    // 层序遍历，遍历到第一个左右孩子为空的节点（叶子节点）所在层，就是最小深度
    queue := make([]*TreeNode,0)
    queue = append(queue,root)
    depth := 0
    for len(queue) > 0 {
        queueSize := len(queue)
        depth++
        for i := 0;i < queueSize;i++ {
            curNode := queue[0]
            queue = queue[1:]
            // 遍历到了第一个叶子节点所在的层，当前层就是最小深度
            if curNode.Left == nil && curNode.Right == nil {
                return depth
            }
            if curNode.Left != nil {
                queue = append(queue,curNode.Left)
            }
            if curNode.Right != nil {
                queue = append(queue,curNode.Right)
            }
        }
    }
    
    return depth
}