前言
两幅视图存在两个关系:第一种,通过对极几何,一幅图像上的点可以确定另外一幅图像上的一条直线;另外一种,通过上一种映射,一幅图像上的点可以确定另外一幅图像上的点,这个点是第一幅图像通过光心和图像点的射线与一个平面的交点在第二幅图像上的影像。第一种情况可以用基本矩阵来表示,第二种情况则用单应矩阵来表示。而本质矩阵则是基本矩阵**的一种特殊情况,是在归一化图像坐标系下的基本矩阵。
一 本质矩阵如何推导
推导过程梳理如下:


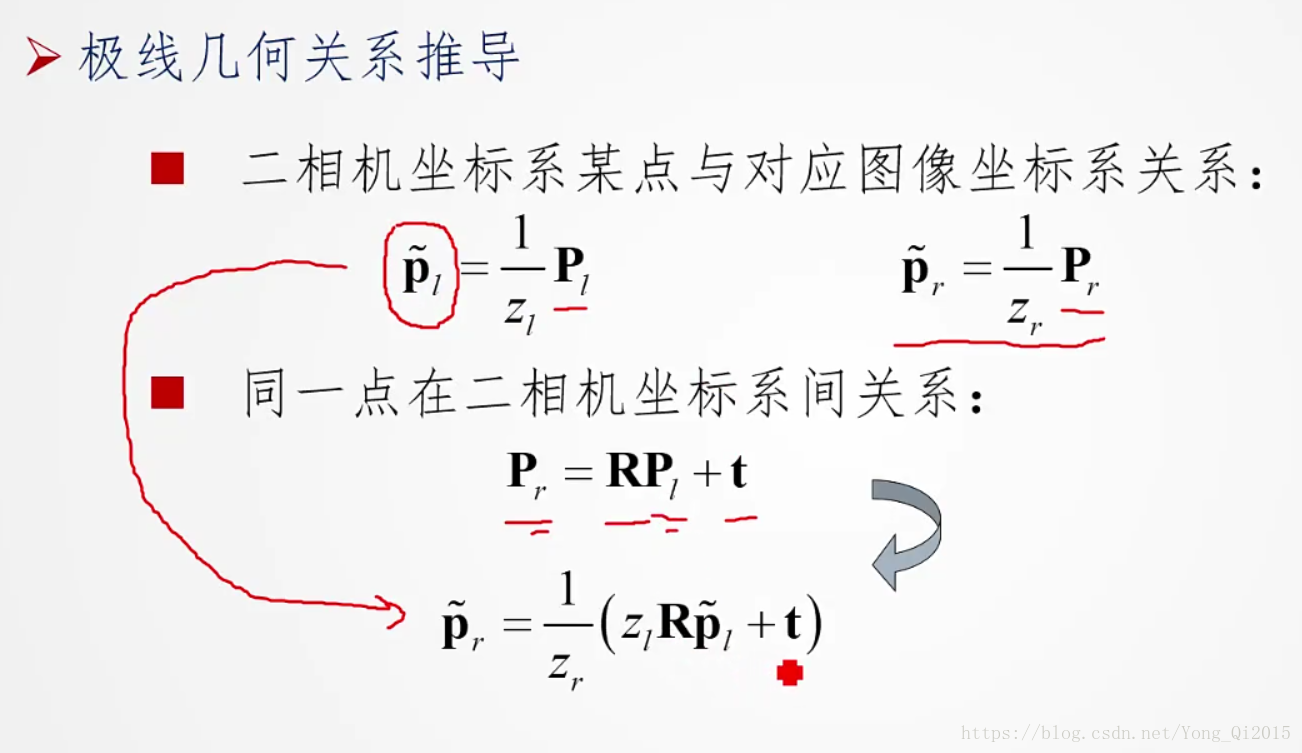
两幅视图存在两个关系:第一种,通过对极几何,一幅图像上的点可以确定另外一幅图像上的一条直线;另外一种,通过上一种映射,一幅图像上的点可以确定另外一幅图像上的点,这个点是第一幅图像通过光心和图像点的射线与一个平面的交点在第二幅图像上的影像。第一种情况可以用基本矩阵来表示,第二种情况则用单应矩阵来表示。而本质矩阵则是基本矩阵**的一种特殊情况,是在归一化图像坐标系下的基本矩阵。
推导过程梳理如下:



 2320
2320
 1393
1393
 973
973
 421
421
 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


